
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Стратегия поиска. Стратегия метода Ньютона-Рафсона [ Newton - Raphson ] состоит в построении последовательности точек { xk}
|
|
Стратегия метода Ньютона-Рафсона [ Newton - Raphson ] состоит в построении последовательности точек { xk }, k = 0, 1,..., таких, что f (xk + 1) < f (xk), k = 0, l,... Точки последовательности вычисляются по правилу
xk + 1 = xk – tkH – 1(xk) ∇ f (xk), k = 0, 1,..., (7.4)
где х 0задается пользователем, а величина шага tk определяется из условия
Стратегия метода Ньютона [ Newton I.] состоит в построении последовательности точек { xk }, k = 0, 1,..., таких, что f (xk + 1) < f (xk), k = 0, l,... Точки последовательности вычисляются по правилу
xk + 1 = xk + dk, k = 0, 1,..., (7.4)
где х 0— задается пользователем, а направление спуска dk определяется для каждого значения k по формуле
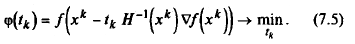
Задача (7.5) может решаться либо аналитически с использованием необходимого условия минимума 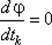 с последующей проверкой достаточного условия
с последующей проверкой достаточного условия 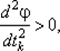 либо численно как задача.
либо численно как задача.

где интервал [ a, b ] задается пользователем.
Если функция φ (tk) достаточно сложна, то возможна ее замена полиномом P (tk) второй или третьей степени и тогда шаг tk может быть определен из условия 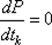 при выполнении условия
при выполнении условия 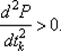
При численном решении задачи определения величины шага степень близости найденного значения tk к оптимальному значению 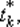 удовлетворяющему условиям
удовлетворяющему условиям 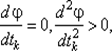 зависит от задания интервала [ a, b ] и точности методов одномерной минимизации.
зависит от задания интервала [ a, b ] и точности методов одномерной минимизации.
Построение последовательности { х k } заканчивается в точке х k, для которой || ∇ f (xk) || < ε 1, где ε 1— заданное число, или при k ≥ М (M — предельное число итераций), или при двукратном, одновременном выполнении двух неравенств || xk +1 – xk || < ε 2, | f (xk +1) – f (xk) | < ε 2, где ε 2— малое положительное число. Вопрос о том, может ли точка х k рассматриваться как найденное приближение искомой точки минимума, решается путем проведения дополнительного исследования, которое описано ниже.