
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Резонанс в последовательной цепи (резонанс напряжений)
|
|
Под резонансом в электрической цепи понимают такое ее состояние, когда ток и напряжение совпадают по фазе и вся цепь ведет себя как чисто активная (рис. 1.18). 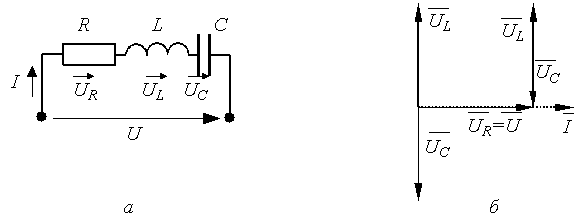
Рис. 1.18. Резонансная цепь (а) и векторная диаграмма при резонансе (б)
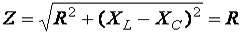 (из определения резонанса);
(из определения резонанса);
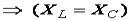 (условие резонанса напряжений);
(условие резонанса напряжений);
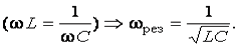
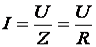 ;
;
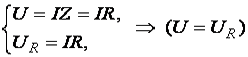 ;
;
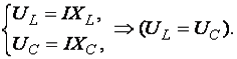
Если 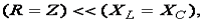 то
то 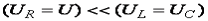 , т.е. напряжение на реактивных элементах цепи может быть больше напряжения, подводимого ко всей цепи.
, т.е. напряжение на реактивных элементах цепи может быть больше напряжения, подводимого ко всей цепи.
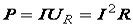 ,
,
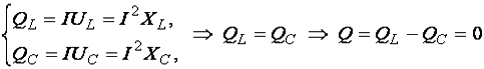 ,
,
т.е. цепь из сети реактивную мощность не потребляет и в сеть её не отдает;
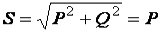 ;
;
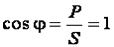 .
.
В момент резонанса происходит обмен энергии между L и C. Из сети реактивная мощность не потребляется и в сеть не отдается, следовательно, цепь ведет себя как чисто активная.
35. Резонанс токов возникает в цепях переменного тока состоящих из источника колебаний и параллельного колебательного контура. Резонанс тока это увеличение тока проходящего через элементы контура при этом увеличение потребление тока от источника не происходит.
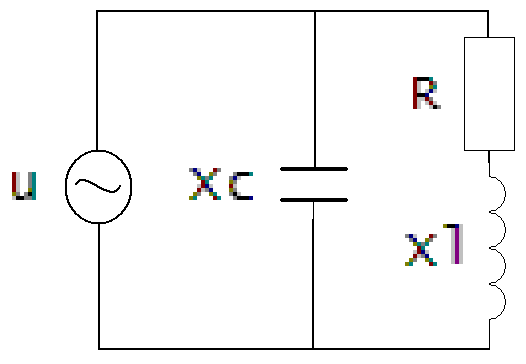
Рисунок 1 — параллельный колебательный контур
Для возникновения резонанса токов необходимо чтобы реактивные сопротивления емкости и индуктивности контура были равны. А также частота собственных колебаний контура была равна частоте колебаний источника тока.
Во время наступления резонанса токов или так называемого параллельного резонанса напряжение на элементах контура остается неизменным и равным напряжению, которое создает источник. Поскольку он подключен параллельно контуру. Потребление тока от источника будет минимально, так как сопротивление контура при наступлении резонанса резко увеличится.
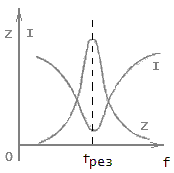
Рисунок 2 — зависимость полного сопротивления контура и тока от частоты
Сопротивление колебательного контура относительно источника колебаний будет иметь чисто активный характер. То есть не будет, провялятся ни емкостная, ни индуктивная составляющая. И сдвиг фаз между током и напряжением будет отсутствовать.
В тоже время ток через индуктивность будет отставать от напряжения на 90 градусов. А ток в емкости буде опережать напряжение на те же 90 градусов. Таким образом, токи в реактивных элементах контура будут сдвинуты по фазе на 180 градусов друг относительно друга.
В итоге получается, что в параллельном колебательном контуре протекают реактивные токи достаточно большой величины, но при этом он от источника напряжения потребляет малый ток необходимый лишь для компенсации потерь в контуре. Эти потери обусловлены наличием активного сопротивления сосредоточенного по большей части в индуктивности.
Источник затрачивает энергию при включении, заряжая емкость. Далее энергия, накопленная в электрическом поле конденсатора, переходит в энергию магнитного поля индуктивности. Индуктивность возвращает энергию емкости, и процесс повторяется снова. Источник напряжения лишь должен компенсировать потери энергии в активном сопротивлении контура.
31.
1. Метод контурных токов используется обычным способом, однако, к напряжениям самоиндукции на катушках добавляем напряжения взаимной индукции (типа 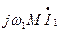 ). Контурные токи желательно выбирать так, чтобы на каждую катушку приходился свой контурный ток.
). Контурные токи желательно выбирать так, чтобы на каждую катушку приходился свой контурный ток.
а. Пример

|
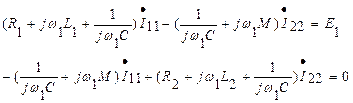
Примечание: Перед М берем " -", так как имеем встречное включение
| б. Пример |
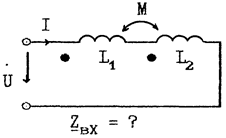
|
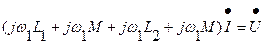
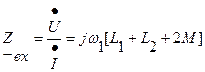
Примечание: Перед М берем " +", так как имеем согласное включение
2. Развязка индуктивных связей используется для замены индуктивно связанных катушек с одним общим зажимом на три обычных индуктивности.
 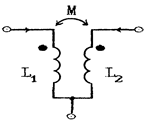
|
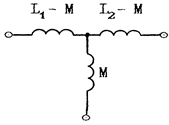
|
Примечание: При другом расположении одноименных зажимов следует поменять всюду знак перед М.
3. Использование вместо реальных трансформаторов эквивалентных схем с идеальными трансформаторами часто упрощает расчет.
28 В электротехнике и электронике широко используются устройства, которые содержат индуктивные катушки, связанные общими магнитными потоками. Примером такого устройства является трансформатор, который служит для преобразования уровней переменных напряжений и токов и для согласования сопротивлений отдельных участков цепи.
Физическая картина заключалась в следующем: переменный ток 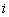 , протекая по виткам катушки (рис. 8.1, а) создает переменный магнитный поток
, протекая по виткам катушки (рис. 8.1, а) создает переменный магнитный поток 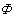 , который сцепляясь с витками
, который сцепляясь с витками 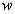 катушки, обуславливает появление ЭДС самоиндукции eL, противодействующей по закону Ленца изменению потокосцепления
катушки, обуславливает появление ЭДС самоиндукции eL, противодействующей по закону Ленца изменению потокосцепления 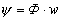 , то есть
, то есть
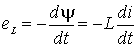 ,
,
где 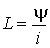 - индуктивность, численно равная отношению потокосцепления самоиндукции к току, его обуславливающему.
- индуктивность, численно равная отношению потокосцепления самоиндукции к току, его обуславливающему.
Теперь рассмотрим явление взаимоиндукции, то есть явление наведения ЭДС в одной электрической цепи при изменении в ней потокосцепления, вызванного изменением тока в другой электрической цепи. Для этого проанализируем картину магнитного поля индуктивно-связанных катушек (рис. 8.1, б).
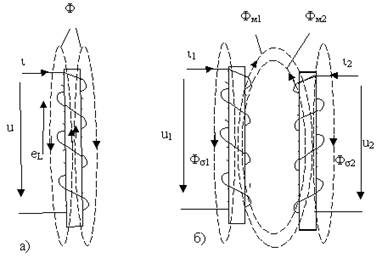
Рис.8.1 - К определению индуктивно связанных цепей
Связь магнитных потоков катушек обусловливает их индуктивную связь. Взаимно индуктивная связь проявляется в наведении ЭДС (называемой ЭДС взаимоиндукции) в одной катушке при изменении тока в другой близко расположенной катушке.
Цепи, в которых наводятся ЭДС взаимоиндукции, называют индуктивно связанными цепями.
Рассмотрим цепь, состоящую из двух индуктивных катушек, намотан-ных на общий сердечник (рисунок 8.2). На схеме обозначено: L 1, R 1 и L 2, R 2 – индуктивности и активные сопротивления первой и второй катушек; М – взаимная индуктивность.
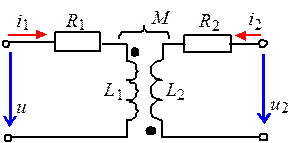
Рисунок 8.2 ‑ Схема замещения двух, индуктивно связанных,
катушек
Взаимная индуктивность M зависит от индуктивностей обоих контуров и их взаимного расположения, поэтому при некоторой ориентации даже близко расположенных контуров взаимная индуктивность может быть равной нулю. Единица измерения взаимной индуктивности и индуктивности одинакова − генри.
Каждая из катушек пронизывается двумя магнитными потоками: потоком самоиндукции, вызванным собственным током, и потоком взаимоиндукции, вызванным током другой катушки.
В соответствии с принципом наложения потокосцепление первой катушки
 (8.1)
(8.1)
Потокосцепление второй катушки
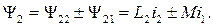 (8.2)
(8.2)
Значения взаимной индуктивности М в выражениях (8.1) и (8.2) одинаковы и не могут превышать среднего геометрического из значений и: L1 и L2:
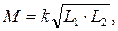
где k – коэффициент связи, характеризующий магнитную связь между катушками. Его величина равна отношению взаимной индуктивности и среднего геометрического значения индуктивностей обеих катушек:
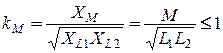
где XL 1 и XL 2 – индуктивные сопротивления катушек.
В пределе, когда магнитный поток одной катушки полностью пронизывает витки другой, k =1. При отсутствии магнитной связи k =0.
Знаки слагаемых в (8.1) и (8.2) зависят от взаимного направления магнитных потоков катушек. В свою очередь, направления магнитных потоков зависят как от направления токов в катушках, так и от их взаимного расположения.
Если катушки включены таким образом, что потоки складываются, то такое включение называют согласным. Если магнитные потоки направлены навстречу друг другу, то катушки включены встречно.
При согласном направлении токов в двух индуктивно связанных ка-тушках зажимы этих катушек, относительно которых токи направлены одинаково, называют одноименными. Одноименные зажимы принято обозначать точками или звездочками.
Физически направления магнитных потоков в катушках определяется правилом правоходового винта. Например, потоки Фм1 и Фм2 на рис. 8.3, а направлены противоположно при заданных направлениях токов i 1 и i 2, т.е. катушки включены встречно. Однако, если бы эти токи были ориентированы одинаково относительно зажимов соответственно 1 и 4, то потоки были бы направлены одинаково. Следовательно, эти зажимы можно считать одноименными.
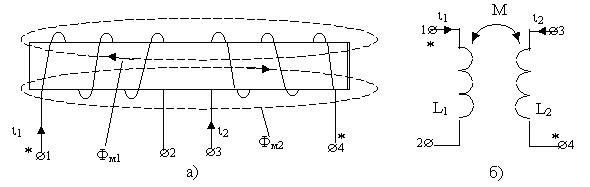
Рисунок 8.3 - Встречное включение катушек
На рис. 8.3, б изображена эл. схема, соответствующая рисунку 8.3, а, где
наличие индуктивной связи между катушками показано дугой с стрелками, над которой стоит символ " М", а одноименные зажимы помечены символами (*).
Определим напряжения на зажимах индуктивно связанных катушек на основе второго закона Кирхгофа:
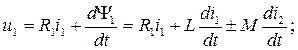 (8.3)
(8.3)
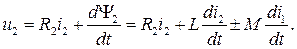 (8.4)
(8.4)
Основной формой расчета цепей синусоидального тока является метод комплексных амплитуд. Рассмотрим применение этого метода для расчета индуктивно связанных цепей. Пусть цепь на рисунке 8.1 находится в режиме гармонических колебаний. Запишем уравнения (8.3), (8.4) в комплексной форме:
 ; (8.5)
; (8.5)
 , (8.6)
, (8.6)
где 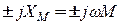 - комплекс сопротивления взаимоиндукции; знак плюс (+ М) ставят при согласном включении катушек; знак минус (- М) - при их встречном включении.
- комплекс сопротивления взаимоиндукции; знак плюс (+ М) ставят при согласном включении катушек; знак минус (- М) - при их встречном включении.