Метод Эйлера решения задачи Коши. Геометрический смысл метода Эйлера

Лекция 34. Численные методы решения задачи Коши (продолжение)

План

Метод Эйлера решения задачи Коши. Геометрический смысл метода Эйлера

Устойчивые и неустойчивые дифференциальные уравнения

Класс вычислительных формул решения задачи Коши, основанных на квадратурных формулах численного интегрирования

Метод Эйлера решения задачи Коши. Геометрический смысл метода Эйлера

Рассмотрим случай использования рассчетной формулы (2) предыдущей лекции, когда . Тогда формула (3) предыдущей лекции примет вид:

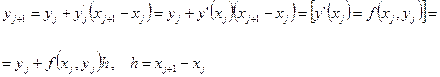(4)

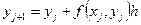
— формула Ейлера.

Геометрический смысл формулы Эйлера представлен на рисунке 1.

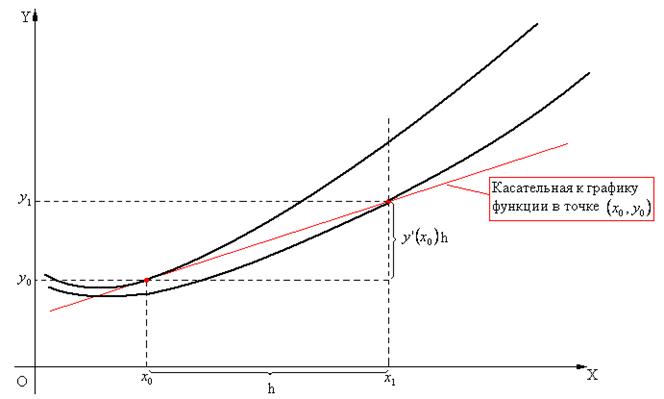
Рис.1.

В общем случае на каждом шаге приближения приближенное решение переходит на новую кривую из представленного множества решений. Для некоторых дифференционных уравнений это вызывает большие погрешности. Например, если мы имеем уравнение 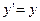, погрешность, которую мы имели на первых шагах приближения, будет сильно возрастать. Такое явление называется неустойчивостью дифференционного уравнения.

Рассмотрим уравнение :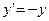

, , , , .

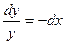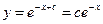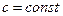Множество решений изображено на рис.2.

Рис.2

Погрешность, которую мы допустили сначала, будет уменьшаться. Такое явление называется устойчивостью дифференционного уравнения.