
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод простой итерации
|
|
Уравнение (2.1) записывают в виде разрешенном, относительно x:
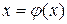 . (1.2)
. (1.2)
Заметим, что переход от записи уравнения (1.1) к эквивалентной записи (1.2) можно сделать многими способами, например, положив
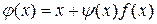 , (1.3)
, (1.3)
где 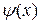 - произвольная, непрерывная, знакопостоянная функция. Часто достаточно выбрать функцию
- произвольная, непрерывная, знакопостоянная функция. Часто достаточно выбрать функцию 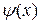 как константу y =const из диапазона ±0.1 - 0.9.
как константу y =const из диапазона ±0.1 - 0.9.
В этом случае корни уравнения (1.2) являются также корнями (1.1), и наоборот.
Исходя из записи (1.2) члены рекуррентной последовательности в методе простой итерации вычисляются по закону
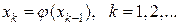 . (1.4)
. (1.4)
Метод является одношаговым, так как последовательность x0, x1, …, xк имеет первый порядок (m=1) и для начала вычислений достаточно знать одно начальное приближение 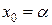 или
или 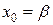 или
или 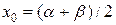 .
.
 Условием сходимости метода простой итерации: если
Условием сходимости метода простой итерации: если 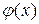 дифференцируема и выполнение неравенства
дифференцируема и выполнение неравенства 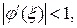 для любого
для любого 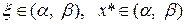 . (1.5)
. (1.5)
Максимальный интервал ( a, b ), для которого выполняется неравенство (1.5), называется областью сходимости.
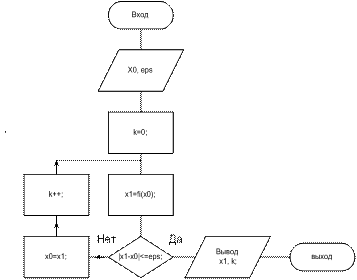
Рис. 1.1.
Схема алгоритма метода простой итерации представлена на рис. 1.1.
В данном алгоритме число проделанных итераций подсчитывает параметр к, а правая часть выражения 1..4 обозначено как «fi». Точность решения – eps. Число итераций лучше ограничить.