
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сложение скоростей
|
|
ЛЕКЦИЯ 3
Сложное движение точки
1. Относительное, переносное и абсолютное движение точки.
2. Сложение скоростей.
3. Сложение ускорений. Теорема Кориолиса.
Относительное, переносное и абсолютное движение точки
Сложным называется движение точки, которое она совершает по отношению к двум системам отсчета, одна из которых неподвижна, а другая движется определенным образом относительно первой.
· Движение, совершаемое точкой M по отношению к подвижным осям координат, называется относительным движением. Траектория AB, описываемая точкой в относительном движении называется относительной траекторией. Скорость движения точки M по отношению к осям Oxyz (то есть вдоль кривой AB) называется относительной скоростью v отн = 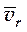 а ускорение точки в этом движении относительным ускорением
а ускорение точки в этом движении относительным ускорением 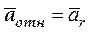 . Из определения следует, что при вычислении vотн и
. Из определения следует, что при вычислении vотн и 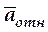 оси Oxyz можно считать неподвижными.
оси Oxyz можно считать неподвижными.
· Движение, совершаемое подвижной системой отсчета Oxyz и всеми неизменно связанными с ней точками пространства по отношению к неподвижной системе O1x1y1z1 является для точки M переносным движением. Скорость той, неизменно связанной с подвижными осями Оxyz точки m, с которой в данный момент совпадает движущаяся точка M, называется переносной скоростью точки M в этот момент (обозначается v пер = 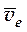 ), а ускорение этой точки — переносным ускорением точки M
), а ускорение этой точки — переносным ускорением точки M 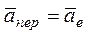 . Таким образом,
. Таким образом, 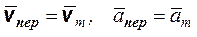 где m — неподвижная по отношению к осям Oxyz точка, с которой в донный момент совпадает точка M.
где m — неподвижная по отношению к осям Oxyz точка, с которой в донный момент совпадает точка M.
· Движение, совершаемое точкой по отношению к неподвижной системе отсчета O1x1y1z 1, называется абсолютным или сложным. Траектория этого движения CD называется абсолютной траекторией, скорость — абсолютной скоростью v a, а ускорение — абсолютным ускорением 
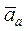
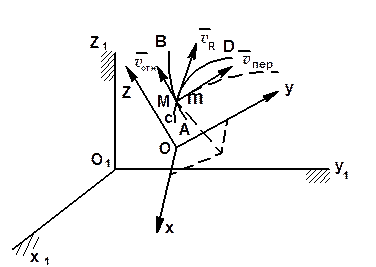
Сложение скоростей
Теорема: при сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей.
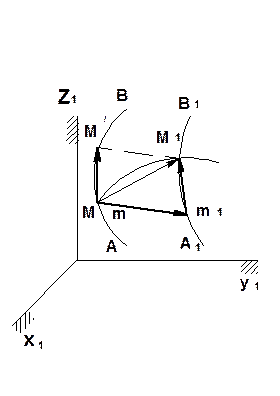
ММ’ - относительное перемещение:
mm1=Mm1 - переносное перемещение:
MM1. - абсолютное перемещение.
|
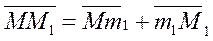
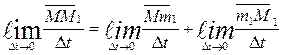
|
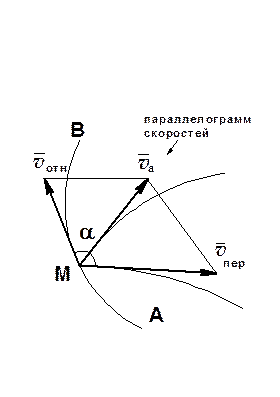
| 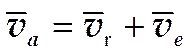
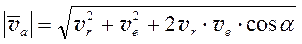 (3.2)
или
(3.2)
или
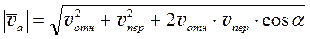
|
С помощью параллелограмма скоростей решается ряд задач кинематики точки, а именно:
– а) зная скорости 
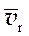 и
и 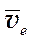 можно найти абсолютную скорость точки
можно найти абсолютную скорость точки 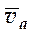 ;
;
– б) зная 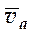 и направление скоростей
и направление скоростей 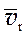 и
и 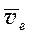 , можно найти модули этих скоростей;
, можно найти модули этих скоростей;
– в) зная скорости 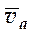 и
и 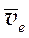 можно найти
можно найти 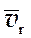 .
.
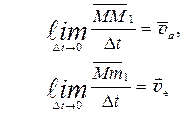
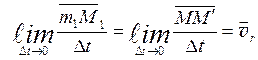
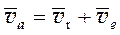 (3.1)
(3.1)