Методы интегрирования д.у. первого порядка

ПРИМЕР ВЫПОЛНЕНИЯ ТИПОВОГО ЗАДАНИЯ

Дифференциальные уравнения первого порядка. Основные понятия и определения.

Обыкновенное дифференциальное уравнение (дифференциальное уравнение, д.у.) относительно функции 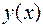- это уравнение, содержащее производные неизвестной функции 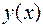. Порядок старшей производной, входящей в уравнение, называется порядком д.у. В общем виде д.у. первого порядка записывается так:

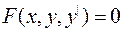(1.1)

Если уравнение (1.1) можно разрешить относительно производной 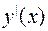, то получим д.у. первого порядка, разрешенное относительно производной

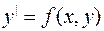(1.2)

Представив производную как отношение дифференциалов: 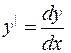, д.у. (1.2) можно записать в дифференциальной форме

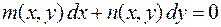(1.3)

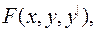
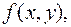
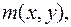
Здесь функции 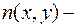известные функции указанных аргументов.

В инженерной практике большое применение имеет задача Коши: найти решение д.у. (1.2), удовлетворяющее начальным условиям:

при 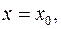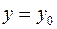(1.4)

Теорема Пикара (достаточное условие существования и единственности решения задачи Коши): если в окрестности точки 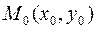функция 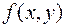непрерывна и ее частная производная 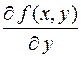ограничена, то решение задачи Коши (1.2), (1.4) существует и единственно.

Общим решением д.у. 1-го порядка называется однопараметрическое семейство его решений:

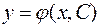(1.5)

где функция 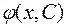такая, что решение задачи Коши (1.2), (1.4) для тех точек 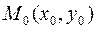, где оно существует и единственно, может быть получено из формулы (1.5) выбором произвольной постоянной С. Частным решением называется решение (1.5) при фиксированной постоянной С. Особым решением д.у. называется такое его решение, которое из (1.5) не может быть получено выбором постоянной С. Нахождение решений д.у. называется интегрированием д.у. Решение д.у. в неявной форме называется интегралом д.у. (частным, общим или особым).

Методы интегрирования д.у. первого порядка

2. 1. Уравнения простейшего типа: 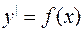. Общее решение имеет вид:

(2.1)

2. 2. Уравнения с разделенными переменными:

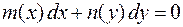(2.2)

Общий интеграл уравнения (2.2) имеет вид

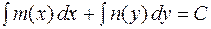(2.3)

2. 3. Уравнения с разделяющимися переменными (УРП):

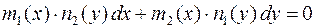(или 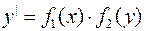) ( 2.4 )

Разделив обе части уравнения на (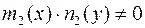), придем к уравнению с разделенными переменными. Общий интеграл уравнения (2.4):

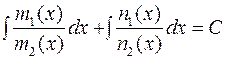(2.5)

2. 4. Однородные уравнения: 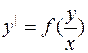или

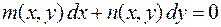, (2.6)

где 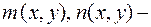однородные функции одного порядка 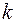, т.е.

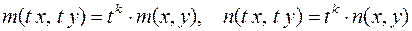
Заменой или 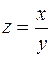однородное уравнение сводится к уравнению с разделяющимися переменными (2. 4).

2. 5. Линейное уравнение первого порядка:

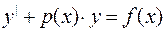(2.7)

Решение уравнения можно найти методом Бернулли и методом Лагранжа. Согласно методу Бернулли решение ищется в виде произведения двух функций: 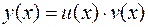, что приводит к системе простых уравнений:

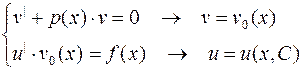
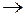
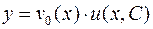- (2.8)

общее решение уравнения (2.7).

2. 6. Уравнение Бернулли: ,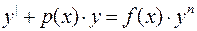

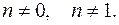
Метод Бернулли: 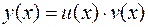приводит к системе уравнений

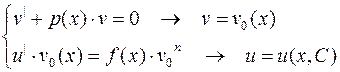
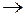
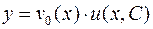- (2.9)

общее решение уравнения Бернулли.

2. 7. Уравнения в полных дифференциалах.

Для того чтобы уравнение

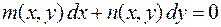(2.10)

было уравнением в полных дифференциалах, необходимо и достаточно, чтобы функции 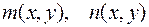были непрерывными в некоторой области 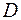, и чтобы выполнялось условие в области :

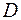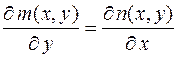(2.11)

Тогда общий интеграл уравнения (2.10) имеет вид:

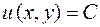, (2.12)

где потенциал определяется из системы уравнений

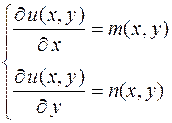
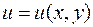(2.13)

Для определения можно пользоваться готовой формулой [1]:

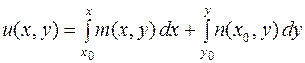, (2.14)

где 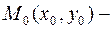любая точка из области .

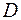Д.у. второго порядка. Основные понятия и определения

В этом пункте в основном повторяются положения п. 1. Д.у. 2-го порядка в общем виде записывается так:

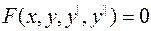(3.1)

Если уравнение (3.1) можно разрешить относительно 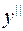, то получим д.у. 2-го порядка, разрешенное относительно старшей производной

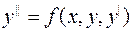(3.2)

Формулировка задачи Коши: найти решение уравнения (3.2), удовлетворяющее начальным условиям:

при 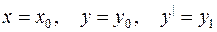(3.3)

где 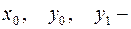известные числа.

Достаточные условия существования и единственности решения задачи Коши: если в окрестности точки 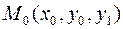функция 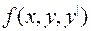непрерывна и ее частные производные 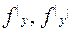ограничены, то решение задачи Коши (3.2), (3.3) существует и единственно.