Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
I. Понятие окрестности
|
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО
ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ВОДНЫХ КОММУНИКАЦИЙ
————————————————————————————————
Ястребов М.Ю.
МАТЕМАТИКА
َ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Утверждено Редакционно-издательским советом
университета в качестве учебного пособия
Санкт-Петербург
УДК
ББК
Рецензент:
Кандидат физико-математических наук, доцент
Кузнецов В.О.
Ястребов М.Ю. Математика. Функции нескольких переменных. — Учебное пособие: СПб: СПГУВК, 2006 — 48 С.
Учебное пособие предназначено для студентов первого курса экономических и технических специальностей. Оно соответствует рабочей программе дисциплины «Математика» и может быть использовано как при подготовке к экзамену, так и для текущих учебных занятий.
УДК
ББК
© Санкт-Петербургский государственный
Университет водных коммуникаций, 2006
Понятие функции нескольких переменных
I. Понятие окрестности
 |
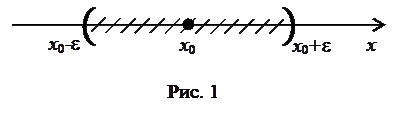На числовой оси
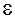- окрестностью точки 
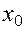называется совокупность 
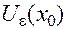точек 
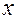, удаленных от 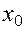меньше чем на : 
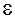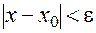. Эта окрестность является интервалом 
(рис. 1).
Также и на плоскости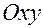 
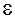- окрестностью точки 
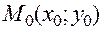называется совокупность 
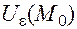точек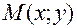 
, удаленных от 
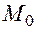меньше чем на :
.
 |
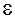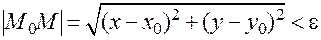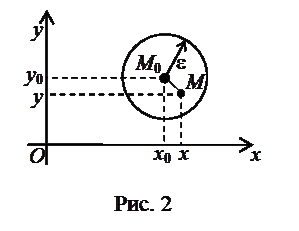Эта окрестность является открытым кругом (без граничной окружности, так как неравенство строгое) радиуса
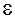с центром в точке 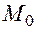(рис. 2).
Аналогично в пространстве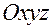 
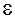- окрестностью точки 
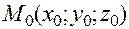называется совокупность 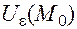точек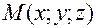 
, для которых
.
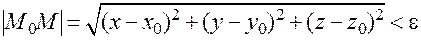Эта окрестность является открытым шаром (без граничной сферы) радиуса 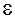с центром в точке 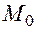(рис. 3).
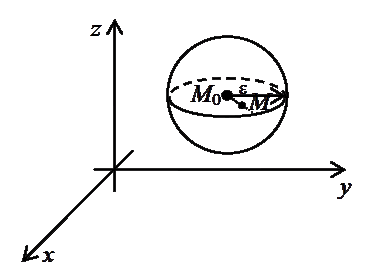
Рис. 3
Рис. 3