
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Залежність між вартістю основних виробничих засобів, реалізованою продукцією та середньообліковою кількістю працівників
|
|
| Групи заводів за вартістю основних виробничих засобів, млн. грн. | Число заводів | Середньорічна вартість основних виробничих засобів, млн. грн. | Реалізована продукція, млн. грн. | Середньооблікова кількість працівників, осіб. | |||
| разом | в середньому | разом | в середньому | разом | в середньому | ||
| 28, 60 – 44, 40 | 163, 3 | 33, 3 | 360, 2 | 72, 0 | |||
| 44, 41 – 60, 20 | 262, 3 | 52, 5 | 484, 5 | 96, 9 | |||
| 60, 21 – 76, 00 | 139, 7 | 69, 9 | 224, 4 | 112, 2 | |||
| 76, 01 – 91, 80 | 251, 9 | 84, 0 | 473, 4 | 157, 8 | |||
| По сукупності | 820, 2 | 54, 7 | 1542, 5 | 102, 8 |
Проаналізувавши середні значення показників у групах, можна зробити висновок про те, що із збільшенням вартості основних виробничих засобів зростає реалізована продукція, проте з середньообліковою кількістю працівників чіткої залежності немає.
Завдання 2. Тема «Узагальнюючі статистичні показники»
Абсолютні величини характеризують кількість одиниць у сукупності, а також розмір, обсяг або рівень ознак. Вони поділяються на індивідуальні, групові та загальні. Останні мають назву «обсяг ознаки» і визначаються по сукупності загалом. Абсолютні величини – це завжди іменовані числа. Використовують натуральні, трудові та вартісні (грошові) одиниці їх виміру.
Відносні величини характеризують співвідношення між ознаками, тобто це є результат порівняння двох показників, який одержують шляхом ділення. Отже, 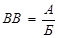 , де А – порівнюваний показник; В – база порівняння.
, де А – порівнюваний показник; В – база порівняння.
Відносні величини показують: а) у скільки разів один показник більший (менший) у порівнянні з іншим; б) яку частку одна величина становить від іншої; в) скільки одиниць однієї величини припадає на одиницю (10, 100, 1000) іншої.
Форми виразу відносної величини:
коефіцієнт: 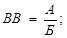 процент:
процент: 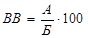 ; проміле:
; проміле: 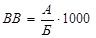 та ін.
та ін.
Залежно від економічного змісту та методики обчислення розрізняють такі види відносних величин: планового завдання, виконання плану, динаміки, структури, координації, порівняння, інтенсивності.
Завдання 2 п. 1 передбачає розрахунок відносних величин планового завдання (ВВпз), виконання плану (ВВвп) і динаміки (ВВд) за реалізованою продукцією. Ці відносні величини розраховують (переважно у процентах) за формулами:
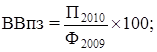
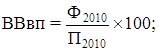
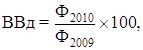 (2)
(2)
де Ф2009, Ф2010, П2010 – фактична та планова реалізована продукція у відповідному році.
Для виконання розрахунків доцільно сформувати таблицю з відповідними показниками для перших 5-ти заводів (графи 5, 6, 7 вихідної таблиці), виконати розрахунки за формулами (2) та внести результати у графи таблиці (рис. 13).
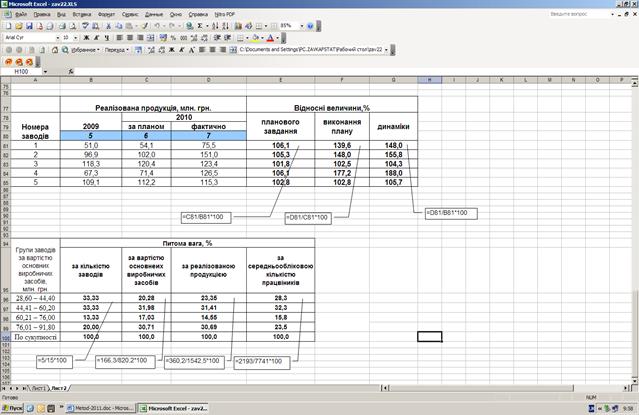
Рис. 13. Розрахунок відносних величин планового завдання,
виконання плану та динаміки
Отже, за результатами розрахунків можна зробити, наприклад, такі висновки: по заводу №1 у 2010 р. у порівнянні з 2009 р. планувалося збільшити реалізовану продукцію на 6, 1%, план перевиконано на 36, 6%, а фактично її зростання становило 48, 0%. Аналогічні висновки можна сформулювати й для інших заводів.
Завдання 2 п. 2 передбачає визначення відносної величини структури (питомої ваги) за формулою:
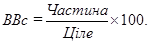
Питома вага кожної групи розраховується за результатами аналітичного групування (завдання 1, табл.1). Для розрахунків відносних величин у відповідні комірки таблиці введемо формули (див. рис. 13), а результати розрахунків розташуємо у відповідних клітинках таблиці. З одержаних значень видно, що у першу групу увійшло 33, 3% заводів, на неї припадає 20, 3% основних виробничих засобів, 23, 4% реалізованої продукції та 28, 3% кількості працівників. Аналогічні висновки необхідно зробити й по інших групах.
Завдання 2 п. 3 передбачає розрахунок відносних величин інтенсивності та порівняння. Відносну величину інтенсивності (ВВінт) визначають як відношення двох різних показників і переважно характеризує ступінь поширення чи розвитку явища у певному середовищі:
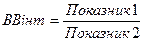 . (3)
. (3)
Ця відносна величина може мати одиниці виміру вихідних показників, а форма її виразу визначається сутністю досліджуваних процесів та економічною логікою.
Відносна величина порівняння (ВВп) – це співвідношення однойменних показників, які обчислені по різних об’єктах або територіях за однаковий час:
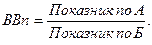 (4)
(4)
Для розрахунку відносних величин інтенсивності за середньорічною вартістю основних виробничих засобів, реалізованою продукцією та середньообліковою кількістю працівників для перших 5-ти заводів доцільно сформувати таблицю з даними, використовуючи графи 1, 2, 5, 7, 8, 9 вихідної таблиці (рис. 14), а потім виконати розрахунки за формулами (3) і (4).
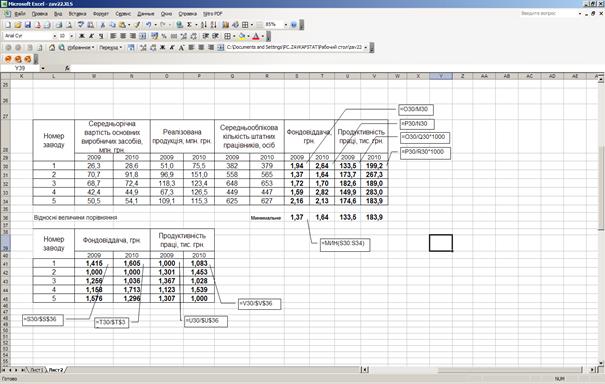
Рис. 14. Розрахунок відносних величин інтенсивності та порівняння
Середня величина – це узагальнюючий показник однорідної сукупності, який характеризує типовий рівень ознаки у розрахунку на одиницю сукупності. Застосовують декілька видів середніх: середня арифметична проста і зважена, середня гармонійна проста і зважена, середня геометрична, мода, медіана та інші.
Найбільш поширеним видом середньої величини є середня арифметична, загальна логічна формула якої має вигляд:
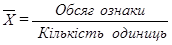 .
.
За наявності індивідуальних даних використовують середню арифметичну просту:
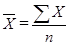 ,
,
де X – значення осереднюваної ознаки.
Якщо наявний дискретний або інтервальний ряд розподілу, використовують середню арифметичну зважену:
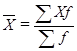 ,
,
де Х – варіанти; f – частоти.
Завдання 2 п. 4 передбачає, що середню фактичну ціну та собівартість продукції А слід розраховувати як середню арифметичну зважену, оскільки вихідні дані є дискретним рядом розподілу, за формулами:
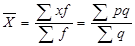 ,
, 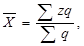 (5)
(5)
де р, z – відповідно ціна та собівартість одиниці продукції; q – кількість вироблених одиниць.
Для обчислення середніх величин за формулами (5) доцільно сформувати масив даних, використовуючи графи 16-21 вихідної таблиці, а для виконання розрахунків у відповідні комірки внеси формули (рис. 15).
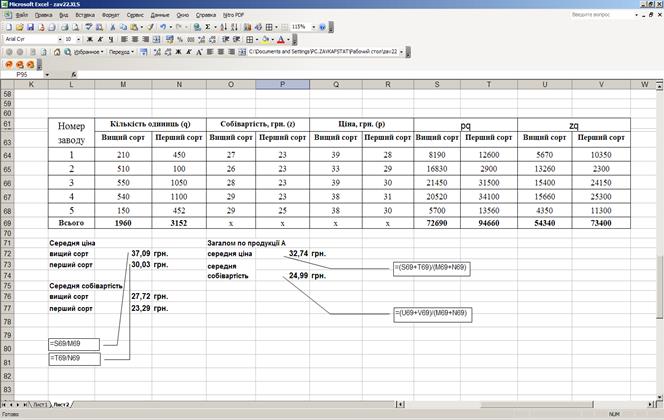
Рис. 15. Розрахунок середньої ціни та собівартості
Для характеристики розміру варіації ознаки використовують абсолютні показники:
– розмах варіації (R): 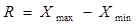 ;
;
– середнє лінійне відхилення (L): просте 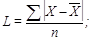 зважене
зважене 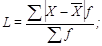
– дисперсію (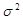 ): просту:
): просту: 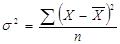 ; зважену:
; зважену: 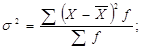
– середнє квадратичне відхилення (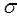 ):
): 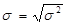 .
.
Слід мати на увазі, що прості показники варіації визначаються за індивідуальними даними, а зважені – у рядах розподілу.
Для порівняння варіації різних показників або одного показника у різних сукупностях застосовують відносні показники варіації:
· коефіцієнт осціляції (Кр): 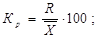

· лінійний коефіцієнт варіації (Кл): 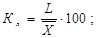
· квадратичний коефіцієнт варіації (V): 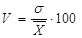 .
.
Останній коефіцієнт використовують найчастіше як для порівнянь, так і для оцінки ступеня (сили) варіації та однорідності сукупності. Вважається, що при V< 33% сукупність є однорідною.
Завдання 2 п. 5 передбачає розрахунок показників варіації фактичної ціни продукції А вищого та першого сортів. Для полегшення обчислень доцільно виконати робочу таблицю з вихідними даними та розрахунковими величинами, використовуючи графи 16, 17.20, 21 вихідної таблиці, потім виконувати розрахунки за відповідними формулами (рис. 16).
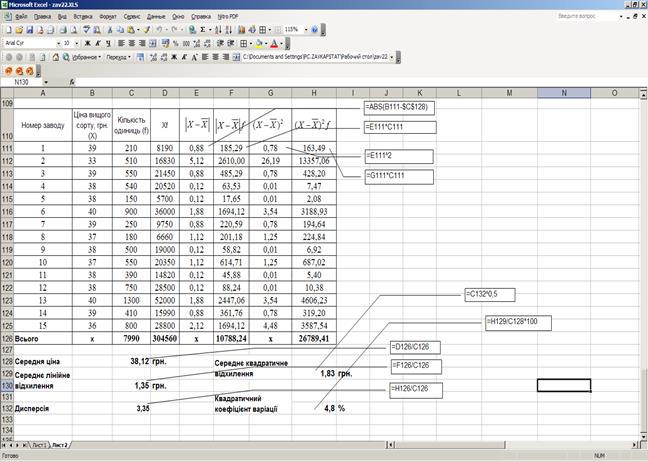
Рис. 16. Розрахунок показників варіації фактичної ціни продукції А
Отже, середня фактична ціна продукції А вищого сорту для 15 заводів становить 38, 12 грн., середній розмір коливань – 1, 83 грн. або 4, 8%. Варіація ціни слабка, а сукупність – однорідна. Аналогічно наведеному прикладу необхідно виконати розрахунки для оцінювання варіації ціни продукції А першого сорту. Порівнявши значення квадратичного коефіцієнта варіації, можна зробити висновки про те, ціна якого виду продукції варіює сильніше.
Завдання 3. Тема «Статистичні методи вимірювання взаємозв'язків»
За статистичною природою взаємозв'язки між показниками поділяють на функціональні та стохастичні (кореляційні). Залежно від напрямку зміни факторного (Х) та результативного (Y) показників розрізняють прямі та обернені зв'язки. За аналітичним виразом взаємозв'язки поділяються на лінійні та нелінійні (параболічні, гіперболічні тощо). Відповідно до сили впливу X на Y виділяють слабкі, середні, сильні (тісні) та дуже сильні взаємозв'язки.
Завдання 3 п. 1 передбачає використання методу аналітичного групування, перший етап якого виконано у завданні 1. Для оцінки тісноти взаємозв'язку між факторним показником (Х) та результативним показником (Y) використовують емпіричне кореляційне відношення (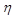 ):
):
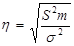 , (6)
, (6)
де S2m – міжгрупова дисперсія результативного показника; 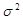 – загальна дисперсія цього показника.
– загальна дисперсія цього показника.
Значення 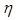 знаходяться в межах від 0 до 1. Чим ближчими є вони до 1, тим сильніший (тісніший) взаємозв'язок між Х та Y.
знаходяться в межах від 0 до 1. Чим ближчими є вони до 1, тим сильніший (тісніший) взаємозв'язок між Х та Y.
Міжгрупову дисперсію(S2m) визначають за результатами аналітичного групування за формулою:
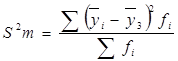 , (7)
, (7)
д е 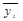 – середнє значення результативного показника у групі;
– середнє значення результативного показника у групі; 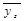 – загальне середнє значення; fi – кількість одиниць у групі.
– загальне середнє значення; fi – кількість одиниць у групі.
Загальну дисперсію результативного показника(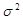 ) можна визначити за формулою:
) можна визначити за формулою:
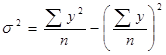 , (8)
, (8)
де у – індивідуальні значення результативного показника.
Тісноту взаємозв'язку між Х та Y характеризує також коефіцієнт детермінації D, який показує, на скільки процентів варіація Y обумовлена варіацією Х: 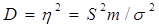 .
.
З метою розрахунку міжгрупової дисперсії для показника «реалізована продукція» за формулою (7) використаємо результати аналітичного групування (завдання 1), які наведено у табл. 2.
Таблиця 2