
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В примерах и задачах;
|
|
План практических занятий
по курсу «Аналитическая геометрия и линейная алгебра»
Й семестр
Часа, 2 контрольные работы, коллоквиум, экзамен
Уч. год
Учебные пособия:
[1] Н.Г. Абрашина-Жадаева и др. Аналитическая геометрия
в примерах и задачах;
[2] А.А. Бурдун и др. Сборник задач по алгебре и аналитической геометрии;
[3] Л.Л. Березкина. Аналитическая геометрия и линейная алгебра
К первому занятию прочитать §§ 1.1 – 1.2, 1.6.
1. Векторы и линейные операции над ними. А: [1]: 1.1;
[2]: 389: В четырехугольнике 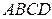 точки
точки 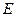 и
и 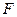 – середины диагоналей
– середины диагоналей 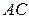 и
и  соответственно. Найдите разложение вектора
соответственно. Найдите разложение вектора  по векторам
по векторам 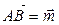 ,
, 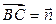 и
и 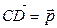 .
.
[1]: 1.8; 1.18 (найти какой-либо вектор, задающий направление биссектрисы внутреннего угла при вершине 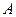 ); 1.22; 1.41; 1.34; (использовать операцию откладывания вектора от точки), 1.4.
); 1.22; 1.41; 1.34; (использовать операцию откладывания вектора от точки), 1.4.
Д: [1]: Контрольные вопросыстр. 7; 1.2; 1.19; 1.20; 1.26.
[2]: 366:  – треугольная пирамида. Докажите, что
– треугольная пирамида. Докажите, что 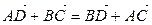 . Верно ли это утверждение для произвольных четырех точек?
. Верно ли это утверждение для произвольных четырех точек?
[3] Прочитать §§ 1.1 – 1.7, примеры 1.1 – 1.10.
2. Скалярное произведение. А: [1]: 1.46; 1.48 ( ); 1.53; 1.63; 1.60.
); 1.53; 1.63; 1.60.
Определить направляющие косинусы ненулевого вектора как косинусы углов, которые этот вектор образует с базисными векторами 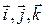 ;
;
[1]: 1.57; 1.59; 1.66 (в).
Д: [1]: Контрольные вопросыстр. 18; 1.42; 1.45; 1.50; 1.56; 1.52*; 1.62, 1.58; 1.21* (неверное условие, см. [3] пример 1.16).
[3] Прочитать §§ 1.7 – 1.9, примеры 1.11 – 1.17. Контрольные вопросы №1.
3. Векторное, смешанное и двойное векторное произведения. А: Тест № 1.
[2]: 466: Вычислите площадь параллелограмма, построенного на векторах 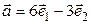 и
и  , если
, если 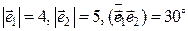 .
.
472: Убедитесь, что векторы 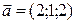 и
и  , отложенные от одной точки, могут служить ребрами куба, и найдите вектор третьего ребра.
, отложенные от одной точки, могут служить ребрами куба, и найдите вектор третьего ребра.
[1]: 1.83; 1.87.
[3] Пример 1.22.Ассоциативно ли векторное произведение, т.е., можно ли утверждать, что для любых векторов 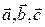 справедливо равенство
справедливо равенство  ?
?
[1]: 1.93 (в).
Д: [1]: Контрольные вопросыстр. 27; 1.68; 1.76; 1.78, 1.85(б), 1.96, 1.32, 1.97.
[3] Прочитать §§ 2.1, 2.4, 2.5; примеры 1.18 – 1.21. 1.23, 1.24. Контрольные вопросы № 2.
4. Прямая на плоскости. А: Тест № 2.
[1]: 2.38 (условие:  – не начальная точка); 2.39, 2.15 (а, б, г); 2.42; 2.48.
– не начальная точка); 2.39, 2.15 (а, б, г); 2.42; 2.48.
() Заданы вершины треугольника 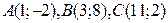 . Составьте:
. Составьте:
а) параметрические уравнения стороны  ;
;
б) канонические уравнения средней линии, параллельной  ;
;
в) общее уравнение высоты, проведенной из вершины  ;
;
г) уравнение медианы, проведенной из вершины  , с угловым коэффициентом.
, с угловым коэффициентом.
() Заданы две прямые на плоскости своими уравнениями: 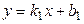 и
и 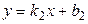 . Вывести формулу для вычисления тангенса угла между этими прямыми (
. Вывести формулу для вычисления тангенса угла между этими прямыми ( ).
).
[2] 590: Составьте уравнение катетов равнобедренного прямоугольного треугольника, зная уравнение его гипотенузы 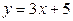 и координаты одной из вершин
и координаты одной из вершин 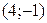 .
.
Д (к занятию 6): 2.6; 2.43; 2.58*; 2.62.
[2] 591: Зная уравнения боковых сторон равнобедренного треугольника  и
и  , составьте уравнение его третьей стороны, при условии, что она проходит через точку
, составьте уравнение его третьей стороны, при условии, что она проходит через точку 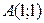 .
.
[3] Прочитать §§ 2.2, 2.3, 2.5, 2.6; примеры 2.9, 2.12*. Контрольные вопросы № 3.
5. Плоскость и прямая в пространстве. А: Тест № 3.
[2] 627: Каковы особенности расположения плоскости 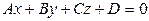 относительно прямоугольной декартовой системы координат, если:
относительно прямоугольной декартовой системы координат, если:
а) 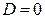 , б)
, б) 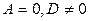 ; в)
; в) 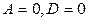 ; г)
; г) 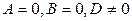 ;
;
д) 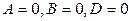 ; е)
; е) 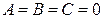 ?
?
[1]: 2.74.
[2] 637: Составьте уравнение плоскости проведенной, через точку 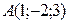 параллельно плоскости, проходящей через точки
параллельно плоскости, проходящей через точки  ,
, 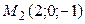 ,
, 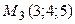 .
.
[1]: 2.100; 2.102 (канонические уравнения), 2.103 (в виде пересечения плоскостей), 2.131.
[2] 691: Составьте общее уравнение плоскости, проходящей через параллельные прямые 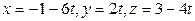 и
и  ;
;
Д: [1]: 2.75(1); 2.70.
[2] 633: Даны вершины треугольной пирамиды 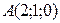 ,
, 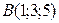 ,
, 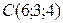 ,
,  . Составьте общее уравнение плоскости, проходящей через ребро
. Составьте общее уравнение плоскости, проходящей через ребро  и середину ребра
и середину ребра 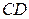 .
.
[1]: 2.71; 2.101; 2.122, 2.125.
[3] Прочитать §§ 2.6, 2.8, 2.9; примеры 2.3 – 2.8, 2.10, 2.11, 2.12*, 2.13*. Контрольные вопросы №4.
6. Плоскость и прямая в пространстве. А: Тест № 4.
[2] 669: Выясните взаимное расположение плоскости  и прямой
и прямой 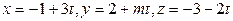 в зависимости от параметра
в зависимости от параметра  .
.
[1]: 2.134 (уравнение прямой 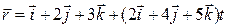 , решение в векторном виде); 2.135 (уравнение плоскости
, решение в векторном виде); 2.135 (уравнение плоскости 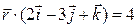 , решение в векторном виде); 2.136(1).
, решение в векторном виде); 2.136(1).
Взаимное расположение прямых в пространстве. Условие всех задач: выясните взаимное расположение прямых в пространстве. В случае пересечения найдите точку пересечения.
[2]: 665 (1) 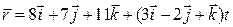 и
и 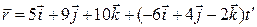 ;
;
665 (3) 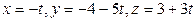 и
и 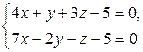 ;
;
666 (1) 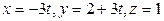 и
и 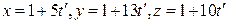 .
.
() Найдите расстояние от точки 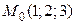 до прямой
до прямой 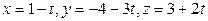 .
.
[1]: 2.82.
[2]: 650: Напишите уравнения плоскостей, делящих пополам двугранные углы, образованные плоскостями 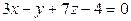 и
и 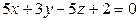 .
.
602: Составьте уравнение биссектрисы угла между прямыми (на плоскости) 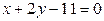 и
и 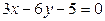 , смежного с тем, которому принадлежит точка
, смежного с тем, которому принадлежит точка 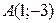 .
.
Д: Выясните взаимное расположение прямых в пространстве. В случае пересечения найдите точку пересечения: [2]: 664 (1) 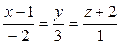 и
и 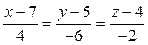 ; 667 (2):
; 667 (2): 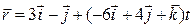 и
и  .
.
689: Составьте общее уравнение плоскости, проходящей через пересекающиеся прямые  и
и  .
.
670 Выясните взаимное расположение плоскости  и прямой
и прямой  в зависимости от значений параметров
в зависимости от значений параметров 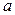 и
и 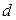 .
.
[1]: 2.111(3); 2.112(2); 2.128*; 2.140; 2.141, 2.33.
[2]: 652: Напишите уравнения плоскостей, параллельных плоскости 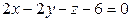 и отстоящих от нее на расстояние, равное 7.
и отстоящих от нее на расстояние, равное 7.
601 (1): Составьте уравнение множества точек, каждая из которых равноудалена от двух параллельных прямых (на плоскости) 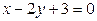 и
и  .
.
[3] Примеры 2.14, 2.15*, 2.16*, 2.17– 2.23.
7. Контрольная работа №1 по разделам: Элементы векторной алгебры. Прямая и плоскость.
Д: [3] Прочитать §§ 3.1 – 3.8. Контрольные вопросы № 5.
8. Линии второго порядка. А: Тест № 5.
[1] 3.4(2), 3.6(3), 3.9(2), 3.18; 3.21*, 3.32(3), 3.41(2), 3.42, 3.51(3), 3.54(4, 7).
Д: [1] 3.3(3), 3.5(3), 3.13(2), 3.30(4), 3.51(4).
[3] Прочитать §§ 4.1 – 4.8. Примеры 3.1. – 3.6.