Матричная форма МНК при построении модели (этап оценки коэффициентов модели).

МНК имеет три этапа:
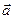= (a0...ak)¢ - вектор- столбец
x = (x1...xk)¢ - вектор- столбец
f(x) = (1, x1,.., xk)¢
- наблюдаемые значения, – оценки, - истинные значения

Эксперимент проводится в N точках, т.о. фиксируем x и y. x1, x2,..., xN - точки экспериментов.
xi= (xi1, xi2,..., xin)¢ 1 £ i £ N
- вектор наблюдений функции отклика.

Для оценки адекватности модели в любой точке xi эксперимент повторяется n раз.

Информационная матрица

- ошибка, погрешность.

Требуемые условия.
1. Результаты наблюдений свободны от систематических ошибок

E - математическое ожидание.
2. Результат наблюдений в точке xj не зависит от результата наблюдений в точке xi.

3. Дисперсия результатов наблюдений во всех точках одинакова.
для любых i.
4. Оценка является несмещенной

5. Дисперсия оценки должна быть минимальна

где - оценка, которая еще пока не найдена.

Так как ¶S/¶a = 0 то следовательно

xi

14. Корреляционное отношение
Применение коэф. корреляции ограничивается случаем линейной связи. Для оценки нелинейной связи используют корреляционное отношение. Корреляционное отношение требует расчета условных дисперсий.
Зависимость Dу׀ х = φ (х) – скедастическая функция. Если φ (х)=const, то условная дисперсия переменной У –постоянна, не зависит от х и говорят, что связь между случайными переменными у и х гомоскедастическая.
Чтобы получить представление о рассеянии случайной переменной у во всем диапазоне изменения переменной Х1используют вероятностную, называемую средней условной дисперсией . По гомоскедастической связи, когда Dу׀ х =const, то ничем не отличается от Dу׀ х. По определению

Установим соотношение между полной дисперсией Dyи средней условной дисперсией . Формула полной дисперсии случайной переменной у записывается в виде
Dy= M[ y2]-m2y, my= M[y]
Cделаем искусственное преобразование. Прибавим и отнимем от правой части M[m2ylx], где mylx= M[y l x] -условное мат.ожидание
Dy= M[ y2 ] - M[m2ylx] + M[m2ylx] - m2y
Вспомним, что = M[ y2] - M[ m2ylx]
M[m2ylx] - m2y= D{M[ylx]}
Это следует из D{M[ylx]} = D[mylx] = M[m2ylx] - {M[mylx]}2 = M[m2ylx]-m2y,
т.е. Dy= + D{M[ylx]} Это формула разбиения дисперсий.

Т.е. полная дисперсия является суммой средней условной дисперсии и дисперсии условного математического ожидания. Поясним это.
Если х – входная, а у – выходная переменные, то дисперсия условного мат. ожидания D{M[ylx]} представляет собой ту часть полной дисперсии Dyвыходной переменной у, которая связана с влиянием входной переменной х.
Вторая часть полной дисперсии – средняя условная дисперсия – определяется влиянием совокупности всех остальных переменных, кроме учтенной переменной х.
Так как = Dy– D{M[ylx]}, то ≤ Dy
Равенство имеет место, когда D{M[ylx]} = 0
В качестве меры корреляц. отношения принято η 2yx=1 - / Dy; η yx– корреляц. отношение

Свойства: 1. 0 ≤ η yx≤ 1; 0 ≤ η xy≤ 1. Это свойство следует из формул
η yx=1- /Dy η xy= 1- /Dx

аналогично
η 2yx= D{ M[ylx] } / Dy η 2xy= D{ М[xly] } / Dx
2. Величина η всегда положительна.
3. Равенство η yx= 0 означает, что переменная y не коррелированна с переменной x. Если x и y – независимы, то η yx= 0.
4. Равенство η yx=1 соответствует функциональной связи между y и x.
5. В общем случае η yx≠ η xy, т.е. данная связь несимметрична

6. Если связь между переменными x и y линейна, то η yx= η xy.
7. При линейной регресии η yx= ׀ ryx׀, т.е. корреляционное отношение служит характеристикой и линейной связи.
8. При нелинейной регрессии всегда η yx> ׀ ryx׀, т.е. коэффициент корреляции при нелинейной стохастической связи дает заниженные оценки.
Разность η 2yx-r2yx=h2yx– индикатор степени нелинейности стохастической связи.