
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Собственные колебания систем с n степенями свободы.
|
|
Рассмотрим невесомую раму, несущую n сосредоточенных масс, имеющих по одной степени свободы. Отклоним конструкцию от состояния статического равновесия и предоставим ее самой себе. Каждая из масс начнет совершать сложное движение, складывающееся из n простых движений следующего вида: 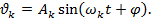
Pni Pnn
mi mn

|

|
m2 Pn, 1
m1
Исследуем это движение.
Применим к движущейся системе принцип Даламбера, который позволяет заменить дифференциальные уравнения движения квазистатическими уравнениями равновесия. Приложим к каждой массе силу инерции 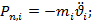
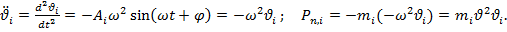
Как видно, сила инерции пропорциональна массе перемещению и квадрату частоты.
Вычислим перемещение по направлению степени свободы i массы, используя принцип суперпозиции:
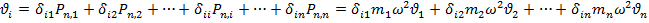
Приведем подробные члены и разделим на квадрат частоты:
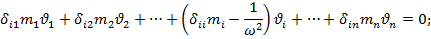
Раскрывая по всем i=1, 2, …, n, получаем систему однородных алгебраических уравнений относительно перемещений.
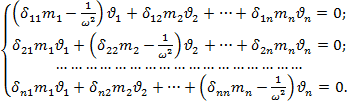 (*)
(*)
Для получения нетривиального решения необходимо потребовать, чтобы определитель, составленный из коэффициентов при неизвестных, обращался в ноль.
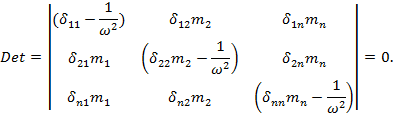
Раскрывая определитель, получаем алгебраическое уравнение n степени относительно величины 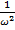 .
.
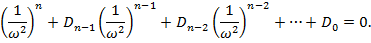
Это уравнение называется уравнением частот, или вековым уравнением. В коэффициенты 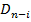 будут входить податливость и массы.
будут входить податливость и массы.
Решая уравнение, находим n действительных корней 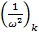 , и, следовательно, n различных частот колебаний
, и, следовательно, n различных частот колебаний 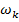 .
.
Сложное движение каждой массы будет складываться из простых движений, соответствующих частотам колебаний.
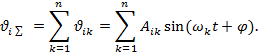
Совокупность простых движений всех масс системы для какой-либо частоты колебаний определяет форму колебаний для этой частоты.
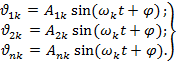 k форма колебаний.
k форма колебаний.
Амплитудной формой колебаний называют такое отклонение системы от состояния равновесия, для которого 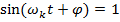 . Каждая масса получает амплитудное перемещение
. Каждая масса получает амплитудное перемещение 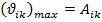 , которое можно найти как результат действия системы максимальных сил инерции.
, которое можно найти как результат действия системы максимальных сил инерции.
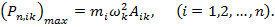
Чтобы определить 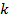 амплитудную форму колебания конструкции, необходимо решить систему однородных уравнений, получаемых из (*).
амплитудную форму колебания конструкции, необходимо решить систему однородных уравнений, получаемых из (*).
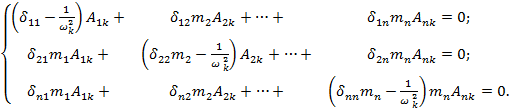 (**)
(**)
Так как определитель равен нулю, то система имеет несчетное множество решений. Обычно ее решают с точностью до постоянного множителя, полагая 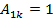 и отбрасывая, как лишнее, последнее уравнение системы, которое используют для проверки.
и отбрасывая, как лишнее, последнее уравнение системы, которое используют для проверки.
Формы колебаний системы обладают свойством ортогональности:
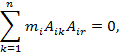
Где 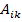 - амплитуда
- амплитуда  массы при
массы при 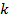 форме колебаний;
форме колебаний;
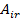 - то же при
- то же при 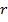 форме колебаний.
форме колебаний.
Если в системах уравнений (*) и (**) удается получить все побочные податливости равными нулю, т.е. 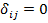 при
при 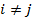 , то системы распадаются на n независимых уравнений и легко решается.
, то системы распадаются на n независимых уравнений и легко решается.
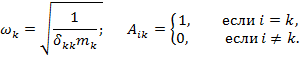
Такие формы колебаний называют главными формами колебаний. В этом случае система с n степенями свободы ведет себя как система с одной степенью свободы, что облегчает динамический расчет.
Рассмотрим два частных случая.