
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Допредельная модель диффузионного процесса
|
|
Рассмотрим реальные процессы, которые достаточно хорошо описываются диффузионными случайными процессами.
Представим себе частицу, совершающую скачкообразные движения по оси X. За время D t частица совершает скачок на величину ±d с вероятностью 1/2, при этом скачки выполняются независимо друг от друга. Через x(T) обозначим координату частицы в момент времени T, через D xk – величину скачка частицы в k -й момент времени. Здесь D xk =±d с вероятностью 1/2. Очевидно, что
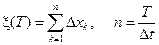 .
.
Найдём среднее значение и дисперсию положения частицы в момент времени T
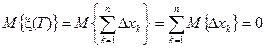 ,
,
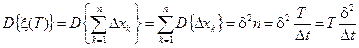 .
.
В пределе, при D t ®0, d®0, возможны три варианта.
а) Если d2=o(Dt), то D{x(T)}®0, а так как M{x(T)}=0, то частица не меняет своего положения, оставаясь в начальной точке. Этот случай не представляет интереса.
б) Если D t = o (d2), то D {x(T)}®¥, следовательно, положение частицы в конечный момент времени T имеет бесконечный разброс, что для реальных процессов невозможно, поэтому такой вариант рассматривать не будем.
в) Если d2= O (D t), то есть эти величины одного порядка малости, например d2= B D t, где B > 0 – некоторая постоянная, тогда D {x(T)}= B. Этот вариант рассмотрим более подробно.
Рассмотрим приращения
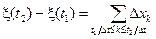 ,
,
для которых можно записать
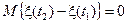 ,
,
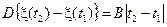 .
.
Тогда в силу центральной предельной теоремы можно записать
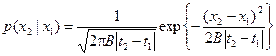 ,
,
и все приращения по предположению независимы. Следовательно, рассматриваемое случайное блуждание в пределе даёт винеровский процесс.
Остановимся на особенностях траекторий винеровского процесса. Так как при D t ®0, величина скачка d®0,, то реализации винеровского процесса непрерывны.
С другой стороны, отношение
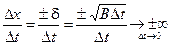 ,
,
то есть производная не существует, поэтому говорят, что реализации винеровского процесса недифференцируемы.
Таким образом, случайное блуждание частица, при достаточно малой величине скачка, можно описать винеровским процессом, то есть диффузионным процессом с коэффициентами переноса, равным нулю, и коэффициентом диффузии, равным некоторой положительной постоянной.
Более общий вариант диффузионного процесса можно получить в пределе, если пролагать, что положительный скачок происходит с вероятностью ½ +a, а отрицательный – с вероятностью ½ –a. Тогда
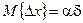 ,
,
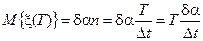 .
.
Так как 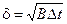 , то
, то
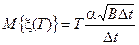 .
.
Полагая, что 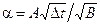 , получим
, получим
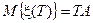 .
.
При этом
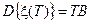 .
.
Нетрудно показать, что при D t ®0 в пределе несимметричное блуждание переходит в диффузионный процесс с коэффициентом переноса – A, и коэффициентом диффузии – B.