Второй учебный вопрос: Дискретная и непрерывная случайная величина, законы их распределения

Случайная величина непосредственно связана со случайными событиями. Появление тех или иных значений случайной величины можно рассматривать как случайные события одного испытания.

Предположим, что производится некоторое испытание, в результате которого может произойти случайное событие. Если пространство элементарных событий этого испытания (или полная группа событий) состоит из событий, которые имеют числовое значение, то это пространство можно рассматривать как множество значений некоторой случайной величины, связанной с данным испытанием.

Так как разные значения случайной величины можно рассматривать как события, а, как известно, случайные события имеют вероятность, то и значения случайной величины имеют также свои вероятности. В этом и проявляется " случайный" характер случайной величины.

Например, случайная величина Х, равная числу очков, выпавших при одном броске игрального кубика, принимает значение равное 1 (выпало одно очко) с вероятностью 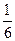, а значение равное 9 (невозможное событие) с вероятностью равной 0.

Таким образом, для полного определения случайной величины необходимо указать какое-либо правило нахождения вероятностей значений этой случайной величины, т.е. задать ее закон распределения.

Законом распределения случайной величины называется любое правило, по которому можно находить вероятности произвольных событий, связанных со случайной величиной.

Это правило может быть задано в виде таблицы, формулы, графика, функции и т.д. Чаще всего, это бывает формула нахождения вероятности того, что случайная величина примет какое-то значение, или, что случайная величина попадет на какой-нибудь интервал.

Существуют стандартные формы задания закона распределения случайной величины, причем эти формы, кроме одной, являются различными для дискретных и непрерывных случайных величин.

Наиболее простые формы закона распределения имеет дискретная случайная величина.