
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Численные методы
|
|
Дано обыкновенное дифференциальное уравнение первого порядка
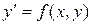 (5.1)
(5.1)
Требуется найти решение у= у(х) этого уравнения, удовлетворяющее начальному условию:
у(х0) = у0 (5.2)
Такая задача называется задачей Коши. Геометрический смысл решения этой задачи состоит в нахождении интегральной кривой у=у(х), проходящей через заданную точку А0 (х0, у0).
 |
Рисунок 5.1. - Интегральная кривая у=у(х),
Численное решение задачи Коши состоит в нахождении значений у1, у2, у3, ….уn в точках 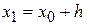 ,
, 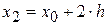 , …,
, …, 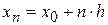 отрезка [a, b], где h - шаг интегрирования, х0 = a, хn = b.
отрезка [a, b], где h - шаг интегрирования, х0 = a, хn = b.
Нанеся точки (х0, у0), (х1, у1), …(хn, уn) на координатную плоскость и соединив их отрезками ломаной прямой, получим ломаную линию, называемую ломаной Эйлера – приближенное изображение интегральной кривой (рис.5.2).


|


|
|


|
|
|
|

Рисунок 5.2 - Ломаная Эйлера.
Метод Эйлера, простейший и сравнительно грубый численный метод интегрирования обыкновенных дифференциальных уравнений, применяется в основном для ориентировочных расчетов.
Метод Эйлера может быть применен к решению систем дифференциальных уравнений.
Пусть задана система двух уравнений первого порядка
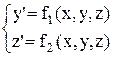
c начальными условиями y(x0)=y0; z(x0)=z0.
Приближенные значения y(xi)≈ yi; z(xi)≈ zi находится по формулам:
yi+1=yi+Δ yi; zi+1=zi+Δ zi,
где Δ yi=hf1(xi, yi, zi); Δ zi=hf2(xi, yi, zi) (i=0, 1, 2, …)
Метод Эйлера обладает малой точностью и дает сравнительно удовлетворительные результаты (в смысле погрешности) лишь при малых значениях h. Так как по существу метод Эйлера заключается в том, что интеграл дифференциального уравнения на каждом частичном отрезке [xi, xi+1] представляется двумя членами ряда Тейлора
y(xi +h)=y(xi)+hy’(xi) (i=0, 1, 2,...),
т.е. для этого отрезка имеется погрешность порядка h2.
Кроме того, при вычислении значений на следующем отрезке исходные данные не являются точными и содержат погрешности, зависящие от неточности предшествующих вычислений. К недостаткам метода следует отнести малую точность и систематическое накопление ошибок.