
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дискретные случайные величины.
|
|
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Определение: Случайной величиной называется величина, которая в результате опыта может принимать определенное (но заранее неизвестное) значение.
Пример: 1) Число студентов на занятии по математике есть дискретная случайная величина 0, 1, 2, …, 25 (если в группе 25 человек), но заранее неизвестно сколько их будет.
2)Скорость встречного автомобиля или ошибка взвешивания на точных весах.
В первом примере случайная величина принимает одно из значений 0, 1, 2, …, 25 - это отдельные изолированные возможные значения.
Во втором примере, случайные величины могут принимать любое значение из промежутка (a, b).нельзя отделить одно возможное значение от другого промежутком.
Значит, целесообразно различить дискретные и непрерывные случайные величины.
Определение: Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, что возможных значений непрерывной случайной величины – бесконечно.
ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.
Случайные величины обозначаются заглавными буквами X, Y, Z.
Запись X=x означает, что случайная величина приняла значение x.
Запись P (X=x) означает вероятность того, что случайная величина X приняла значение x.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Его можно задать таблично, аналитически (в виде формулы) и графически.
Табличный способ (или ряд распределения)
| X | x1 | x2 | x3 | … | xn | - возможные значения |
| P | p1 | p2 | p3 | … | pn | - их вероятности |
Т.к. в одном испытании случайная величина принимает одно и только одно возможное значение, то события X=x1, … X=xn – образуют полную группу, значит,  .
.
Пример: В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и 10 выигрышей по 1руб. Найти закон распределения случайной величины X – стоимости возможного выигрыша для владельца одного билета.
| X | 50 | 1 | 0 |
| P | 
| 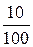
| 1-  - - 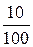
|

Графический ряд распределения (многоугольник или полигон распределения). В прямоугольной системе координат строятся точки  и затем соединяются.
и затем соединяются.