Резонанс напряжений.

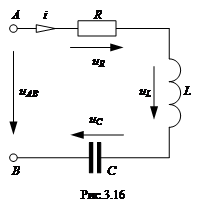Рассмотрим схему с последовательным соединением R, С, L, -элементов (рис. 3.16). Пусть на вход схемы (точки A и B) подается синусоидальное напряжение и_AB = U_m sin(ω t +ψ _u) . Под действием синусоидального напряжения будет протекать синусоидальный ток: i = I_m sin(ω t +ψ _i) .

Связь между этими величинами:

При резонансе напряжений сдвиг фаз φ между током и напряжением, а также реактивное сопротивление x равны нулю:

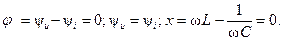
Отсюда следует условие резонанса напряжений:

согласно которому резонанс напряжений может быть получен:

1) изменением частоты: ;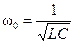

2) изменением индуктивности L катушки: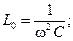

3) изменением емкости С конденсатора: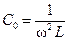

Величина ω ₀ называется резонансной частотой LC -контура, а значения L ₀и С ₀ – резонансными параметрами контура. Поскольку при резонансе Х= 0, то на резонансной частоте полное сопротивление контура носит активный характер:

.

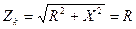Резонансный ток, соответственно, равен: .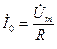

Поскольку φ =0, a cosφ = P / S =1, то при резонансе Р=S.

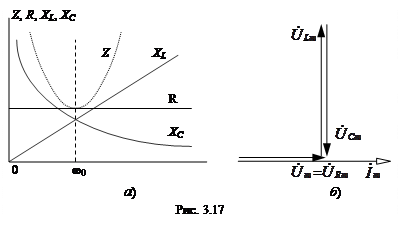
Зависимости сопротивлений R, X_L, X_C, Z от частоты ω представлены на рис. 3.17, а. Эти функции соответствуют уравнениям:

.

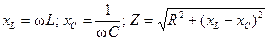Векторная диаграмма тока и напряжений при резонансе показана на рис. 3.17, б. Она соответствует уравнениям:

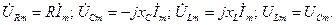
Если сопротивления X_L=X_С больше R, то напряжения на емкости и индуктивности по величине будут превышать входное напряжение.

Количественно это устанавливается при помощи коэффициента, называемого добротностью:

,

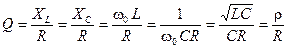где – резонансная частота контура; 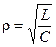– характеристическое сопротивление контура.

Для контуров с сосредоточенными параметрами L, С, R величина добротности Q< 500.

Зависимости I (ω), U_R (ω), U_L (ω), U_C (ω), в схеме рис. 3.16 при изменении частоты ω и неизменной амплитуде U_m входного напряжения называются резонансными кривыми. Они показаны на рис. 3.18, а и б.

Зависимости, показанные на рис. 3.19, а и б, соответствуют уравнениям:

.

Из уравнения 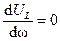определяется частота ω _L, при которой функция U_L (ω) имеет максимум: .

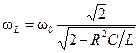Из уравнения находится частота ω _C, при которой функция U_C (ω) имеет максимум: .

Обозначим а =ω /ω ₀. Тогда зависимости I (ω), U_L (ω)можно записать в виде

.

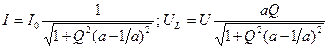На рис. 3.19, б представлены зависимости I / I ₀ от ω /ω ₀ при двух значениях добротности Q ₁ и Q ₂> > Q ₁. Пересечение горизонтальной линии, проведенной на уровне 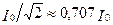(или 0, 5 Р) с резонансными кривыми позволяет определить частоты η ₁ и η ₂.

Разность частот Δ η =η ₁–η ₂ называется относительной полосой пропускания. Разность частот ω ₁=ω ₀η ₁ и и ω ₂=ω ₀η ₂ называется абсолютной полосой пропускания: Δ ω =ω ₁–ω ₂. Можно показать, что ω ₀/Δ ω = Q.

Чем выше добротность, тем уже полоса пропускания. Граничные частоты определяются из уравнения: 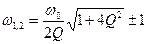. Угол сдвига фаз φ изменяется по закону в пределах от –π /2 до π /2, проходя через 0 при резонансе.