
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Численные методы решения
|
|
Лабораторная работа 1
обыкновенных дифференциальных уравнений (4 часа)
При решении многих физических и геометрических задач приходится искать неизвестную функцию по данному соотношению между неизвестной функцией, ее производными и независимыми переменными. Такое соотношение называется дифференциальным уравнением, а отыскание функции, удовлетворяющей дифференциальному уравнению, называется решением дифференциального уравнения.
Обыкновенным дифференциальным уравнением называется равенство
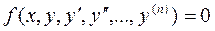 , (1)
, (1)
в котором 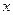 - независимая переменная, изменяющаяся в некотором отрезке
- независимая переменная, изменяющаяся в некотором отрезке 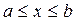 , а
, а  - неизвестная функция y(x) и ее первые n производные.
- неизвестная функция y(x) и ее первые n производные.
Число  называется порядком уравнения.
называется порядком уравнения.
Задача заключается в нахождении функции y, удовлетворяющей равенству (1). Более того, не оговаривая это отдельно, будем предполагать, что искомое решение обладает той или иной степенью гладкости, необходимой для построения и «законного» применения того или иного метода.
Различают два типа обыкновенных дифференциальных уравнений
- уравнения без начальных условий
- уравнения с начальными условиями.
Уравнения без начальных условий - это уравнение вида (1).
Уравнение с начальными условиями - это уравнение вида (1), в котором требуется найти такую функцию 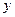 , которая при некотором
, которая при некотором 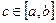 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
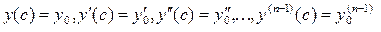 ,
,
т.е. в точке 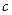 функция
функция 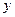 и ее первые
и ее первые  производных принимают наперед заданные значения.
производных принимают наперед заданные значения.