КАТЕГОРИИ:

Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Причинный анализ

⇐ ПредыдущаяСтр 17 из 17

Существо проблемы причинного анализа можно представить следующим образом. Имеет место какое-либо социальное явление, которое характеризуется переменной х. Оно зависит и причинно обусловлено другими данными социальными явлениями, характеризуемыми соответственно переменными y, z и т.д. Требуется определить степень этой зависимости. Быть может, переменные y, z не составляют все влияние на х, и тогда не учтенное в данном наблюдении влияние обозначим х. Переменные х могут сами, в свою очередь, быть связаны между собой. Быть может, что некоторые из переменных слабо связаны или не прямо связаны с х. Необходимо оставить только существенные связи. В социологии проблему такого анализа эмпирических данных впервые начал решать Э. Дюркгейм, следуя миллевской традиции причинного вывода и весьма скрупулезно используя правило сопутствующих изменений из массы статистических данных осамоубийстве.

Между двумя переменными возможны такие структурные отношения:

(х обусловливает у)

(у обусловливает х)

(взаимное воздействие)

(нет связи)

Структурные отношения для трех переменных см. на рис. 17.

Для последних двух случаев может оказаться, что

, а ,

и из эмпирических данных нельзя будет решить, какая здесь структура.

Коэффициент корреляции между х и у не равен нулю () и означает, что между х и у есть связь. Частный коэффициент корреляции между х и у при постоянном z равен нулю и означает, что связь между х и у обусловлена не их собственным воздействием, а действием переменной z (рис. 18).

Для этих случаев () и () частный коэффициент корреляции между х и у при постоянном z равен нулю. Случай () есть так называемая ложная корреляция.

Только анализ причинных связей между переменными может позволить выявить структуру данной эмпирической системы переменных.

В первые десятилетия ХХв. обостряется интерес к проблеме причинности. С одной стороны, он обусловлен развитием квантовой

физики в связи с соотношением динамических и статистических закономерностей и выявлением ограниченности лапласовского детерминизма в рамках действующей силовой причинности. С другой стороны, этот интерес вызван развитием эмпирических неэкспериментальных наук – демографии, эконометрики, социологии. Оно привело красширению представлений о причинности, в какой-то мере – возврату к Аристотелю. В физике, естествознании причинность понималась как действующая причина, силовое взаимодействие. Эконометрика показала существование также иной причины, связанной с нормой, правилом, или «программной обусловленностью»[165].

Эконометрика стала, по словам известного шведского специалиста Г. Уолда[166], пионером в изучении эмпирических неэкспериментальных данных.

Именно с эконометрикой, а затем с социологией наряду с квантовой механикой связано возрождение интереса кпроблеме причинности. Вопрос, касающийся эмпирических данных в неэкспериментальной ситуации, впервые поставил А. Курно в отношении цены, функций спроса и предложений в условиях свободной конкуренции на рынке. Затем это получило развитие в системе уравнений равновесия Вальраса, «закона Парето», гарвардском барометре, большом числе работ по построению функций спроса и производственных функций. В этих экономических исследованиях анализировались эмпирические данные средствами математической статистики. Если при исследовании плодородия почвы или качества удобрений статистические методы применяются

и были выработаны в экспериментальной ситуации, при которой специальным выбором исследуемых участков почвы можно было изолировать действие ряда фактов, чтобы проконтролировать исследуемый фактор, то в эконометрике столкнулись с эмпирической неэкспериментальной ситуацией. Проблема здесь упирается в наличие сложной системы множественных связей, каждая из которых не может быть изолирована и проконтролирована в эксперименте. Чтобы разрубить этот узел, эконометрика обратилась к понятию причинности только не в современном физическом смысле, а скорее, в аристотелевском понимании и ввела понятие причинных моделей[167] (первоначально задача стояла в вы- явлении связей между системой эмпирических данных). Можно написать структурные уравнения между этими переменными и полученную систему решать методом наименьших квадратов. Оказывается, что система структурных уравнений решается, если выделены так называемые экзогенные переменные, т.е. переменные, которые не определяются в данной системе, и так называемые эндогенные переменные, определяемые в данной системе[168].

Эконометрика связана с неэкспериментальным построением моделей. Дуализм экспериментального и неэкспериментального построения уходит в глубь научного метода. Экспериментальные модели предиктивны. Неэкспериментальный метод, развитый в эконометрике, сталкивается с множеством проблем на всех уровнях, от уровня самых общих оснований научного метода до специальных технических проблем. Мы остановимся на двух ключевых проблемах. Первая относится к научной эволюции от детерминистских моделей к стохастическим. Статистическая картина иногда вызвана внешними причинами – ошибками наблюдений, иногда внутренними. В обоих случаях важна проблема «выбора регрессии». Проблема стохастических моделей возникла как проблема Макпранга. Проблема Макпранга разрешается, если ввести причинные отношения. Функция спроса есть причинно- следственное отношение с ценой в качестве причины и спросом в качестве следствия. Спрос обусловливается изменением цены и выражается уравнением регрессии спроса на цену. Механизм ценообразования включает и спрос потребителя, и предложение производителя и не является просто обратным отношением функции спроса. В итоге выбор регрессии есть выбор между причинными моделями, а выбор между моделями определяет выбор между регрессиями.

Вторая проблема связана с различием причинных и непричинных моделей предсказания. Неэкспериментальные модели основываются на прошлых наблюдениях, и модель суммирует регулярности, наблюдаемые в прошлом. В прогнозной модели прошлые регулярности сохраняются в будущем. Прогноз в отношении неэкспериментального построения модели есть то же самое, что повторение в контролируемом эксперименте.

Причинные связи между переменными стали изображать графически в виде диаграмм Райта, по имени биолога С. Райта, который в 20-х годах в изучении факторов наследственности применил подобные диаграммы и разработал специальный метод анализа причинных связей[169]. Если можно в какой-то степени понять антикаузализм Рассела в отношении причинности в классической физике, в которой она неотделима от экспериментальной ситуации и действующего закона, то в исследовании системы взаимосвязанных эмпирических переменных неэкспериментальных наук понятие причинности становится необходимым регулятивным и эвристическим принципом.

Для эмпирических данных определяются коэффициенты корреляции всех порядков. Мы говорим, что есть причины , еcлис изменением , изменяется в среднем , при условии, что все остальные переменные постоянны. В этом случае на диаграмме эти две переменные связываются стрелкой от к . Если же нет прямой связи между двумя переменными при условии постоянства всех других переменных, то на диаграмме переменные не связаны стрелкой. В этом случае частный коэффициент корреляции определенного порядка равен нулю (рис. 19).

Априорно определяется возможный порядок воздействия переменных. В данных случаях принимается следующий порядок: воздействует на все переменные, на нее ни одна не воздействует; –на все, кроме ; –на ; не воздействует ни на одну переменную. Этот порядок обусловленности есть условие причинности.

Как только установлены по значению коэффициентов корреляции соответствующие причинные схемы, пишутся структурные уравнения, в рекурсивной форме (или близкой к ней). Их коэффициенты дают меру причинного влияния переменных.

Г. Саймон впервые применил анализ причинных связей, развитый в эконометрике ксоциологической проблематике[170].

Основная идея метода (обычно в социологической литературе он называется методом Саймона – Блэйлока) состоит в том, что хотя причинные отношения невозможно установить на основе данных о корреляциях, однако можно делать определенные выводы о причинных связях, рассматривая ряд альтернативных моделей и исключая те из них, предсказания по которым не согласуются с эмпирическими наблюдениями.

Такие медали включают: а) конечный набор явно определенных переменных, б) гипотезы о причинных взаимосвязях этих переменных и в) допущения о том, что возможное влияние внешних неучтенных переменных не нарушает наблюдаемую картину причинных связей между явными переменными. Метод Саймона- Блэйлока позволяет в ряде случаев предсказывать величины взаимных корреляций, давая тем самым эмпирически критерий оценки адекватности причинной модели.

Например, причинную структуру, изображаемую графом связей на рис. 20, Саймон предлагает описывать следующей системой уравнений (которые в эконометрике называются структурными

уравнениями):

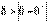
(1)

где , , и –изучаемые признаки, а , и – неявные факторы. При определенных допущениях коэффициенты равны соответствующим частным коэффициентам регрессии (например, ).При отсутствии какой-либо из связей в причинной структуре соответствующий коэффициент будет равен нулю и может служить эмпирическим критерием проверки адекватности модели.

Например, для графа, изображенного на рис. 21, коэффициент и, следовательно, частный коэффициент корреляции поскольку

(2)

то

Таким образом, если гипотетическая причинная структура подтверждается, то уравнение (2) должно удовлетворяться для эмпирических коэффициентов корреляции[171]. Аналогичным образом можно поступать в общем случае, т.е. частный коэффициент корреляции двух признаков, между которыми, по предположению, нет причинной связи, при фиксированных остальных должен быть равен нулю.

Не останавливаясь подробно на этих процедурах, следует сделать ряд общих замечаний относительно метода Саймона – Блэйлока.

Предложенный метод в определенных ситуациях действительно позволяет выделять из ряда альтернативных структур структуру связей, согласующуюся с эмпирическими данными. Тем не менее во многих случаях эти структуры остаются неразличимы. Кроме того, оказывается весьма неудовлетворительной интерпретация коэффициентов структурных уравнений.

В дальнейшем проблема интерпретации коэффициентов была решена Будоном[172],

который показал связь между подходом Саймона – Блэйлока и работами С. Райта[173].

Самым простым подходом к описанию причинных связей между изучаемыми признаками является представление их системой линейных уравнений такого вида:

(3)

...........

где , –переменные, соответствующие исследуемым признакам; 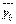, –дополнительные факторы, влияние которых необходимо учесть, но либо неизвестно, что это за факторы, либо неясны направления связей между ними и явными переменными .

Решение этой системы уравнений связано с проблемой идентификации, т.е. встает вопрос, можно ли параметры системы определить из совместного наблюдения над переменными . Эта задача достаточно подробно изучена в математической экономике, и мы коснемся ее лишь в самых общих чертах.

Вся эмпирическая информация о зависимостях между переменными суммируется в таблице эмпирических корреляций. Исходя из этой таблицы и необходимо получить оценки коэффициентов структурных уравнений (3). Нас будут интере- совать условия, при которых могут быть получены оценки по методу наименьших квадратов, т.е. при каких условиях эти уравнения можно рассматривать как регрессионные уравнения.

Основные подходы и проблемы будут ясны при рассмотрении структуры связей простейшего типа.

Здесь –объясняющие переменные (их будем называть независимыми переменными).

–признак, объясняемый непосредственным действием на него других явно выделенных признаков и неявного

фактора, рассматривается как обобщенный неявный фактор.

Предполагается, что могут быть связаны ненаправленной корреляционной связью (это может осуществляться через посредство неявных факторов, действующих на и коррелирующих между собой).

Предполагая, что связи между переменными носят линейный характер, граф связей на рис. 22 эквивалентным образом можно описать линейным уравнением

(4)

Если и не коррелирует с , то для оценки параметров уравнения применим метод наименьших квадратов, и тогда неизвестные параметры будут совпадать с частными коэффициентами регрессии.

Однако коэффициенты регрессии зависят от единиц измерения, и поэтому оказывается невозможно прямо сравнить два коэффициента для различных переменных, если они неодинаково измерены. Отсюда вытекает трудность в получении сравнительных оценок действий объясняющих (причинных) переменных на объясняемую. Если, однако, переменные нормированы путем деления на стандартное отклонение, то мы получим стандартизованные коэффициенты регрессии, которые дают возможность прямого сравнения действий независимых переменных на зависимые. Это свойство и нашло широкое применение в моделях причинного анализа. (Однако тут же необходимо отметить, что стандартизованный коэффициент регрессии является функцией дисперсий зависимых и независимых переменных, что невыгодно отражается на его свойствах.) Введем стандартизованные переменные и коэффициенты следующим образом:

и ,

где – средняя i-й переменной; – стандартное отклонение i -й переменной[174].

Тогда уравнение (4) запишется в виде

Коэффициент будем называть коэффициентом зависимости. Такое название оправдано его толкованием как доли стандартного отклонения зависимой переменной (с соответствующим

знаком), непосредственно объясняемой фактором , т.е. доли, которую можно было бы получить, если бы вариация этого фактора была идентична его действительно наблюдаемой дисперсии при фиксированном уровне остальных, в том числе и неявного фактора и. Таким образом, измеряет прямое влияние на и если будет подтверждено, что рассматриваемый граф причинных связей соответствует реальности, то можно считать мерой причинного влияния на .

Простая система причинных связей дана на рис. 23.

Структурное уравнение имеет вид

Для оценки коэффициентов зависимости умножим обе части уравнения на (i = l, 2, 3) и, вычисляя математическое ожидание от обеих частей уравнения, получим

.

Поскольку стандартизованы, математические ожидания будут равны коэффициентам корреляции, т.е. .Величины и равны нулю, по предположению о некоррелированности

и с независимыми переменными и .

Таким образом, мы получаем простой способ нахождения соотношений для коэффициентов зависимости. Для нашего примера найденные уравнения имеют вид

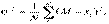(5)

(6)

(7)

причем , , вычисляются из наблюдаемых данных. Уравнения (5) – (7) называются системой оценочных уравнений для коэффициентов зависимости. Из анализа этих уравнений можно сделать следующие выводы:

а) решая систему оценочных уравнений, найдем

.

Сравнение этой оценки и оценки для уравнения (4) по методу наименьших квадратов показывает[175], что они эквивалентны. Этот результатверен и для n- мерногослучая;

б) рассмотрим уравнение (5) из оценочной системы:

.

Корреляцию между объясняемой и объясняющей переменной можно интерпретировать как сумму прямого воздействия () и косвенного (). Отсюда очевидна недостаточность выводов на основе одних лишь парных корреляций. Поскольку измеряет действие на при фиксированных остальных переменных, – прямое действие на , то за счет корреляции и парный коэффициент корреляции может существенно искажать выводы; может быть близок к нулю при разных знаках и , однако реальное действие переменной на будет велико. Интерпретируя таким образом формулу (5), не следует забывать, что вся эта интерпретация имеет смысл лишь по отношению к постулируемой причинной структуре;

в) находя из оценочной системы уравнений, нетрудно показать, что выражается через коэффициент множественной корреляции, т.е.

г) для графа связей с п независимыми переменными общие формулы имеют вид, аналогичный вышеприведенным, и не нуждаются в пояснениях.

В общем случае граф причинных связей включает не одну, а несколько объясняемых переменных z₁... z_n и описывается системой линейных уравнений (3).

Пусть, как и раньше, переменные стандартизованы. Задача состоит в поиске условий, при которых параметры системы могут быть определены из наблюдаемых данных.

Важный класс систем, который имеет особую значимость для описания причинных структур, составляют так называемые рекурсивные системы, у которых матрицы коэффициентов треугольны, т.е.

Если предположить, что u_i, не коррелируют между собой, т.е. и не коррелируют с независимыми переменными, то рекурсивная система идентифицируема. Кроме того, к каждому уравнению может быть применена оценка по методу наименьших квадратов.

Система рекурсивных уравнений определяет однонаправленный причинный процесс — процесс, не содержащий явление взаимодействия следствия и причины. Этому случаю, очевидно, отвечает состояние динамического равновесия объектов исследования. И наоборот, если постулируемую систему связей рассматривать как однонаправленный процесс, то он может быть списан рекурсивной системой уравнений.

Для иллюстрации рассмотрим конкретный пример.

Проблема состоит в том, чтобы объяснить зависимую переменную — занятие домашним трудом z ₉ — из ограниченного числа социально-демографических показателей. В частности, объяснение проводилось через такие характеристики, как пол (z ₂), возраст (z ₃), образование (z ₄), профессия (z ₅), заработная плата (z₆), семейное положение (z₇), наличие детей (z₈) и район проживания (z ₁).

В ходе исследования были сформулированы две альтернативные гипотезы относительно структуры причинных связей между рассматриваемыми признаками. Структура св язей, получившая в конечном счете эмпирическое подтверждение, изображена на

рис. 24 (такую сложную структуру удобнее записывать в виде матрицы коэффициентов).

Система структурных уравнений имеет следующий вид:

Оценочные уравнения получаются путем применения вышеописанной процедуры последовательно к каждому уравнению

системы. Заметим, что число получаемых оценочных уравнений здесь равно 33, а неизвестных коэффициентов — 24 (мы не рассматриваем уравнения для неявных факторов, поскольку они не влияют на оценку коэффициентов зависимости между явными переменными).

Переопределенную оценочную систему можно решить либо просто, как систему уравнений, либо — и это дает лучшее приближение к эмпирическим данным — методом наименьших квадратов. Полученные оценки повторной подстановкой в оценочные уравнения позволяют вычислить теоретические величины коэффициентов корреляции и путем их сравнения с эмпирическими проверить адекватность модели.

В табл. 15 приведены численные значения коэффициентов p_ij, а также эмпирические и теоретические величины коэффици-

Таблица 15

№ связи p_ji Коэффициенты корреляции № связи p_ji Коэффициенты корреляции

теоретические эмпирические теоретические эмпирические

0, 0814 0, 1653 0, 0142 —0, 0866 0, 11 0, 1

0, 262 0, 2587 0, 263 —0, 562 0, 0375 0, 0143

0, 255 0, 10 0, 1326 0, 821 0, 4355 0, 4454

—0, 106 0, 073 0, 0748 0, 314 0, 3684 0, 3305

ентов корреляции r_ij для связей объясняемого признака z₉ с объясняющими факторами z₁,... z₉ [176]

По таблице можно проследить не только соотносительные силы влияния каждой из переменных на объясняемый признак, но и учесть перераспределение этого влияния по всем постулируемым связям. Например, поскольку прямое влияние переменной z₁, на z₉ при фиксированных остальных измеряется величиной p_ji, а совместное действие всех переменных—коэффициентом корреляции r_ji, то разность (r_ji_–p_ji)является мерой влияния переменных на z_j, т.е. мерой общего косвенного воздействия этих переменных. Причем из оценочных уравнений можно вычислить опосредованное влияние каждой отдельной связи.

В общем случае модель изучаемой структуры связей может включать любое число объясняемых и объясняющих переменных при условии, что система структурных уравнений остается рекурсивной.

Заключение

Вся история конкретных социологических исследований в СССР за последние десять лет была связана со все более широким и более специализированным использованием математических методов сбора и обработки первичной социальной информации.

В первых конкретных социологических исследованиях при анализе социальных данных были взяты на вооружение простейшие математические и статистические методы — методы средних чисел, метод аналитических группировок, индексовый метод анализа, т.е. методы так называемой дескриптивной статистики.

По мере развития конкретных социологических исследований применялись все более точные математические методы анализа социальных данных и выборки. Оперирование с большими массивами социальной информации привело к проблеме использования вычислительной техники — счетно-перфорационных и электронно-вычислительных машин. Социологи-марксисты столкнулись с необходимостью измерения качественных социальных переменных и моделированием социальных процессов и явлений. В настоящее время перед марксистско-ленинской социологией стоит задача разработки методов измерения самых различных систем социальных показателей и индикаторов народнохозяйственного планирования, создания комплексных математических социально-экономических моделей и т.д.

Однако применение математики в исследовании некоторых социологических проблем, например проблем социальной структуры общества, пока идет в социально-экономическом направлении. Количественно изучается влияние материальных показателей: доход, заработная плата, жилая площадь, число школ, больниц, киноустановок и т.п. Все это, естественно, необходимо. Это — основа. Но вместе с тем необходимо смелее изучать соб-

ственно человека и переменные, характеризующие его развитие изучать его социальные потребности, интересы и отношения в группах и территориальных общностях: его желания, мнения установки, ориентации, симпатии, удовлетворенность жизнью национальные чувства, физическое и духовное здоровье, т.е. необходимо решать проблему измерения в собственно социологических и социально-психологических аспектах исследования.

Ярким примером использования математики в социальных науках является экономика. Образец построения количественной модели экономики мы находим у К. Маркса, который во втором томе «Капитала» дал схемы расширенного производства. В настоящее время разработка проблем применения математических методов в экономике, внедрение количественных способов анализа экономических явлений не только обогащает экономическую теорию, но и стимулирует развитие самой математики[177]. Интересную мысль в отношении специфики использования математических методов в социальных науках высказали выдающийся математик современности Дж. фон Нейман и американский экономист О. Моргенштерн — авторы классической книги «Теория игр и экономическое поведение»: «Решающая фаза применения математики к физике — создание Ньютоном науки механики — происходила и едва ли могла быть отделена от открытия исчисления бесконечно малых. (Имеется еще несколько примеров, но ни один из них не сильнее этого.) Важность социальных явлений, богатство и множественность их проявлений по меньшей мере равны физическим. Следовательно, надо ожидать — или опасаться, — что потребуются математические открытия того же ранга, что исчисление бесконечно малых для того, чтобы произвести решительный переворот в этой области... невероятно,.что только повторение приемов, которые так хорошо служили в физике, даст что-то ценное для социальных явлений. В самом деле, вероятность очень мала, так как мы покажем, что в нашем обсуждении сталкиваемся с математическими задачами, которые совершенно отличны от задач, встретившихся в физике. Нужно иметь в виду эти наблюдения в связи с современным преувеличением роли математического анализа, дифференциальных уравнений и т.д. в качестве главных орудий математической экономики»[178].

Чрезвычайно важная задача — разработка и развитие специфических органически возникших из потребностей социологии.

математических методов. В этой связи хотя бы в заключении мы не можем не упомянуть о важной группе методов — так называемых методах многомерного шкалирования, которые создаются и развиваются в процессе решения собственно социологических и психологических задач.

Представляет интерес то, что «методы многомерного шкалирования» сводятся к новым направлениям в области измерения в социологии и психологии. Эти методы имеют свои истоки в физике и психофизике. Как известно, звук можно рассматривать в одном измерении, например только по громкости или только по высоте. А можно определить сразу два этих параметра и соответственно найти точку в двухмерном пространстве. Этот вопрос возникает иимеет большое значение, когда нет предварительных сведений о числе измерений данного стимула или суждения. Например, мы спрашиваем «нравится — не нравится?», «красивая вещь или некрасивая?», «почему вещь нравится или кажется красивой?». И каждый ответ будет самостоятельным измерением красоты и привлекательности. Это связано с проблемой эквивалентности стимулов, что имеет большое распространение в изучении восприятия, мышления, обучения и измерения установок.

Предположим, что мы имеем четыре суждения — ABCD, которые зависят от двух измерений D₁ и D₂. Если бы мы могли их изолировать, то могли бы сначала определить координаты ABCD по измерению D₁, а затем (изолируя D₁ ) —координаты по измерению D₂. Но это не всегда можно сделать, и если это сделать нельзя, то используют расстояния между стимулами. Эти расстояния выражают степень подобия или различия.

Если обнаружится, что АВ + BC = АС, то можно считать, что имеет место одно измерение. Если АВ+ВС > АС, то имеет место два измерения. Три стимула могут быть расположены в пространстве не больше двух измерений (три точки определяют плоскость), четыре стимула могут быть в пространстве одного, двух, трех измерений. Наименьшее число измерений, в котором расположены все расстояния, и будет размерностью этого множества суждений (стимулов).

Л. Ричардсон в 1938 г. впервые для решения проблемы многомерного шкалирования ввел метод триад. Стимулы представляются группами по три, и в каждой группе надо определить, какие два стимула — самые близкие и какие — наиболее различаются. Эти три расстояния ранжируются. Затем применяется парное сравнение не к стимулам, а к расстояниям и соответственно применяется закон сравнительного суждения к расстояниям.

Позднее У. Торгерсонрасшил идеи Л. Ричардсона и тогда этот подход получил название метода многомерного шкалирования. Существенно, что в работах Ричардсона — Торгерсона размерность исследуемого явления определяется из рассмотрения совокупности эвклидовых расстояний между исходными стимулами-суждениями. Р. Шеппард, а затем Краскал начали использовать в качестве исходных данных не эвклидовы расстояния, а различные качественные меры близости между объектами. По своей сути подход Ричардсона-Торгерсона — метрическое многомерное шкалирование, а подход Шеппарда-Краскала — неметрическое многомерное шкалирование.

Работа по применению математических методов в социологии развивается в четырех направлениях: во-первых, это решение проблем методологии социологического исследования, а именно: выборки, анализа данных, измерения и моделирования; во-вторых, это расширение сферы и отраслей социологического знания, в которых возможно использование математических методов; в-третьих, это увеличение количества средств и методов и их модификаций из всевозможных разделов математики; и, наконец, это поиск на пути создания собственных математических методов в социологии. Эти четыре направления представляют единый процесс — ни одно не существует вне других. Действительно, поиск нового собственно социологического математического формализма происходит не абстрактно, а на базе уже имеющегося аппарата, необходимого в определенной области социологии и одновременно в ходе решения одной из методологических проблем социологического исследования — выборки, анализа данных, измерения или моделирования. Наконец, если мы возьмем, например, выборку или моделирование, то они осуществляются посредством уже имеющихся и апробированных математических средств во многих отраслях социологии и, естественно, для них возможен поиск новых путей.

Проникновение математики в социологию, в особенности в конкретные социальные исследования, происходит все более интенсивно, хотя и сопряжено с реальными ощутимыми трудностями. Одно из условий преодоления этих трудностей — их выявление и тем самым привлечение к ним внимания и математиков, и социологов. Совместная работа социологов и математиков, которая уже началась в нашей стране, будет содействовать развитию применения математики в социологии, выработке математических методов, специфических для социологии, и в частности методов социологического измерения.

[1] Маркс К. и Энгельс Ф. Соч., т. 19, с.350-351.

[2] Ленин В. И. Полн. Собр. Соч., т. 1, с.139

[3] Там же, с. 140

[4] Там же, с. 429.

[5] Маркс К. и Энгельс Ф. Соч., т.19, с. 573.

[6] Маркс К. и Энгельс Ф. Соч., т.2, с.235.

[7] Ленин В. И. Полн. Собр. Соч., т.30, с.13

[8] Ленин В. И. Полн. Собр. Соч., т.36, с.372

[9] Маркс К. и Энгельс Ф. Соч., т.3, с.25.

[10] Маркс К. и Энгельс Ф. Соч., т.39, с.175

[11] Федосеев П. Н. Коммунизм и философия. М., 1971, с.417

[12] Рабочая книга социолога. М., 1976, с.15

[13] См., например: The Nature and Scope of Social Sciences. L. D. Krimerman (Ed.). N.Y., 1969

[14] Timasheff N.S. Sociological theory. Its nature and growth. N. Y., 1955, p.191.

[15] См., например: Filmer P., Phillipson M., Silverman D., Walsh D. New Directions in Sociological Theory. London, 1972.

[16] Popper K. Unity of method on the nature and social sciences. – In: Philosophical Problems of the Social Sciences. D.Braybrocke (Ed.). N.Y., 1965.

[17] Lundberg J. The Natural Science Trend in Sociology. – «Amer. J. Sociol.», 1955, N 61, p. 191

[18] Ibit., p. 192.

[19] Конт О. Курс положительной Философии, т. 2 СПб., 1900, с.7.

[20] См., например: Беккер Г., Босков А. Современная социологическая теория. М., 1961, с.222—228.

[21] Конт О. Курс положительной философии, т. 1. СПб., 1900, с.6.

[22] Hempel C. Foundation of Concept Formation in Empirical Sciences. – In: International Encyclopedia of Unified Science, v. 2, N 7, Chicago, 1952; Zetterberg H. On Theory and Verification in Sociology. N. Y., 1965; Lundberg G.A. Social Research. A Study in methods of Gathering Data. N.Y., 1968; Greer S. The logic of Social inquiry. Chicago, 1969.

[23] Lazarsfeld P. F. The logical and mathematical foundation of latent structure analysis. – In: Measurement and Predictions, v. 4. N. Y., 1950; Boudon R. A new look at correlation analysis. – In: Methodology in Social Research. H. Blalock and A. Blalock (Eds). N. Y., 1968; Causal models in social sciences. H. Blalock (Ed.). N. Y., 1971.

[24] Dood S. Deminsions of society. N. Y., 1942; Zipf K. Human behaviour and the principles of least efforts. N. Y., 1949; Rashevsky N. Mathematical biology of social behaviour. Chicago, 1951; Rapoport A. Fights, games and debates. Ann Arbor, 1960; Coleman J. S. An introduction to mathematical sociology. N. Y., 1964; Fararo J. mathematical sociology. N. Y., 1973.

[25] Рашевский Н. Две модели: подражательное поведение и распределение статуса. – В кн.: Математические методы в современной буржуазной социологии. М., 1966, с. 190

[26] Marschak J. Toward and economic theory of organization and information. – In: decision Processes. R. Thrall e.a. (Eds). New York – London, 1954, p. 187.

[27] Петти В. Политическая арифметика. – В кн.: Экономические и статистические работы. М., 1940, с.156

[28]

[29] Петти В. Пять ответов по политической арифметике. – В кн.: Экономические и статистические работы, с. 259.

[30] Вагнер А. История и теория статистики.— В кн.: История и теория статистики. Под ред. Ю. Янсова. СПб., 1879.

[31] Маркс К. и Энгельс Ф. Соч., т.32, с.495-496.

[32] Лаплас П. Опыт философии теории вероятностей. М., 1908, с.65

[33] Кетле А. Социальная физика, т.1. Киев, 1912, с.13

[34] Маркс К. и Энгельс Ф. Соч., т.23, с.6.

[35] Ленинский сборник ХХХ, с. 303.

[36] Ежов А. И. Организация статистики в СССР. М., 1968, с. 131-133.

[37] Винер Н. Кибернетика. М., 1958, с. 201-202.

[38] Ленин В.И. Полн. Собр. Соч., т.25, с.41.

[39] Глушков В. М. О гносеологических основах математизации наук. М., 1965, с.6.

[40] Kendall M. G. Natural Law in the Social Science. – “J. Roy. Stat. Soc. Ser. A”, 1961, v. 124, p.1.

[41] Наиболее ярко недостатки такого рода проявились в книге «Моделирование социальных процессов» (М., 1970) и в этой связи подверглись справедливой критике научной общественностью.

[42] Стивенс С. Экспериментальная психология, т.1. М., 1960, с. 24-25.

[43] Фишер И. Построение индексов. М., 1928, с. 30

[44] См. также: Казинец Л.С. Теория индексов. М., 1968.

[45] Кедров Б.М. Категории материалистической диалектики как методологическая основа статистической науки.—В кн.: Ученые записки по статистике, т. 6. М., 1961.

[46] Ракито А.И. Предмет, структура и гносеологическая функция статистики.—В кн.: Некоторые проблемы методологии научного исследования. М, 1965.

[47] Статистика в социологических исследованиях. М., 1965.

[48] Немчинов В. С. Социология и статистика. — В кн.: Социология в СССР, т. 1. М., 1966.

[49] Маслов П. П. Бюджет времени. — В кн.: Ученые записки по статистике, т. 6; он же. Статистика и ее роль в конкретно-социологических исследованиях.— В кн.: Вопросы организации и методики конкретно-социологических исследований. М., 1963; он же. Социальные методы.—В кн.: Социология в СССР, т. 1.

[50] Андреев Э. П., Осипов Г. В. Математика и социология.—«Вопросы философии», 1968, № 11.

[51] Measurement and Prediction, v. 4. S. Stouffer (Ed.). Princeton, 1950.

[52] Stouffer S. Quantitative methods. – In: Review of Sociology. J. B. Gittler (Ed.). N. Y., 1957.

[53] См., например: Количественные методы в социологии. М., 1966; Шубкин В. Н. Количественные методы в социологии. — «Вопросы философии», 1967, №3.

[54] Патрушев В.Д. О некоторых вопросах выборки в социологических исследованиях.— В кн.: Научный семинар по применению количественных методов в социологии, вып. 2. М., 1966.

[55] Осипов Г.В. и др. Задачи и методы конкретных социологических исследований.—В кн.: Вопросы организации и методики конкретно-социологических исследований. М., 1963; Грушин Б. А. К проблеме качественной репрезентации и выборочном опросе.— В кн.: Опыт и методика конкретных социологических исследований. М., 1965.

[56] Человек и его работа. Социологическое исследование. М., 1969.

[57] Елкина В.Н., Загоруйко Н.Г. Алгоритмы таксономии.—В кн.: Распознавание образов в социальных исследованиях. Новосибирск, 1968.

[58] Воронов Ю.П. Распознавание образов и выборка в социологических исследованиях. — В кн.: Социология и математика. М., 1970.

[59] Количественные методы в социологии; Методика и техника статистической обработки первичной социологической информации. М., 1968; Суслов И. П., Гражданников Е. Д. Основы социальной статистики. Новосибирск, 1975.

[60] Заславская Т.И. Использование методов факторного анализа для изучения миграции сельского населения.— В кн.: Научный семинар по применению количественных методов в социологии, вып. 1, Новосибирск, 1964; Говорущенко В., Кахк Ю. и др. Опыт применения корреляционного и факторного анализа в социологическом исследования межнациональных отношений. — В кн.: Количественные методы в социальных исследованиях. Информ. бюлл. ИКСИ АН СССР, вып. 9. М., 1968; Заславская Т. И., Виноградова Е. В. Опыт математи-статистического исследования закономерностей мобильности трудовых ресурсов. — В кн.: Социальные проблемы трудовых ресурсов села. Новосибирск, 1968.

[61] Таганов И. Н,, Шкаратан О. И. Исследование социальных структур методом энтропийного анализа.— «Вопросы философии», 1969, № 5; Докторов Б. 3. Регрессивно-факторная модель и задача прогнозирования. Доклад на VII МСК в г. Варне. М., 1970.

[62] Загоруйко Н. Г. Классификация задач распознавания образов. — В кн.: Вычислительные системы, вып. 227. М., 1966; Лбов Г. С. Алгоритмы эффективной системы признаков.— В кн.: Распознавание образов в социальных исследованиях; Заславская Т. И., Мучник И. Б. Об одном методе классификации объектов в социологии. — «Социологическое исследование», 1974, № 1.

[63] Контентный анализ. Новосибирск 1970; Методологические и методические проблемы контент-анализа, вып. 1-2. Новосибирск, 1973.

[64] Количественные методы в социальных исследованиях. Информ. бюлл. ИКСИ АН СССР, вып. 9

[65] Turkey J.W., Wilk M.B. Data Analysis and Statistics: Techniques and Approaches. – In: Quantitative Analysis of Social Problems. E.R. Tufte (Ed.). N.Y., 1970

[66] Шляпентох В.Э. Проблемы достоверности статистической информации в социологических исследованиях. М., 1973

[67] Coombs C.A. Theory of Data. – “Psychol. Rev.”, 1960, v. 67, p. 143

[68] Устинов В.А., Деев Л.Ф. Опыт применения ЭВМ в социологических исследованиях. Новосибирск, 1967.

[69] Розин Б.Б., Стролко Р. и др. Разработка материалов массовых наблюдений на счетно-перфорационных и электронно-вычислительных машинах. – В кн.: Количественные методы в социологии.

[70] Маслова Л.Н., Патрушев В.Д. О возможностях исследования счетно-перфорационных машин для обработки материалов социологических исследований. – В кн..: Научный семинар по применению количественных методов в социологии, вып. 2

[71] Молчанов В.И. Применение ЭВМ в социологическом исследовании. – «Социологические исследования», 1974, № 1.

[72] Анализ социологической информации с применением ЭВМ, Ч. 1-2. М., 1976.

[73] Программа обработки первичной социологической информации на ЭВМ. - В кн.: Методика и техника статистической обработки первичной социологической информации.

[74] Кваша В.В., Велшкшй А.И. Об одном опыте прогнозирования численности и структуры семей. - В кн.: Моделирование социальных процессов; Гражданников Е.Д. Прогностические модели социально-демографических процессов. Новосибирск, 1974.

[75] Кудрявцев В.Н. Причинность в криминологии. М., 1968.

[76] Герасимов Т. Теория игр и международные отношения - «Мировая экономика и международные отношения», 1966, № 7.

[77] Амосов Н.И., Галенко Д.Н. О моделировании социального взаимодействия в малых коллективах. – В кн.: Количественные методы измерения в социологии. Информ. бюлл. ИКСИ АН СССР, вып. 8.

[78] Гаврилец Ю.Н. Некоторые вопросы количественного изучения социально-экономических явлений «Экономика 11 математические методы», 1969, т. 5, вып. 5; он жe. Социально-экономическое планирование. Системы и модели. М., 1974.

[79] Аганбегян А.Г., Шубкин В Н. Социальные исследования и количественные методы. - В кн.: Количественные методы в социологии, с. 25.

[80] Маслов П.П. Статистика в социологии. М., 1971, с. 1935.

[81] Моисеев Н.Н. Математик задает вопросы М, 1974, с. 35.

[82] Аганбегян А.Г. Некоторые особенности применения математических моделей в социологических исследованиях. - В кн.: Моделирование социальных процессов.

[83] Шубкин В.Н. Социологические опыты. М., 1970, с. 215-221.

[84] Количественные методы в социологии, с. 224-231

[85] Гаврилец Ю.Н. Социально-экономическое планирование…, с. 70

[86] Гаврилец Ю.Н. Социально-экономическое планирование…, с. 76

[87] Гаврилец Ю.Н. Социально-экономическое планирование…, с. 77

[88] Андреева Г.М. Современная буржуазная эмпирическая социология. М., 1965; Самсонов Ю.Б. Некоторые проблемы социологического измерения. -.В кн.: Моделирование социальных процессов; Измерение и моделирование в социологии. Новосибирск, 1969.

[89] Гельмгольц Г. Счет и измерение. Казань, 1893.

[90] Hö lder O. Die Axiome der Quantitä t und die Lehre von Ma. – „Ber. Sä chsisch. Ges. Wiss. Math.-phys. Kl.”, 1901. Bd. 53, S. 1-64

[91] Лебег А. Об измерении величин. М., 1960, с. 104

[92] Campbell N.R. Physics: the elements. London, 1920; Campbell N.R. An account of the Principles of measurement and calculation: London, 1928.

[93] Ле6ег А. Об измерении величин, с. 9.

[94] Oмельяновский М.Э. Философские основы теории измерения. Автореф. докт. днсс.. 1943.

[95] Russel В. The Principles of Mathematics. London, 1937. р. 167.

[96] Маликов М.Ф., Тюрин Н.Н. Введение в метрологию. М., 1965, с. 21

[97] Омельяновский М.Э. Диалектика в современной физике. М., 1973, с. 227.

[98] Campbell N.R. An account pf the principles of measurement and calculation, p. 5

[99] Krantz D. A survey of measurement theory. – In: Mathematics pf the Decision Science, pt. 2. G. Dakotzig (Ed,), p.315

[100] Соотbs С. А theory of psychological Sealing. Michigan, 1952, р. 12.

[101] Coombs C. Theory and methods of Social Measurement. – In: Research Methods in the Behavioral Sciences. L. Festinger (Ed.). N.Y., 1954, p. 472

[102] Стивенс С. Экспериментальная психология, т. 1, с. 51

[103] Ядов В.А. О некоторых приемах и методах исследований в области пропаганды В кн.: Проблемы научного коммунизма, вып. 2. М., 1968.

[104] Coombs C.H. A Theory of psychological Scaling. – “Ending Res. Bull.”, 1952, p. 34

[105] Суппес П., Зиннес Дж. Основы теории измерений. – В кн.: Психологические измерения. М., 1967.

[106] Torgerson W. Theory and Methods of Sealing. N.Y., 1958

[107] Осипов Г.В., Андреев Э.П. Вопросы измерения в социологии. – В кн.: Количественные методы в социальных исследованиях. Информ. бюлл. ИКСИ АН СССР, вып. 8

[108] Воронов Ю.П., Ершова Н.П. Общие принципы социологического измерения. В кн.: Измерение и моделирование в социологии

[109] Осипов Г. В. Вступительная статья в кн,: Математические методы в современной буржуазной социологии. М., 1966

[110] Количественные методы в социальных исследованиях. – Информ. бюлл. ИКСИ АН СССР, вып. 8

[111] Человек и его работа.

[112] Здравомыслов А.Г., Докторов Б.З. Альтернативная оценка структурных элементов как прием социологического исследования. – «Количественные методы в социальных исследованиях. Бюллетень ССА», 1968, №9.

[113] Патругин Ю.А. Об измерении качественных признаков. – В кн. Моделирование социальных процессов.

[114] Мартынова Н.В. О многомерном измерении в социологии. – «Философские науки», 1970, № 5.

[115] Осипов Г.В., Андреев Э.П. Математика и социология. – В кн.: Социальные исследования, вып. 2, М., 1970

[116] Айзерман М.А., Браверман Э.М., Розоноэр Л.И. Вероятностная задача об обучении автоматов распознавания классов и метод потенциальных функций. – «Автоматика и телемеханика», 1964, т. 25, №9.

[117] Комаровский В. С. Некоторые проблемы измерения социальных установок. – «Вопросы философии», 1970, №7.

[118] Калмык В.А., Бородкин Ф.М., Спесивцев И.Н. Об оценке привлекательности профессий. – В кн.: Социальные исследования. Вопросы методологии. Новосибирск, 1966.

[119] Blalock H.M. Social Statistics. N.Y., 1960; Кэнделл Д. и М. Теория статистики. М., 1960; Уилкс С. Математическая статистика. М., 1967; Ferguson G.A. Statistical Analysis in Psychology and Education. N.Y., 1966.

[120] Венецкий И.Г., Кильдишев Г.С. Основы теории вероятностей и математи ческой статистики. М., 1968, с. 55.

[121] Гнеденко Б.В. Курс теории вероятностей. М., 1965, с. 37.

[122] Вентцель Е.С. Теория вероятностей. М., 1969, с. 81

[123] Гнеденко Б. В. Курс теории вероятностей. М.— Л., 1950, с. 273.

[124] Варден В. дер. Математическая статистика. М., 1960, с. 307. 76

[125] Дунин-Барковский И., Смирнов Н. Теория вероятностей и математическая статистика в технике. М., 1955, с. 360.

[126] См.; например: Романовский В. И. Математическая статистика, кн. 1 — 2. Ташкент, 1961.

[127] Романовский В. И. Элементарный курс математической статистики. М.— Л, 1939, с. 225 — 228.

[128] Романовский В. И. Элементарный курс математической статистики, с. 234

[129] Слуцкий Е. Е. Теория корреляции и элементы учения о кривых распределения. Киев, 1912, с. 85.

[130] Романовский В. И. Элементарный курс математической статистики, с. 272- 281.

[131] Там же, с. 276.

[132] Бернстайн А. Справочник статистических решений. М., 1968, с. 92.

[133] Gulliksen Н. Theory of Mental Tests. N. Y., 1950, р. 2.

[134] См.: Guilford 1. P, Psychometric Methods N. Y., 1954, р. 233.

[135] Garner W., Creelman С. Problems and methods of psychological scaling.—In: Attitude Measurement. G. Summers (Ed.). Chicago, 1970.

[136] Thurstone L. L. A law of comparative judgement.— «Psychol. Rev.», 1927, v. 34, p. 273.

[137] Scott W. A. Attitude measurement.— In: Handbook of Social Psychology, v. 2. G. Lindzey, E. Aronson (Eds). N. Y., 1968.

[138] Coombs С.A Theory of Data. N. Y., 1964.

[139] Coombs С.A Theory of Data.— «Psychol. Rev.», 1960, N 67, p. 143.

[140] Downie N. M. Foundamentals of Measurement. N. Y., 1967.

[141] Bogardus E. S. Immigration and Race Attitudes. Boston, 1928; Bogardus E. S. The Development of Social Thought. N. Y., 1960; Social Problems and Social Processes. E. S. Bogardus (Ed.). N. Y., 1967.

[142] Ядов В. А. Социологическое исследование. Методология, программа, методы. М., 1972, с.109.

[143] Likert R., Roslow S., Murphy G. A simple and reliable method of scoring the thurstone attitude scales.—«J. Social Psychol.», 1934, v. 5.

[144] Ferguson L. W. The measurement of primary social attitudes. — «J.Psychol.», 1940, v. 10, p. 199; Ferguson L. W. A study of the Likert technique ofattitudescale construction.— «J. Cocial Psychol.», 1941, v. 13, p. 51.

[145] Edwards А. L., Kenney К. С. A comparison of the Thurstone and Likert techniques of attitude scale construction.— «J. of Applied Psychol.», 1946, v.30, p. 72; Edwards A. L., Kilpatrick F. P. A technique for the construction of attitude scales—«J. Psychol.», 1948, v. 32, p. 374.

[146] Волков И. П. Социометрические методы в социально-психологических исследованиях. Л., 1970.

[147] Кемени Дж., Снелл Дж., Томпсон Дж. Введение в конечную математику М., 1963, с. 415.

[148] Semantic differential technique. J. G. Snider, С. Е. Osgood (Eds). Chicago 1969, p. 26.

[149] Osgood С. Е., Suci G. J., Tannenbaum P. H. The measurement of meaning. Urbana, 1957.

1818 Guilford J. P. Psychometric Methods. N. Y., 1954.

1919 Guilford J. P. Psychometric methods, p. 353.

2020 Ibid., p. 380.

[150] Anderson T. W. Some scaling models and estimation proceduces in the latent class model.— In: Probability and Statistics. U. Grenander (Ed.). Stockholm — New York, 1959.

[151] Spearman S. General intelligence objectwely determined and measured, — «Amer. J. Psychol.», 1904, N 15, p. 201—293.

[152] Thurstone L. L. Multiple factor analysis. Chicago, 1947.

[153] Kendall M. G., Smith В. В. Factor Analysis as Statistical technique.— «J. Roy. Statist. Soc. B», 1950, v. 12, p. 60.

^{^[154]}⁵ Лоули Дж., Максвелл А. Факторный анализ как статистический метод. М., 1967, с. 136.

[155] Bell W. Economic, Family and Ethnic Status: an Empirical Test.— «Amer. Soc, Rev.», 1955, v. 20, p. 45.

[156] Price D. О. Factor Analysis in the Study of Methropoliten Centres.—«Social Forces», 1942, v. 20, N 4, p. 449.

[157] Moser С., Scott W. British Town. Edinburgh — London, 1961.

^{^[158]}⁹ Количественные методы в социальных исследованиях.— Информ. бюлл. ИКСИ АН СССР, вып. 9.

М., 1968, с. 34.

[159] Социальные проблемы трудовых ресурсов села. Под ред. Т. И. Заславской. Новосибирск, 1968,

с. 107— 124.

[160] Социальные проблемы трудовых ресурсов села, с. 116.

[161] Cattel R. В. Personality and Social Psychology. San Diego, 1964.

[162] Horst P. Factor analysis of data matrices. N. Y., 1965, p. 142.

[163] Lazarsfeld P. F. The logical and mathematical foundation of latent structure analysis. – In: Measurement and Prediction. N. Y., 1950.

[164] Lazarsfeld P.F., Henry N.W. Latent Structure Analysis. N. Y., 1968.

[165] Петров Ю. А. Логическая функция категорий диалектики. М ., 1972, с. 52.

[166] Wold Н. Econometric as Pioneering in Nonexperimental Modelbuilding.— «Econometrica», 1969, v. 37, р. 319.

[167] Wold H. Causality and Econometrics.— «Econometrica», 1954, v. 22, р. 162.

[168] Подробности см. в специальной литературе, например: Тинтнер Г. Введение в эконометрику. М., 1965.

[169] Wright S. Соггelаtiоn аnd саusа1itу. – «J. Agric. Res.», 1921, v. 20, р. 557.

[170] Simon Н. Spurious Correlation: а Causal Interpretation. – «J. Amer. Statist. Assoc.», 1954, v. 49, р. 467.

[171] Поскольку измерения производятся с ошибкой, то, очевидно, приблизительно будет равен нулю, и следовательно, тождество (2) будет выполнятьсятакже лишь приблизительно.

[172] Ficher F. The Indentification Problem in Econometrics. N. Y., 1966.

[173] Основные идеи метода измерения причинных связей изложены в ранних работах С. Райта, а наиболее полно – в статье «Корреляцияипричинность» (Wright S. Correlation and i Causality. – «J. Agric. Res.», 1921, v. 20, р. 557).

[174] Использование коэффициентов для анализа причинных связей впервые было изучено С. Райтом, который назвал их «path-коэффициентами». Это названиезакрепилось в американской литературе, и, более того, вся процедура исследования причинных связей с использованием этих стандартизованных коэффициентов получила это название.

[175] См., например: Кендэл М., Стюарт А. Статистические выводы и связи. М., l973, гл. 27.

[176] Нереесова Е. X. Выбор модели изучаемого явления методом зависимости.— В кн.: Динамика изменения положения женщин и семья. М., 1972, с. 114 (в работе Нерсесовой использован дихотомический аналог r_ij—Ф_ij).

[177] Федоренко Н. П. Экономика и математика. М., 1967, с. 13

[178] Нейман Дж. фон, Моргенштерн О. Теория игр и экономическое поведение. М., 1970, с. 7—9.

⇐ Предыдущая 8 9 10 11 12 13 14 15 1617

Поделиться с друзьями:

mylektsii.su - Мои Лекции - 2015-2024 год. (0.101 сек.)Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав Пожаловаться на материал