
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
А:в] – полуоткрытые интервалы
|
|
R- множество действительных чисел. Оно состоит из рациональных и ироциональных чисел.
Рациональные числа можно выразить в виде конечной или бесконечной периодической десятичной дроби. ¼ = 0, 25 1/3=0, 333
Числа, не являющиеся рациональными называются- ироциональными. Их представляют в виде бесконечно не периодической десятичной дроби.
Введение множества комплекстных чисел связано с тем, что в множестве действительных чисел не выполняется извлечение корня четной степени из отрицательного числа. Комплекстным числом z – называют упорядоченную пару чисел x: y
Алгебраическая формула комплекстного числа z=x+iy. Где x- действительная часть, а y- мнимая часть, i- мнимая единица. Если x=0, то z=iy – число мнимое, если y=0, то z=x- действительное число.
Вопрос 2 «Числовые промежутки. Окрестность (.)
А, в действительные числа а< в. Числовыми промежутками (интервалами) называют подмножества всех действительных чисел имеющие следующий вид.
[a: в]={x: а< x< в}- отрезок
(а: в)={x: а< x< в}-интервал
А: в) –полуоткрытые интервалы
а: в] – полуоткрытые интервалы
(-бесконечность: в)= {x: x< в} – бесконечные интервалы
а, в называются левым и правым концами промежутка. Пусть Х0 любое действительное число в (.) на числовой прямой. Окрестностью (.) называют любой интервал (а: в) содержащий эту точку в частности интервал (Х0-Е: Х0+Е) Е> 0 – эпсилан окрестностью (.) Х0 число Х0- называют центром, эпсилан – называют радиусом.
21. Уравнение касательной и нормали
Если точка Мо (хо; уо) точка касания, то угловой коэффициент касательной = f '(xо) пользуясь уравнением прямой проходящую через точку Мо в заданном направлении к у-уо =К(х-хо)
Запишем уравнение касательной
У-уо = F '(ХО) (Х-ХО)
Прямая перпендикулярна касательной в точке в точке касания наз. Нормальной кривой в этой точке.
Она перпендикулярна касательной следовательно Кнорм= -1: Ккас (угл. Коэф)
Кнорм= -1: Ккас = -1: f '(хо)
У-уо= -1: -f '(хо)* (х-хо) уравнения норм. проходящей через точку Мо
(f '(х)не равна 0)
22. Правила дифференцирования
Пусть u=u(x) V=V(x)
1. (u плюс минус v)= u 'плюс минус v '
2. (uv) '=u 'v+v 'u, в частности (cu) '= cu ' то есть постоянную можно вынести за знак производной
3. (u: v) '= u 'v-v 'u: v в квадрате
4. Дифференцирование сложной функции
У= f(u) u=f(x)
Y 'x=Y 'u*U 'x
5. Если у=f(х) х=f(y) следовательно У 'х= 1: Х 'у
Задача о скорости движущейся точки.
Пусть s = s (t) представляет з акон прямолинейного движения материальной точки.
Это уравнение выражает путь s, пройденный точкой, как функцию времени t.
Обозначим через Δ s путь, пройденный за промежуток времени Δ t от момента t до t + Δ t, т. е.
Δ s = s (t + Δ t) - s (t). Отношение  называется средней скоростью точки за время от t до t + Δ t.
называется средней скоростью точки за время от t до t + Δ t.
Чем меньше Δ t, т. е. чем короче промежуток времени от t до t + Δ t, тем лучше средняя скорость характеризует движение точки в момент времени t. Поэтому естественно ввести понятие скорости v в данный момент t, определив ее как предел средней скорости за промежуток от t до t + Δ t, когда Δ t→ 0: 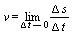
Величина v называется мгновенной скоростью точки в данный момент t.
Задача о касательной к данной кривой. Пусть на плоскости хОу дана кривая уравнением у = f (х). Требуется провести касательную к данной кривой в данной точке 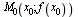 . Так как точка касания
. Так как точка касания  дана, то для решения задачи потребуется найти только угловой коэффициент искомой касательной, т. е. tg φ — тангенс угла наклона касательной к положительному направлению оси Ох (рис.).
дана, то для решения задачи потребуется найти только угловой коэффициент искомой касательной, т. е. tg φ — тангенс угла наклона касательной к положительному направлению оси Ох (рис.).
 Через точки
Через точки 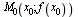 и
и  проведем секущую
проведем секущую  Из рис. видно, что угловой коэффициент tg α секущей
Из рис. видно, что угловой коэффициент tg α секущей  равен отношению
равен отношению  —, где
—, где
 Угловой коэффициент касательной
Угловой коэффициент касательной 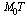 к данной кривой в точке
к данной кривой в точке  можно найти на основании следующего определения:
можно найти на основании следующего определения:
касательной к кривой в точке  называется прямая
называется прямая 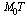 , угловой коэффициент которой равен пределу углового коэффициента секущей
, угловой коэффициент которой равен пределу углового коэффициента секущей  , когда
, когда  . Отсюда следует, что
. Отсюда следует, что

12. Первый и второй замечательные пределы
При вычислении переделов выражений содержащих тригонометрические функции часто используют предел  =1, который называется первым замечательным пределом.
=1, который называется первым замечательным пределом.
Рассмотрим предел  =e, заменим в этой формуле
=e, заменим в этой формуле  =
= 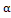 ;
; 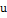 =
=  =>
=> 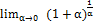 =e.
=e.
Эти 2 равенства называются вторым замечательным пределом.
11. Признаки существования пределов
Не всякая ограниченная функция имеет предел.
Например: y=sin x; x→ ∞ не имеет предела.
Для выяснения вопроса о существовании предела использование определения предела не всегда удобно. Проще это сделать с помощью признаков существования пределов.
1) о пределе промежуточной функции
Если функция f(x) заключена между функциями φ (x) и g(x) стремящимися к одному и тому же пределу, то она стремится к этому же пределу.
2) о пределе монотонной функции
Если функция f(x) монотонна и ограничена при x<  или при x>
или при x>  , то существует левый предел
, то существует левый предел 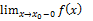 или правый предел
или правый предел 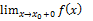 .
.
30. (Правило Лопиталя).
Пусть функции  и
и  удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
1) эти функции дифференцируемы в окрестности точки  , кроме, может быть, самой точки
, кроме, может быть, самой точки  ;
;
2)  и
и 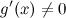 в этой окрестности;
в этой окрестности;
3)  ;
;
4) 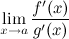 существует конечный или бесконечный.
существует конечный или бесконечный.
Тогда существует и  , причем
, причем 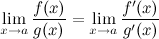
31. ФОРМУЛА ТЕЙЛОРА
В определении функции у=ƒ (х) не говорится о том, при помощи каких средств находятся значения у по значениям х. В тех случаях, когда функция является формулой вида у=х3/5-5х+7, значения функции найти легко с помощью четырех арифметических действий. Но как найти значения, например, функций у=sinx, у=ln(1+х) при любых (допустимых) значениях аргумента? Для того, чтобы вычислить значения данной функции у=ƒ (х), ее заменяют многочленом Рn(х) степени n, значения которого всегда и легко вычисляемы. Обоснование возможности представлять функцию многочленом дает формула Тейлора.
24. Неявно заданная функция
Если функция задана уравнением у=ƒ (х), разрешенным относительно у, то функция задана в явном виде (явная функция).
Под неявным заданием функции понимают задание функции в виде уравнения F(x; y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ (х)-у=0, но не наоборот.
Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2у-х+у=0).
Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'.
Производная неявной функции выражается через аргумент х и функцию у.
45. Функции нескольких переменных: основные понятия, предел и непрерывность
Опр. Если каждой паре значений переменных хи у из множества Д по закону f соответствует одно значение переменной z из множества Е, то переменная z назыв. Функцией от 2-х переменных ху. Z=f(x: y)
Д-область определения ф-ии и представляет из себя множество точек плоскости. Е-область значений ф-ии и явл числовым промежутком
Опр. Окрестностью точки Мо(хо; уо) назыв. круг с центром в этой точке причем радиус круга назыв. Радиусом окрестности.
Опр. Точка назыв. Внутренней точкой области, если найдется такая окрестность этой точки, которая лежит в этой области.
Опр.: точка назыв граничной точкой области если в любой её окрестности есть точки принадлежащие не принадлежащие этой области.
Опр: Область назыв замкнутой, если она состоит из внутренних и граничных точек.
Опр: область назв. Открытой, если граница не принадлежит этой области.
Опр: Графиком ф-ии 2-х переменных явл. Поверхность в пространстве уравнением которой будут уравнения этой фун-ии.
Опр: число в называется пределом функции двух переменных при М→  , если их разность является БМВ, обозначается: в=
, если их разность является БМВ, обозначается: в=  ↔ /в-f(x; y)/ → 0(БМВ), ели /в-f(x; y)/ → α, альфа БМВ. Если М→
↔ /в-f(x; y)/ → 0(БМВ), ели /в-f(x; y)/ → α, альфа БМВ. Если М→  , х→
, х→  , y→
, y→  , то
, то  - Двойной предел. Замечание: для двойного предела, справедливы те же свойства пределов, так же как и для функции одной переменной. Вычисление двойного предела:
- Двойной предел. Замечание: для двойного предела, справедливы те же свойства пределов, так же как и для функции одной переменной. Вычисление двойного предела: 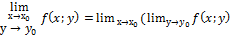 ) Опред: функция двух переменных называется непрерывной в точке
) Опред: функция двух переменных называется непрерывной в точке  если функция существует в этой точке и значение пределов в этой точке равно значению функции в этой же точке.
если функция существует в этой точке и значение пределов в этой точке равно значению функции в этой же точке.
44. Несобственные интегралы: интеграл по бесконечному промежутку, интеграл от неограниченной функции. Признаки сходимости несобственных интегралов
Ин интегралы с бесконечными пределами интегрирования или от разрывных функций называют несобственными.
1) несобственные интегралы с бесконечными пределами интегрирования
Определяются по средствам предельного перехода  =
=  (1)
(1)
 =
=  (2)
(2)
 =
=  , где c-произвольное действительное число
, где c-произвольное действительное число
2) несобственные интегралы от функции с бесконечными разрывами
Также определяется по средствам предельного перехода.
Если функция y=f(x) имеет бесконечный разрыв в точке c [x=c ∈ [a, b]) и непрерывна во всех других точках этого отрезка, то
 =
= 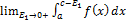 +
+ 
Несобственные интегралы называют сходящимися или расходящимися в зависимости от того существует или нет определение их пределы соответствующих определённых интегралов.
Признаки сходимости несобственных интегралов
В некоторых случаях нет необходимости вычислять несобственный интеграл, а достаточно лишь знать, сходится он или расходится. В таких случаях часто бывает полезным сравнить данный несобственный интеграл с другим несобственным интегралом, сходимость или расходимость которого известна. Приведём без доказательства теоремы, устанавливающие признаки сходимости или расходимости, основанные на сравнении несобственных интегралов.
Теорема 1: Пусть в интервале [a, +  ) функции f(x) и
) функции f(x) и 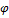 (x) непрерывны и удовлетворяют неравенствам 0≤
(x) непрерывны и удовлетворяют неравенствам 0≤ 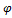 (x)≤ f(x). Тогда:
(x)≤ f(x). Тогда:
а) если интеграл 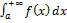 сходится, то сходится и интеграл
сходится, то сходится и интеграл 
б) если интеграл  расходится, то интеграл
расходится, то интеграл 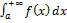 также расходится.
также расходится.
Теорема 2: Пусть функции f(x) и 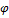 (x) в интервале [a, b) непрерывны и удовлетворяют неравенствам 0≤
(x) в интервале [a, b) непрерывны и удовлетворяют неравенствам 0≤ 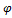 (x)≤ f(x), а в точке x=b имеют разрыв. Тогда:
(x)≤ f(x), а в точке x=b имеют разрыв. Тогда:
а) если интеграл  сходится, то сходится и интеграл
сходится, то сходится и интеграл 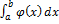
б) если интеграл 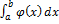 расходится, то интеграл
расходится, то интеграл  также расходится.
также расходится.
3-4. Если задана функция  , которая определена на множестве
, которая определена на множестве  и принимает значения в множестве
и принимает значения в множестве  , то есть, функция
, то есть, функция  отображает множество
отображает множество  в
в  , то
, то
- этот факт коротко записывают в виде
 или
или 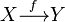 .
. - область определения функции
 (множество
(множество  ) обозначается
) обозначается 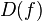 , или
, или  ;
; - область значений функции
 (множество
(множество  ) обозначается
) обозначается  (
( ), или
), или  (
(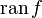 ).
). - Наличие функциональной зависимости между элементом
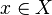 и элементом
и элементом  наиболее часто обозначается как
наиболее часто обозначается как
 ,
,
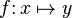 или
или
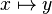 ;
;
- реже используется обозначение без скобок
 ,
,  или
или  ,
, - а там, где необходимо подчеркнуть двойственность, используются обозначения со скобками:
 или
или  ;
; - также существует и операторное обозначение
 , которое можно встретить в общей алгебре.
, которое можно встретить в общей алгебре. -
 в лямбда-исчислении Чёрча.
в лямбда-исчислении Чёрча.
· Функции нескольких аргументов
·
· 
· График функции двух переменных: 
· Определение функции легко обобщить на случай функции многих аргументов.
· Если множество  представляет собой декартово произведение множеств
представляет собой декартово произведение множеств 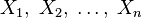 , тогда отображение
, тогда отображение  оказывается
оказывается  -местным отображением, при этом элементы упорядоченного набора
-местным отображением, при этом элементы упорядоченного набора  называются аргументами (данной
называются аргументами (данной  -местной функции), каждый из которых пробегает своё множество:
-местной функции), каждый из которых пробегает своё множество:
· 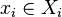 где
где 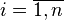 .
.
· В этом случае  означает, что
означает, что 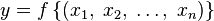 .
.
· Способы задания функции
· Аналитический способ[
· Функция как математический объект представляет собой бинарное отношение, удовлетворяющее определенным условиям. Функцию можно задать непосредственно как множество упорядоченных пар, например:  есть функция
есть функция  . Однако, этот способ совершенно непригоден для функций на бесконечных множествах (каковыми являются привычные вещественные функции: степенная, линейная, показательная, логарифмическая и т. п.).
. Однако, этот способ совершенно непригоден для функций на бесконечных множествах (каковыми являются привычные вещественные функции: степенная, линейная, показательная, логарифмическая и т. п.).
· Для задания функции пользуются выражением:  . При этом,
. При этом,  есть переменная, пробегающая область определения функции, а
есть переменная, пробегающая область определения функции, а  — область значений. Эта запись говорит о наличии функциональной зависимости между элементами множеств. х и y могут пробегать любые множества объектов любой природы. Это могут быть числа, векторы, матрицы, яблоки, цвета радуги. Поясним на примере:
— область значений. Эта запись говорит о наличии функциональной зависимости между элементами множеств. х и y могут пробегать любые множества объектов любой природы. Это могут быть числа, векторы, матрицы, яблоки, цвета радуги. Поясним на примере:
· Пусть имеется множество  яблоко, самолет, груша, стул
яблоко, самолет, груша, стул  и множество
и множество  человек, паровоз, квадрат
человек, паровоз, квадрат  . Зададим функцию f следующим образом:
. Зададим функцию f следующим образом:  (яблоко, человек), (самолет, паровоз), (груша, квадрат), (стул, человек)
(яблоко, человек), (самолет, паровоз), (груша, квадрат), (стул, человек)  . Если ввести переменную x, пробегающую множество
. Если ввести переменную x, пробегающую множество  и переменную y, пробегающую множество
и переменную y, пробегающую множество  , указанную функцию можно задать аналитически, как:
, указанную функцию можно задать аналитически, как:  .
.
· Аналогично можно задавать числовые функции. Например:  , где х пробегает множество вещественных чисел, задает некоторую функцию f. Важно понимать, что само выражение
, где х пробегает множество вещественных чисел, задает некоторую функцию f. Важно понимать, что само выражение  не является функцией. Функция, как объект, представляет собой множество (упорядоченных пар). А данное выражение, как объект, есть равенство двух переменных. Оно задает функцию, но не является ею.
не является функцией. Функция, как объект, представляет собой множество (упорядоченных пар). А данное выражение, как объект, есть равенство двух переменных. Оно задает функцию, но не является ею.
· Однако, во многих разделах математики, можно обозначать через f(x) как саму функцию, так и аналитическое выражение, ее задающее. Это синтаксическое соглашение является крайне удобным и оправданным.
· Графический способов
· Числовые функции можно также задавать с помощью графика. Пусть  — вещественная функция n переменных.
— вещественная функция n переменных.
· Рассмотрим некоторое (n+1)-мерное линейное пространство над полем вещественных чисел (так как функция вещественная). Выберем в этом пространстве любой базис (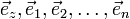 ). Каждой точке функции сопоставим вектор:
). Каждой точке функции сопоставим вектор:  . Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
. Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
· Если в качестве линейного пространства взять евклидово пространство свободных геометрических векторов (направленных отрезков), а число аргументов функции f не превосходит 2, указанное множество точек можно изобразить наглядно в виде чертежа (графика). Если сверх того исходный базис взять ортонормированным, получим «школьное» определение графика функции.
· Для функций 3 аргументов и более такое представление не применимо ввиду отсутствия у человека геометрической интуиции многомерных пространств.
· Однако, и для таких функций можно придумать наглядное полугеометрическое представление (например каждому значению четвертой координаты точки сопоставить некоторый цвет на графике).
Числовая последовательность — это последовательность элементов числового пространства. Пусть — это либо множество вещественных чисел, либо множество комплексных чисел. Тогда последовательность элементов множества называется числовой последовательностью
Суммой числовых последовательностей  и
и  называется числовая последовательность
называется числовая последовательность  такая, что
такая, что 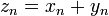 .
.
Разностью числовых последовательностей  и
и  называется числовая последовательность
называется числовая последовательность  такая, что
такая, что  .
.
Произведением числовых последовательностей  и
и  называется числовая последовательность
называется числовая последовательность  такая, что
такая, что  .
.
Частным числовой последовательности  и числовой последовательности
и числовой последовательности  , все элементы которой отличны от нуля, называется числовая последовательность
, все элементы которой отличны от нуля, называется числовая последовательность 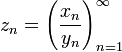 . Если в последовательности
. Если в последовательности  на позиции
на позиции 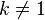 всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность
всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность  .
.
Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.
Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.
Верхний предел последовательности — это наибольшая предельная точка этой последовательности.
Нижний предел последовательности — это наименьшая предельная точка этой последовательности.
Свойства ограниченных последовательностей[править | править исходный текст]
- Ограниченная сверху числовая последовательность имеет бесконечно много верхних граней.
- Ограниченная снизу числовая последовательность имеет бесконечно много нижних граней.
- Ограниченная последовательность имеет по крайней мере одну предельную точку.
- У ограниченной последовательности существуют верхний и нижний пределы.
- Для любого наперёд взятого положительного числа
 все элементы ограниченной числовой последовательности
все элементы ограниченной числовой последовательности 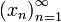 , начиная с некоторого номера, зависящего от
, начиная с некоторого номера, зависящего от  , лежат внутри интервала
, лежат внутри интервала  .
. - Если за пределами интервала
 лежит лишь конечное число элементов ограниченной числовой последовательности
лежит лишь конечное число элементов ограниченной числовой последовательности 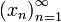 , то интервал
, то интервал  содержится в интервале
содержится в интервале  .
. - Справедлива теорема Больцано — Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.