Теорема.

Если ряд сходится, то его общий член стремится к нулю, т.е. .

Док-во. Пусть ряд сходится и . Тогда и . Учитывая, что при n> 1, получаем:

.

Следствие (достаточное условие расходимости ряда)

Если или этот предел не существует, то ряд расходится.

Действительно, если бы ряд сходился, то (по теореме) 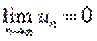. Но это противоречит условию. Значит, ряд расходится.

Теорема о сходимости дает необходимое условие сходимости ряда, но не достаточное: из условия не следует, что ряд сходится. Это означает, что существуют расходящиеся ряды, для которых .

В качестве примера рассмотрим так называемый гармонический ряд

Очевидно, что 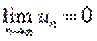. Однако ряд расходится.

Пример 3. Проверить выполнение необходимого признака сходимости:

а) ;

б) .

Р е ш е н и е.

а)

Вычислим 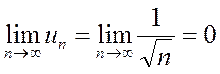, т.е. необходимый признак сходимости ряда выполняется. С другой стороны, оценим его n -ую частичную сумму

Таким образом, . Но при n ® ¥ , а, следовательно, и , т.е. ряд расходится (несмотря на то, что предел общего члена ряда равен нулю).

б)

Так как Þ ряд расходится. ¨

Т2.Еслиряд сходится, то

Здесь —это так называемый n -ый остаток ряда.

Доказательство: Если то а поскольку при то при

Теорема 3. Если ряды и сходятся и их суммы равны соответственно и 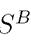, то для любых чисел ряд сходится и его сумма выражается формулой

Доказательство: Для любого имеем:

Первое слагаемое стремится к , а второе —к при Таким образом, предельный переход при дает что и требовалось доказать.

Теорема 4. Если у сходящегося ряда отбросить конечное число первых членов ряда, то полученный ряд также будет сходиться.

Д о к а з а т е л ь с т в о.

Пусть дан сходящийся ряд u₁+u₂+…+u_n+…. Выбросим из него конечное число членов (например, , на их место поставим нули). Тогда при n> 15 частичные суммы обоих рядов отличаются на постоянное слагаемое . И если существует предел частной суммы одного ряда , то существует частная сумма второго ряда 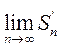, т.к. . Тогда = = = .

Аналогично рассуждаем в общем случае.Обозначим через —

сумму n первых членов ряда , 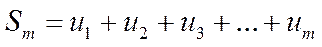— сумму m отброшенных членов (m< n), — сумму n—m первых членов полученного остатка ряда после m -го члена: .

Тогда .Если ряд сходится, то существует .Тогда ,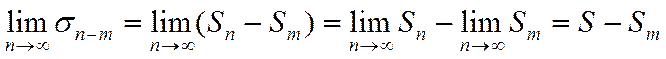

т.е. последовательность частичных сумм σ _n-m ряда имеет конечный предел. Следовательно, ряд сходится.