
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи на основные законы распределения
|
|
Задача 1. По каналу связи передаются пять сообщений. Каждое сообщение, независимо от других может быть искажено с вероятностью 0, 3. Составить ряд распределения числа искажений. Найти среднее значение числа искажений, среднее квадратическое отклонение от среднего значения. Найти вероятность того, что искажений будет не менее двух.
Решение. X - число искаженных сообщений. Их может быть: 0, 1, 2, 3, 4, 5. Т.к. испытания независимые, то вероятность с которыми эти значения принимаются можно подсчитать по формуле Бернулли:
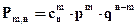
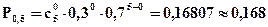
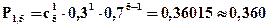
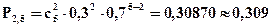

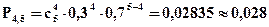
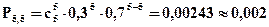
Ряд распределения имеет вид:
| xi | ||||||
| pi | 0, 168 | 0, 360 | 0, 309 | 0, 133 | 0, 028 | 0, 002 |
Проверим, что  Действительно:
Действительно:
0, 168 + 0, 360 + 0, 309 + 0, 133 + 0, 028 + 0, 002 = 1
Найдем числовые характеристики.
Так как распределение биномиальное, то М(х) =nр, т.е.
М(х) = 5·0, 3 = 1, 5
Убедитесь самостоятельно, что этот же результат можно получить вычисляя М(х) по формуле: 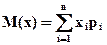
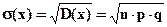
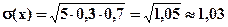
Найдем Р(Х≥ 2),
P(x≥ 2)=P2, 5+P3, 5+P4, 5+P5, 5=0, 309+0, 133+0, 028+0, 002=0, 472
или более рационально Р(Х≥ 2)=1-Р(Х< 2)=1-[Р0, 5+P1, 5]=
=1-[0, 168+0, 360]≈ 0, 472
Задача 2. Поток грузовых железнодорожных составов, прибывающих на станцию, можно считать простейшим с интенсивностью четыре состава в один час. Найти среднее число составов, прибудущих на станцию в течение получаса. Найти вероятность того, что в течении получаса на станцию прибудет: а) ровно один состав; б) хотя бы один состав.
Решение. Х- число составов прибывающих на станцию (0, 1, 2,..., m,...) т.к. имеет место простейший поток событий то для подсчета можно применить формулу Пуассона 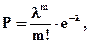 где
где 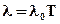
Известно, что λ 0 = 4; Т=0, 5; тогда λ =λ 0 Т=4·0, 5 = 2.
Для распределения Пуассона М(х)=λ =2 - среднее число составов, которое может прибыть в течение получаса.
Найдем: 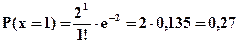
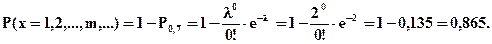
Задача 3. Случайная величина X - число лампочек исправных, которое выбирается из десяти. Каждая лампочка с вероятностью 0, 6 может иметь дефект. Построить ряд распределений. Найти среднее число исправных лампочек.
Решение: Х+1: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Лампочки выбираются до первой исправной, т.е. имеет место геометрическое распределение, сдвинутое на единицу, т.е. pm = qm-1 p, тогдаряд распределения имеет вид:
| xi | ||||||||||
| pi | 0, 4 | 0, 6·0, 4 | 0, 62·0, 4 | 0, 63·0, 4 | 0, 64·0, 4 | 0, 65·0, 4 | 0, 66·0, 4 | 0, 67·0, 4 | 0, 68·0, 4 | 0, 69·0, 4 |
А математическое ожидание: 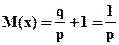
По условию задачи q = 0, 6; р = 0, 4, тогда 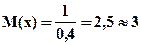
Задача 4. В шкафу находится 9 приборов; из них 5 исправных. Из шкафа наугад берется 4 прибора. Вычислить математическое ожидание числа исправных приборов и построить ряд распределения.
Решение: X - число исправных приборов: оно может изменяться от 0 до 4.
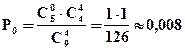
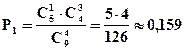

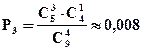
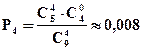
Ряд распределения имеет вид:
| xi | |||||
| pi | 0, 008 | 0, 159 | 0, 476 | 0, 317 | 0, 040 |
Найдем 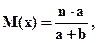 как математическое ожидание гипергеометрического распределения:
как математическое ожидание гипергеометрического распределения: 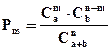
В данном случае 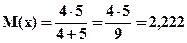
РАЗДЕЛ II. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение случайной величины.
2. Что понимать под законом распределения случайной величины?
Каково его основное свойство? Что называется рядом распределения?
3. Дайте определение интегральной функции распределения F(x).
Сформулируйте ее свойства.
4. Дайте определение дифференциальной функции распределения f(x). Сформулируйте ее свойства.
5. Как найти для непрерывной случайной величины:
а) дифференциальную функцию распределения при известной
интегральной;
в) интегральную функцию распределения при известной дифференциальной?
6. Дайте определение математического ожидания М(Х) случайной величины. Сформулируйте его свойства. Запишите формулы для вычисления М(Х) дискретной и непрерывной случайных величин.
7. Дайте определение дисперсии D(X) случайной величины. Сформулируйте ее свойства. Запишите формулы для вычисления D(X) дискретной и непрерывной случайных величин.
8. Дайте определение среднего квадратического отклонения и укажите его преимущества по сравнению с дисперсией.
9. Дайте определение начальных и центральных моментов " к" -го порядка.
10. Запишите законы распределения дискретных случайных величин: а) биномиального;
в) пуассоновского;
и формулы для вычисления их числовых характеристик.
11. Запишите формулы Бернулли и Пуассона. Когда они применяются и какая между ними существует связь?
12. Дайте определение законов распределения непрерывных случайных величин:
а) равномерного;
6) показательного;
в) нормального.
Запишите формулы для вычисления их числовых характеристик. Нарисуйте графики f(x).
13. Сформулируйте локальную и интегральную теоремы Лапласа.
14. Как найти вероятность попаданий случайной величины на заданный интервал, если она распределена по закону:
а) показательному;
б) нормальному?
15. Сформулируйте теорему Ляпунова.
16. Запишите неравенство Чебышева.
17. Сформулируйте теорему Чебышева.
Запишите формулу для оценки вероятности того, что среднее арифметическое попарно независимых случайных величин, дисперсии которых равномерно ограничены, отклонится от среднего арифметического их математических ожиданий по абсолютной величине меньше, чем на ε.
18. Сформулируйте теорему Бернулли. Запишите формулу для оценки вероятности того, что относительная частота появления события А в n независимых испытаниях отклонится от вероятности р по абсолютной величине меньше, чем на ε,
Замечание: В пунктах 17 и 18 ε - как угодно малое положительное число.
РАЗДЕЛ III. РЕШЕНИЕ ПРИМЕРНОГО ВАРИАНТА ИНДИВИДУАЛЬНОГО ЗАДАНИЯ
Задача №1. Непрерывная случайная величина X задана дифференциальной функцией;
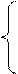
|
Ах2; если 0≤ x< 2
0; если х≥ 2
Найти: а) коэффициент А;
б) интегральную функцию F(x);
в)математическое ожидание, дисперсию, среднее квадратическое отклонение;
г) Р(0 ≤ X ≤ 1)
построить графики F(x) и f(x).
Задачу № 2 Прибор состоит из трех узлов. Каждый из узлов может выйти из строя за время Т независимо от других с вероятностью 0, 1.
Составить: а) ряд распределения;
б) функцию распределения числа узлов прибора,
вышедших из строя за время Т.
Построить: многоугольник распределения и график функции
распределения.
Найти: в) математическое ожидание, дисперсию, среднее квадратическое отклонение рассматриваемой случайной величины;
г) вероятность того, что за время Т выйдет из строя не более двух узлов.
Задача №3 На склад поступают крепежные болты, среди которых 10% бракованных. Какова вероятность того, что среди случайно отобранной партии из 100 болтов, годных будет не менее 80?
Задача № 4 Среднее число вызовов, поступающих на АТС за 1 минуту равно 2. Найти вероятность того, что за 3 минуты поступит хотя бы один вызов, если число вызовов распределено по закону Пуассона.
Задача № 5. Найти вероятность попадания в интервал (4; 8) нормально распределенной случайной величины X, если известны ее математическое ожидание а=7 и среднее квадратическое отклонение σ =2.
Задача № 6. Одна из установок содержит 10 однотипных деталей, каждая из которых может выйти из строя за определенное время Т независимо от остальных с вероятностью 0, 1. Оценить снизу вероятность того, что число деталей, вышедших из строя за время Т, отличается от своего математического ожидания меньше, чем на 3.
Задача № 7. Вычислить двумя способами М(Х2Y+3), если заданы распределения двух независимых случайных величин:
| x | -1 | y | |||||
| p | 0, 2 | 0, 5 | 0, 3 | q | 0, 6 | 0, 4 |
Выполнение варианта №0
 Задача №1. Непрерывная случайная величина Х задана дифференциальной функцией:
Задача №1. Непрерывная случайная величина Х задана дифференциальной функцией:
|
Ах2; если 0≤ x< 2
0; если х≥ 2
Найти: а) коэффициент А;
б) интегральную функцию F(x);
в) математическое ожидание, дисперсию, среднее квадратиче-
ское отклонение;
г) Р(0< Х< 1)
построить графики F(x) и f(x).
Решение: а) для нахождения коэффициента А воспользуемся свойст- вом дифференциальной функции
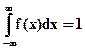
 при
при 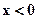 и x> 2, то
и x> 2, то 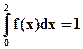
Отсюда 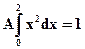 итак,
итак,
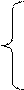 0; при х< 0
0; при х< 0
|
0; при х≥ 2
б) при известной f(x),
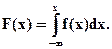
Если дифференциальная функция f(x) задана тремя различными формулами и при х< а и х> b f(x)=0, то интегральная функция распределения будет иметь вид:
 0; при х< a
0; при х< a
|
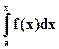 ; при a≤ x< b
; при a≤ x< b
1; при х≥ b
В нашем случае
 0; при х< 0
0; при х< 0
|
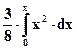 ; при 0≤ x< 2
; при 0≤ x< 2
1; при х≥ 2
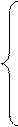 или
или
0; при х< 0
|
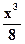 ; при 0≤ x< 2
; при 0≤ x< 2
1; при х≥ 2
в) математическое ожидание непрерывной случайной величины находится по формуле: 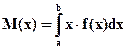 Имеем
Имеем 
Дисперсию можно найти по одной из формул:
D(x) = М(х2) - М2(х) или D(x) = М(х-М(х))2
Воспользуемся первой формулой, для чего вычислим 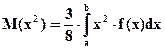
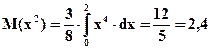
Получим D(X) = 2, 4 - 2, 25 = 0, 15
Среднее квадратическое отклонение: 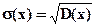

г) Если известна интегральная функция распределения для непрерывной случайной величины, то Р(α < X < β) = F(β) - F(α)
Заметим, что [0; 1] целиком входит в отрезок [0; 2], на котором
 поэтому
поэтому 
Графики функций F(x) и f(x) будут иметь следующий вид:
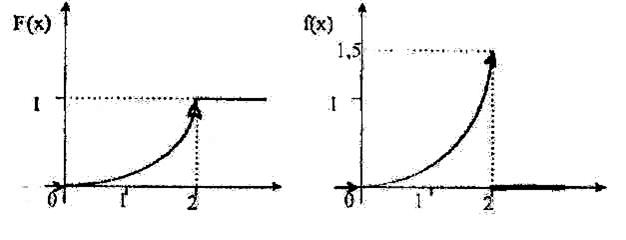
Задача № 2 Прибор состоит из трех узлов. Каждый из узлов может выйти из строя за время Т независимо от других с вероятностью 0, 1.
Составить: а) ряд распределения;
б) функцию распределения числа узлов прибора, вышедших
из строя за время Т.
Построить многоугольник распределения и график функции
распределения.
Найти: в) математическое ожидание, дисперсию, среднее квадрати-
ческое отклонение рассматриваемой случайной величины;
г) вероятность того, что за время Т выйдет из строя не
более двух узлов.
Решение:
Рекомендация. Решение большинства задач на тему " Случайные величины" нужно начинать с определения того, что является в задаче случайной величиной.
При решении данной задачи ставим вопрос: " Построить ряд распределения, функцию распределения чего? "; отвечаем: " Числа узлов прибора, вышедших из строя за время Т ".
Следовательно, случайная величина X - число узлов прибора, вышедших из строя за время Т.
а) Составим закон (ряд) распределения рассматриваемой случайной величины. Прибор состоит из трех узлов, поэтому за время Т могут выйти из строя 0, 1, 2 или все 3 узла.
Итак, X принимает значения х=0; х=1; х=2; х=3. Найдем соответствующие вероятности. Так как каждый из узлов может выйти из строя за время Т независимо один от другого с одной и той же вероятностью 0, 1, то вероятность того, что из трех узлов X = m выйдет из строя будет вычисляться по формуле Бернулли:
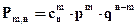
В нашем случае p = 0, 1; q = 1-0, 1 =0, 9.
Тогда
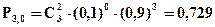

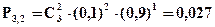
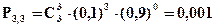

Замечание. Так как события X1=0; Х2=1; Х3=2 составляют полную группу, то 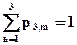
Многоугольник распределения данной случайной величины имеет вид:
б) По определению функция распределения F(X) = Р(Х < х),
где 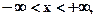
следовательно при x< 0 F(x) = 0
0≤ x< 1 F(x) = Р3, 0 = 0, 729
1≤ x< 2 F(x)=P3, 0+P3, 1=0, 972
2≤ x< 3 F(x)= P3, 0+P3, 1+P3, 2=0, 999
3≤ x< 4 F(x)= P3, 0+P3, 1+P3, 2+P3, 3=1
Итак
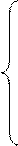 |
0 при х< 0
|
0, 972 при 0 ≤ х < 2
0, 999 при 0 ≤ х< 3
1 при х ≥ 3
График функции будет иметь вид:

в) математическое ожидание дискретной случайной величины вычисляется по формуле: 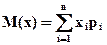 В нашей задаче:
В нашей задаче:
М(Х) = 0·0, 729 +1·0, 243 + 2·0, 027 + 3·0, 001 = 0, 3
Найдем дисперсию: D(x) = М(х2) – М2(х)
Для вычисления М(х2) составим закон распределения случайной величины X, для чего найденные значения случайной величины необходимо возвести в квадрат, оставив соответствующие вероятности без изменений, т.е.
| xi | ||||
| pi | 0, 729 | 0, 243 | 0, 027 | 0, 001 |
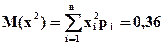 D(x) = 0, 36 - 0, 09 = 0, 27
D(x) = 0, 36 - 0, 09 = 0, 27
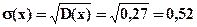
г) Для нахождения искомой вероятности следует ответить на вопрос: " Сколько узлов может выйти из строя за время Т? ";
ответ: " За время Т выйдет из строя 0, или 1, или 2 узла, т.е.
Р(Х≤ 2)=Р3, 0 + Р3, 1 + Р3, 2 = 0, 999
Эту же вероятность удобнее найти используя формулу:
Р(Х≤ 2) = 1 - Р3, 3 = 1 - 0, 001 = 0, 999
Задача № 3. На склад поступают крепежные болты, среди которых 10% бракованных. Какова вероятность того, что среди случайно отобранной партии из 100 болтов, годных будет не менее 80?
Решение. Для ответа на вопрос задачи необходимо воспользоваться интегральной теоремой Лапласа.
Р(а < X < b) = Ф(х2) - Ф(x1), где 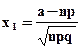

Имеем n=100; р=1-0, 1=0, 9; q=0, 1; nр=90
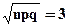
По условию задачи нужно найти Р(80< X< 100), поэтому
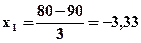
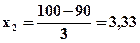
Р(80< X< 100)=Ф(3, 33)- Ф(-3, 33) =2Ф(3, 33)=2·0, 4995=0, 999
Замечание. Значения функции Ф(х) находятся по таблице 2 приложения
Задача № 4 Среднее число вызовов, поступающих на АТС за 1 минуту равно 2. Найти вероятность того, что за 3 минуты поступит хотя бы один вызов, если число вызовов распределено по закону Пуассона.
Решение. В задаче необходимо найти вероятность того, что за 3 минуты на АТС поступит хотя бы один вызов. Это значит: один или более.
Р будет находиться по формуле Пуассона:
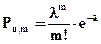
В нашем случае λ - среднее число вызовов, которое поступит на АТС за 3 минуты. Так как за 1 минуту, в среднем, поступает 2 вызова, то за 3 минуты поступит λ =2·3=6 вызовов.
Тогда 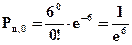
Поэтому вероятность того, что за 3 минуты поступит хотя бы один вызов будет равна:
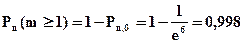
Задача №5. Найти вероятность попадания в интервал (4; 8) нормально распределенной случайной величины X, если известны ее математическое ожидание а=7 и среднее квадратическое отклонение σ =2.
Решение. Вероятность попадания в интервал (α; β) нормально распределенной случайной величины вычисляется по формуле:
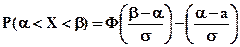
В данной задаче
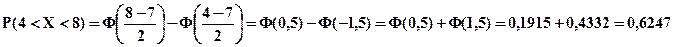 Замечание. Значения функции Ф(х) находятся по таблице 2 приложения.
Замечание. Значения функции Ф(х) находятся по таблице 2 приложения.
Задача № 6. О дна из установок содержит 10 однотипных деталей, каждая из которых может выйти из строя за определенное время Т независимо от остальных с вероятностью 0, 1. Оценить снизу вероятность того, что число деталей, вышедших из строя за время Т, отличается от своего математического ожидания меньше, чем на 3.
Решение. По условию задачи необходимо оценить Р(|Х-M(X)|< 3)
Для этого используем неравенство Чебышева 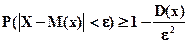
Найдем D(X). Т.к. рассматриваемая случайная величина подчиняется
биномиальному распределению, то D(X) = npq, где n=10; р=0, 1; q=0, 9.
Отсюда 
Задача 7. Вычислить двумя способами М(Х2Y+3), если заданы распределения двух независимых случайных величин:
| X x | -1 -1 | 0 0 | 1 1 | Y Y | 1 1 | 2 2 | |
| р p | 0, 2 0, 2 | 0, 5 0, 5 | 0, 3, 0, 3i | Ц q | 0, 6 0, 6 | 0, 4 0, 4 |
Решение. М(Х2У + 3) можно вычислить, пользуясь изученными свойствами математического ожидания, и непосредственно по определению, составив предварительно закон распределения случайной величины (X2У+3).
При решении данной задачи, в обоих случаях, нам необходим закон распределения случайной величины X2. Составим его:
| X2 | -1 | ||
| p | 0, 2 | 0, 5 | 0, 3 |
Так как в нашем случае X2 дважды принимает значение равное 1, то этот же закон распределения можно записать иначе:
| X2 | ||
| p | 0, 5 | 0, 5 |
Замечание. Написав значение X2=1 один раз, соответствующие вероятности р=0, 2 и р=0, 3 необходимо сложить.
| X2 | Y | |||||
| p | 0, 5 | 0, 5 | q | 0, 6 | 0, 4 |
Составим закон распределения случайной величины (X2·Y + 3) Чтобы получить значения рассматриваемой случайной величины, нужно найти все возможные произведения X2·Y, а затем прибавить к каждому из них 3, т.е.
0, 1+3; 1, 1+3; 1, 2 + 3; 0.2
Тогда X2Y + 3 будет принимать значения: 3; 3; 4; 5.
Соответствующие вероятности следует перемножить:
0, 5·0, 6; 0, 5·0, 4; 0, 5·0, 6; 0, 5·0, 4.
В результате получаем:
| X2Y + 3 | ||||
| P | 0, 3 | 0, 2 | 0, 3 | 0, 2 |
или
| X2Y + 3 | |||
| P | 0.5 | 0.3 | 0.2 |
По определению M(X2 ·Y+3)=3·0, 5+4·0, 3+5·0, 2=3, 7
Найдем M(х2 ·Y+3), пользуясь свойствами математического ожидания.
M(X2 ·Y+3)=M(x2)·M(Y)+3
Вычислим М(Х2) = 0, 5; M(Y) = 1, 4
Тогда M(X2 ·Y+3)= 0, 5·1, 4 + 3 = 3, 7
Ответ: M(X2 ·Y+3)= 3, 7
РАЗДЕЛ IV. ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
Вариант 1.
1.Непрерывная случайная величина задана интегральной функцией:
|
 0; при х< 0
0; при х< 0
Ах2; при 0≤ x< 10
0; при х≥ 10
Найти: а) коэффициент А;
б) дифференциальную функцию f(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) Р(0≤ X≤ 5);
д) построить графики f(x) и F(x).
2. Производится 3 независимых выстрела с вероятностью попадания 0, 6 при каждом выстреле.
Составить: а) ряд распределения, возникающей при этом случайной
величины;
б) функцию распределения. Найти:
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) вероятность хотя бы одного промаха;
д) построить многоугольник распределения и
график функции распределения.
3. Вероятность появления события в каждом из независимых испытаний равна 0, 8. Найти вероятность того, что в 100 испытаниях событие появится не менее 70 и не более 80 раз.
4. Среднее число самолетов, прибывающих в аэропорт за 1 минуту равно двум. Найти вероятность того, что за 3 минуты прибудут два самолета. (Считать, что число прибывающих самолетов распределено по закону Пуассона).
5. Найти вероятность попадания в интервал (2; 13) нормально распределенной случайной величины X, если известны ее математическое ожидание а=10 и среднее квадратическое отклонение σ = 4.
6. Монету подбрасывают 1000 раз. Оценить вероятность того, что частота появления герба отклонится от вероятности его появления меньше, чем на 0, 1.
7. Вычислить двумя способами М(Х2-Y), если заданы законы распределения независимых случайных величин:
| x | Y | -1 | |||||
| p | 0, 4 | 0, 6 | q | 0, 3 | 0, 5 | 0, 2 |
Вариант 2
1. Непрерывная случайная величина X задана интегральной функцией:
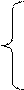 0; при х< 0
0; при х< 0
|
0; при х≥ 9
Найти: а) коэффициент А;
б) дифференциальную функцию f(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) Р(0≤ X≤ 5);
д) построить графики F(x) и f(x).
2. Производится 5 независимых выстрелов по мишени, вероятность попадания в которую при каждом выстреле равна 0, 2.
Составить: а) ряд распределения, возникающей при этом
случайной величины;
б) функцию распределения;
Найти: в) математическое ожидание, дисперсию и среднее
квадратическое отклонение;
г) вероятность не менее 3 попаданий в мишень;
д) построить многоугольник распределения и график
функции распределения.
3.Вероятность появления события в каждом из независимых испытаний равна 0, 2. Найти вероятность того, что при 100 испытаниях событие наступит 20 раз.
4. Среднее число самолетов, прибывающих за 1 минуту равно 2. Найти вероятность того, что за 3 минуты прибудет менее двух самолетов (считать, что число прибывающих самолетов распределено по закону Пуассона).
5. Найти вероятность попадания в интервал (5; 14) нормально распределенной случайной величины X, если известны ее математическое ожидание а=9 и среднее квадратическое отклонение σ =5.
6. В урне 1000 белых и 2000 черных шаров. Вынули (с возвращением) 300 шаров. Оценить снизу вероятность того, что число извлеченных при этом шаров удовлетворяет неравенству 80< m< 120.
7. Вычислить двумя способами М(2Х+3Y), если заданы законы распределения независимых случайных величин:
| X | Y | ||||||
| p | 0, 3 | 0, 7 | q | 0, 1 | 0, 3 | 0, 6 |
Вариант 3
1. Непрерывная случайная величина задана дифференциальной функцией:
|
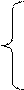 0; при х< 0
0; при х< 0
Ах2; при 0≤ x< 1
1; при х≥ 1
Найти: а) коэффициент А;
б) интегральную функцию F(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) Р(0≤ X≤ 0, 5);
д) построить графики F(x) и f(x).
2. Производится 3 выстрела по мишени. Вероятности попадания при первом, втором и третьем выстрелах соответственно равны: р=0, 4; р=0, 5; Р=0, 7.
Составить: а) ряд распределения, возникающей при этом
случайной величины;
б) функцию распределения;
в) построить многоугольник распределения и график
функции распределения.
Найти: г) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
д) вероятность хотя бы одного попадания в мишень.
3. Вероятность появления события в каждом из независимых испытаний равна 0, 3. Найти вероятность того, что событие наступит 120 раз в 144 испытаниях.
4. Книга в 1000 страниц имеет 100 опечаток. Какова вероятность того, что на случайно выбранной странице не менее двух опечаток, если число распределено по закону Пуассона.
5. Найти вероятность попадания в интервал (4; 9) нормально распределенной случайной величины X, если известны ее математическое ожидание а=8 и среднее квадратическое отклонение σ =1.
6. Урожайность пшеницы с 1 га на обследуемом участке является случайной величиной, математическое ожидание которой М(Х)=30ц, а дисперсия D(x)=16. Оценить вероятность того, что количество пшеницы, собранной с 1 га этого участка будет от 25ц до 35ц.
7. Вычислить двумя способами М(Х2+1), если задан закон распределения:
| x | |||
| p | 0, 2 | 0, 5 | 0, 3 |
Вариант 4.
1. Непрерывная случайная величина X задана дифференциальной функцией:
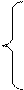 0; при х< 0
0; при х< 0
|
0; при х≥ 1
Найти: а) коэффициент а;
б) интегральную функцию F(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) Р(0, 8≤ X≤ 2);
д) построить графики F(x) и f(x)
2. В некотором цехе брак составляет 5% всех изделий.
Составить: а) ряд распределения;
б) функцию распределения числа бракованных изделий из
трех наудачу взятых;
в) построить многоугольник распределения и график
функции распределения.
Найти: г) математическое ожидание, дисперсию и среднее
квадратическое отклонение рассматриваемой случайной
величины;
д) вероятность того, что среди трех изделий будет не менее
двух бракованных.
3. В партии смешаны детали двух сортов: 80% - первого и 30% - второго. Сколько деталей первого сорта с вероятностью 0, 0967 можно ожидать среди 100 наудачу взятых деталей (выборка возвратная).
4. Вероятность попадания в цель при каждом выстреле равна 0, 0001. Найти вероятность не менее двух попаданий в цель при 5000 выстрелах.
5. Найти вероятность попадания в интервал (8; 10) нормально распределенной случайной величины X, если известны ее математическое ожидание а=7 и среднее квадратическое отклонение σ =2.
6. В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за время Т лампа будет включена, равна 0, 8. Оценить вероятность того, что число ламп, включенных в осветительную сеть за время Т, отличается от своего математического ожидания по абсолютной величине не более, чем на 3.
7. Вычислить двумя способами М(ЗХ+1), если
| x | -1 | ||
| p | 0, 1 | 0, 3 | 0, 6 |
Вариант 5.
1. Непрерывная случайная величина X задана интегральной функцией:
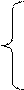 0; при х< 0
0; при х< 0
|
1; при х≥ 8
Найти: а) коэффициент А;
б) дифференциальную функцию f(x);.
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) Р(0≤ X≤ 4);
д) построить графики F(x) и f(x)
2. Производится два независимых выстрела с вероятностями попадания в цель p1=0, 6; р2=0, 5
Составить: а) ряд распределения;
б) функцию распределения числа попаданий в мишень;
в) построить многоугольник распределения и график
функции распределения.
Найти: г) математическое ожидание, дисперсию, среднее
квадратическое отклонение рассматриваемой случайной
величины;
д) вероятность поражения цели.
3. На склад магазина поступают изделия, из которых 80% оказываются высшего сорта. Найти вероятность того, что из 100 взятых наудачу изделий не менее 85 высшего сорта.
4. Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час, равно 3. Найти вероятности того, что за 2 часа поступит не менее 2-х заявок, если число заявок распределено по закону Пуассона.
5. Чему равна вероятность того, что нормальная случайная величина с математическим ожиданием равным 3 и дисперсией равной 1, примет значение из интервала (0, 5; 3, 5)?
6. Электростанция обслуживает сеть с 18000 ламп, вероятность включения каждой из которых в зимний вечер равна 0, 9. Оценить вероятность того, что число ламп, включенных в сеть зимним вечером, отличается от своего математического ожидания по абсолютной величине не более, чем на 100?
7. Вычислить двумя способами М(2+XY), если заданы законы распределения независимых случайных величин:
| x | Y | ||||||
| p | 0, 3 | 0, 7 | q | 0, 4 | 0, 3 | 0, 3 |
Вариант 6.
1. Непрерывная случайная величина X задана интегральной функцией:
|
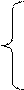 0; при х< -1
0; при х< -1
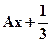 ; при -1≤ x< 2
; при -1≤ x< 2
0; при х≥ 2
Найти: а) коэффициент А;
б) дифференциальную функцию f(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) P(0≤ x≤ 4)
д) построить графики F(x) и f(x)
2. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется стандартной, равна 0, 9.
Составить: а) ряд распределения;
б) функцию распределения числа стандартных деталей
среди 4-х проверенных;
в) построить многоугольник распределения и график
функции распределения.
Найти: г) математическое ожидание, дисперсию, среднее
квадратическое отклонение рассматриваемой случайной
величины;
д) вероятность того, что среди этих 4-х проверенных
деталей бракованных будет не менее 3-х.
3. В процессе эксплуатации электронно-вычислительной машины М-20 установлено, что в течение года в среднем отказывает 60 ламп. Полагая, что число отказов ламп распределено по закону Пуассона. Найти вероятность, того, что в течение месяца откажет не более одной лампы.
4. Вероятность наступления события А в данном испытании равна 0, 7. Найти вероятность того, что это событие при 900 испытаниях произойдет 660 раз.
5. Изделия, выпускаемые цехом, по своим линейным размерам распределяются по нормальному закону с математическим ожиданием а=6см и средним квадратическим отклонением σ =0, 02см. Какова вероятность того, что наудачу взятое одно изделие будет иметь размеры в пределах от 5, 95 до 6, 05 см?
6. Вероятность наступления некоторого события в каждом испытании равна 0, 4. Оценить вероятность того, что отклонение частости от вероятности наступления события в отдельном испытании не превысит 0, 01 при 12000 испытаниях.
7. Вычислить двумя способами математическое ожидание и дисперсию случайной величины ЗХ-2, если задан закон распределения:
| x | -1 | ||
| p | 0, 2 | 0, 3 | 0, 5 |
Вариант 7.
1.  Непрерывная случайная величина X задана интегральной функцией:
Непрерывная случайная величина X задана интегральной функцией:
|
Ах4; при 0≤ x< 3
1; при х≥ 3
Найти: а) коэффициент А;
б) дифференциальную функцию f(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) Р(1≤ X≤ 2);
д) построить графики F(x) и f(x)
2. Вероятность появления события А в одном испытании равна 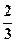 Составить: а) ряд распределения;
Составить: а) ряд распределения;
б) функцию распределения числа появления события А в 3-x
независимых испытаниях;
в) построить многоугольник распределения и график
функции распределения.
Найти: г) математическое ожидание, дисперсию, среднее
квадратическое отклонение рассматриваемой величины;
д) вероятность хотя бы 2-х появлений события А в
3-х испытаниях.
3. Агрегат содержит 2000 деталей. Вероятность выхода детали из строя за время работы агрегата равна 0, 001. Полагая, что число вышедших из строя деталей подчинено закону Пуассона, найти вероятность выхода из строя более одной детали.
4. Принимая вероятность рождения девочки равной 0, 6; найти вероятность того, что из 800 родившихся детей девочек будет 420.
5. Случайная величина X подчинена нормальному закону распределения с математическим ожиданием равным 50 и средним квадратическим отклонением равным 2. Определить вероятность того, что случайная величина примет значение превышающее 50.
6. Вероятность наступления события в каждом отдельном испытании равна 0, 2. Сколько испытаний нужно провести, чтобы с вероятностью не меньшей 0, 998 можно было ожидать отклонение относительной частоты события от его вероятности по абсолютной величине не более, чем на 0, 01?
7. Вычислить двумя способами М(2Х+1) и D(2X+1), если задан закон:
| x | |||
| p | 0, 2 | 0, 3 | 0, 5 |
Вариант 8.
1. Непрерывная случайная величина X задана дифференциальной функцией:
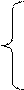 0; при х< -1
0; при х< -1
|
0; при х≥ 2
Найти: а) коэффициент А;
б) интегральную функцию F(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) Р(0< Х≤ 1);
д) построить графики F(x) и f(x)
2. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0, 1.
Составить: а) ряд распределения;
б) функцию распределения числа бракованных деталей
среди 3-х проверенных;
в) построить многоугольник распределения и график
функции распределения.
Найти: г) математическое ожидание, дисперсию, среднее
квадратическое отклонение рассматриваемой величины;
д) вероятность не более одной бракованной детали среди
3-х проверенных.
3. Среднее число вызовов, поступающих на АТС за 1 минуту равно 3. Найти вероятность того, что за 2 минуты поступит 5 вызовов, если число вызовов подчинено закону Пуассона.
4. Вероятность наступления события в каждом из независимых испытаний равна 0, 2. Проведено 900 испытаний. Найти вероятность того, что относительная частота появления события отклонится от его вероятности не более, чем на 0, 004.
5. Найти вероятность попадания в интервал (12; 14) нормального распределения случайной величины X, если известны ее математическое ожидание а=10 и среднее квадратическое отклонение σ =4.
6. Случайная величина X задана плотностью распределения:
|
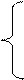
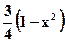 ; при -1≤ х< 1
; при -1≤ х< 1
Ах2; при x< -1 и х≥ 1
Оценить вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине не превысит 1, 5.
7. Вычислить двумя способами М(2Х-Y) и D(2X-Y), если заданы законы распределения:
| x | Y | ||||||
| p | 0, 1 | 0, 7 | 0, 2 | q | 0, 4 | 0, 6 |
Вариант 9.
1. Непрерывная случайная величина X задана интегральной функцией
|
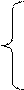 0; при х< 1
0; при х< 1
Ах-2; при 1≤ x< 1, 5
0; при х≥ 1, 5
Найти: а) коэффициент А;
б) дифференциальную функцию f(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) 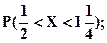
д) построить графики F(x) и f(x).
2. Производится три выстрела по мишени. Вероятность попадания при
каждом выстреле равна  .
.
Составить: а) ряд распределения;
б) функцию распределения числа попадания в мишень;
в) построить многоугольник распределения и график
функции распределения.
Найти: г) математическое ожидание, дисперсию, среднее
квадратическое отклонение рассматриваемой случайной
величины;
д) вероятность двух попаданий в мишень.
3. Как велико должно быть число испытаний, чтобы с вероятностью равной 0, 995 можно было ожидать, что относительная частота события А будет отличаться от его вероятности 0, 6, постоянной для всех испытаний, менее, чем на 0, 01 8 ту или другую сторону.
4. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной равна 0, 01. Найти вероятность того, что среди 200 деталей бракованных окажется не более трех.
5. Найти вероятность попадания в интервал (15; 25) нормально распределенной случайной величины X, если известны ее математическое ожидание а=20 и среднее квадратическое отклонение σ =5.
6. Математическое ожидание длины детали 50см, дисперсия 0, 1. В каких границах, с вероятностью не менее 0, 6 следует ожидать длину проверяемой детали.
7. Вычислить двумя способами М(Х+2Y) и D(X+2Y), если заданы законы распределения:
| x | Y | ||||||
| p | 0.1 | 0.7 | 0.2 | q | 0.4 | 0.6 |
Вариант 10
1. Непрерывная случайная величина X задана интегральной функцией:
|
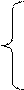 0; при х< 1
0; при х< 1
А(х2-2); при 1≤ x< 2
0; при х≥ 2
Найти: а) коэффициент А;
б) дифференциальную функцию f(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) Р(0< X≤ 1, 5);
д) построить графики F(x) и f(x).
2. Автомат штампует детали. Вероятность того, что не будет выпущено ни одной нестандартной детали равна 0, 9.
Составить: а) ряд распределения;
б) функцию распределения числа стандартных деталей
среди трех проверенных;
в) построить многоугольник распределения и график
функции распределения.
Найти: г) математическое ожидание, дисперсию, среднее
квадратическое отклонение рассматриваемой случайной
величины;
д) вероятность хотя бы двух бракованных деталей среди
трех проверенных
3. Среднее число кораблей, заходящих в порт за 1 час равно 2. Найти вероятность того, что за два часа в порт зайдет 5 кораблей (считать число кораблей, заходящих в порт, распределенным по закону Пуассона).
4. Вероятность появления события в каждом из независимых испытаний равна 0, 2. Найти число испытаний n, при котором с вероятностью 0, 9876 можно ожидать, что относительная частота появления события отклонится от вероятности по абсолютной величине не более чем на 0, 04.
5. Найти вероятность попадания в интервал (4; 9) нормально распределенной случайной величины X, если известны ее математическое ожидание а=2 и среднее квадратическое отклонение σ =5.
6. Дисперсия каждой из 2500 случайных величин не превышает 5. Оценить вероятность того, что отклонение средней арифметической их математически) ожиданий по абсолютной величине не превысит 0, 4,
7. Вычислить двумя способами М(2-ЗХ2), если задан закон распределения:
| x | |||
| p | 0.5 | 0.3 | 0.2 |
Вариант 11.
1. Непрерывная случайная величина X задана дифференциальной
функцией:
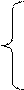 0; при х< 2
0; при х< 2
|
0; при х≥ 3
Найти: а) коэффициент А;
б) интегральную функцию f(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) 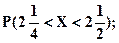
д) построить графики F(x) и f(x).
2. Составить: а) ряд распределения;
б) функцию распределения числа выпадений шестерки
при 4-х подбрасываниях игральной кости;
в) построить многоугольник распределения и
график функции распределения.
Найти: г) математическое ожидание, дисперсию, среднее
квадратическое отклонение рассматриваемой
случайной величины;
д) вероятность невыпадения шестерки при
4-х подбрасываниях игральной кости.
3. Среднее число вызовов, поступающих на АТС за 1 минуту равно 2. Найти вероятность того, что за 3 минуты поступит 3 вызова, если число вызовов распределено по закону Пуассона.
4. Вероятность поражения мишени стрелком при одном выстреле равна 0, 9. Найти вероятность того, что при 100 выстрелах стрелок поразит мишень не менее 80 и не.более 95 раз.
5. Найти вероятность попадания в интервал (6; 10) нормально распределенной случайной величины X, если известны ее математическое ожидание а=2 и среднее квадратическое отклонение σ =4.
6. Вероятность наступления события в каждом отдельном испытании равна 0, 2. Сколько испытаний нужно провести, чтобы с вероятностью не менее 0, 99 можно было ожидать отклонение относительной частоты события от его вероятности не более чем на 0, 02?
7. Вычислить двумя способами, пользуясь соответствующими свойствам! * и непосредственно M(XY+2), если заданы законы распределения двух независимых случайных величин:
| x | Y | |||||||
| p | 0, 4 | 0, 5 | 0, 1 | q | 0, 3 | 0, 5 | 0, 2 |
Вариант 12.
1. Непрерывная случайная величина X задана интегральной функцией:
|
 0; при х< 1
0; при х< 1
А(х-1); при 1≤ x< 3
1; при х≥ 3
Найти: а) коэффициент А;
б) дифференциальную функцию f(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) Р(1< Х≤ 2);
д) построить графики F(x) и f(x).
2. Составить: а) ряд распределения;
б) функцию распределения числа выпаданий герба при
шести подбрасываниях монеты;
в) построить многоугольник распределения и функции
распределения;
Найти: г) математическое ожидание, дисперсию, среднее
квадратическое отклонение рассматриваемой
случайной величины;
д) вероятность выпадения герба не менее двух и не более
пяти раз при шести подбрасываниях монеты.
3. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0, 003. Найти вероятность того, что магазин получит 5 разбитых бутылок
4. В урне содержатся белые и черные шары в отношении 4: 1. После извлечения шара регистрируется его цвет и шар возвращается в урну. Чему равно число извлечений n, при котором с вероятностью 0, 9722 можно ожидать, что абсолютная величина отклонения относительной частоты появления белого шара от его вероятности будет не более, чем 0, 01?
5. Найти вероятность попадания в интервал (3; 10) нормально распределенной случайной величины X, если известны ее математическое ожидание а=3 и среднее квадратическое отклонение σ =2.
6. Дисперсия каждой из 10000 независимых величин не превышает 5. Оценить вероятность того, что отклонение средней арифметической их математических ожиданий превысит 0, 04.
7. Вычислить двумя способами M(3XY-2), если заданы законы распределения двух независимых случайных величин:
| x | Y | ||||||
| p | 0, 2 | 0, 8 | q | 0, 5 | 0, 3 | 0, 2 |
Вариант 13.
1. Непрерывная случайная величина X задана интегральной функцией:
|
 0; при х< 2
0; при х< 2
А(х-2)2; при 2≤ x< 3
1; при х≥ 3
Найти: а) коэффициент А;
б) дифференциальную функцию f(x);
в) математическое ожидание, дисперсию, среднее
квадратическое отклонение;
г) 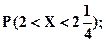
д) построить графики F(x) и f(x).
2. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равно 0, 8.
Составить: а) ряд распределения;
б) функцию распределения числа стандартных деталей
среди 4-х проверяемых;
в) построить многоугольник распределения и график
функции распределения;
Найти: г) математическое ожидание, дисперсию, среднее
квадратическое отклонение рассматриваемой
случайной величины;
д) вероятность не менее 3-х бракованных изделий среди
4-х.
3. Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно равна 0, 0001.Найти вероятность того, что тираж содержит 4 бракованных книги.
4. Вероятность появления события в каждом из 900 независимых испытаний равна 0, 5. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0, 01.
5. Найти вероятность попадания в интервал (1; 12) нормально распределенной случайной величины X, если известны ее математическое ожидание а=5 и среднее квадратическое отклонение σ =1.
6. Известию, что дисперсия каждой из данных независимых случайных величин не превышает 4. Определить число таких величин, при котором отклонения средней арифметической случайных величин от средней арифметической их математических ожиданий не более чем на 0, 25, превысит 0, 99.
7. Пользуясь свойствами, вычислить М(Х+2У), D(X+2У), если
| x | y | -1 | |||||
| p | 0, 4 | 0, 6 | q | 0, 3 | 0, 1 | 0, 6 |
X и У - независимые случайные величины.
Вариант 14.
1. Непрерывная случайная величина X задана дифференциальной функцией: