Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Взаимное расположение двух прямых на плоскости. Расстояние от точки до прямой
|
|
Пусть даны две прямые l 1 и l 2 на плоскости:
.
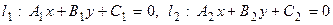Чтобы определить их взаимное расположение, достаточно решить систему уравнений:
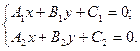(3.8)
Если эта система имеет единственное решение (х 0, у 0), то прямые l 1 и l 2, пересекается в точке М 0(х 0, у 0). Если система (3.8) не имеет решений, то прямые l 1 и l 2 не пересекаются, следовательно, l 1 || l 2. Если система (3.8) имеет бесконечное множество решений, то l 1 и l 2 совпадают.
Однако решить вопрос о взаимном расположении l 1 и l 2 можно и не решая системы (3.3). Действительно, из общего уравнения прямой l 1, находим, что ее нормальный вектор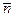 
имеет координаты А 1 и В 1, т.е. 
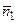= { А 1, В 1}, а прямая l 2 имеет нормальный вектор 
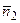= { А 2, В 2}. Если векторы 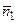, 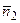коллинеарны, то прямые l 1 и l 2 либо параллельны, либо совпадают. Если 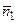, 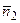неколлинеарны, то прямые пересекаются. Зная, что коллинеарные векторы (и только они) имеют пропорциональные координаты, получаем: если 
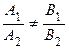, то прямые l 1 и l 2 пересекаются; если 
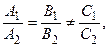то прямые l 1 и l 2 параллельны; если 
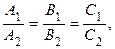то прямые l 1 и l 2 совпадают.
Используя нормальные векторы 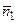, 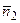можно также найти угол между прямыми, так как угол между нормальными векторами равен одному из углов 
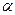между прямыми l 1 и l 2 (рис. 3.9).
Из определения скалярного произведения векторов получаем: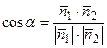 
, поэтому 
.
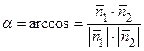Пусть на плоскости заданы прямая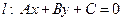 
и точка М 0(х 0, у 0). Найдем расстояние d от точки М 0(х 0, у 0) до прямой l (рис. 3.10). Пусть М 1(х 1, у 1) – точка пересечения прямой l и прямой, проходящей через точку М 0 перпендикулярно l. Так как М 1 лежит на l, то ее координаты удовлетворяют уравнению этой прямой, таким образом, имеем тождество:
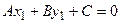. (3.9)
Рассмотрим вектор 
. Этот вектор коллинеарен нормальному вектору 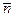= { А 1, В 1} прямой l и 
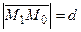, поэтому косинус угла между векторам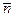и и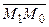 
равен либо 1, либо -1. Следовательно, 
, откуда
.
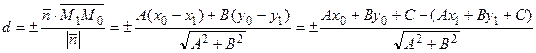Учитывая тождество (3.9) получаем:
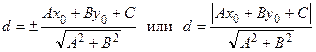. (3.10)
Пример 3.3. Найти расстояние от точки пересечения прямых l l и l 2 до прямой l 3. Определить взаимное расположение пар прямых l 1, l 3 и l 2, l 3, если прямые заданы общими уравнениями:
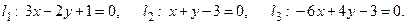
Решение. Решим систему уравнений:
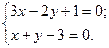
Получим: х 0 = 1, у 0 = 2 – единственное решение. Следовательно, прямые l 1 и l 2 пересекается в точке М 0(1, 2). Используя формулу (3.10), найдем расстояние d от М 0 до l 3:
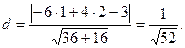
Нормальные векторы прямых l 1, l 2 и l 3 соответственно будут 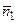= {3, –2}, 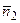= {1, 1}, 
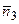= {–6, 4}. Так как координаты 
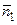и 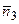пропорциональны 3/(– 6) = –2/3 и –2/4 
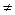1/(–3), то l 1 || l 3. Для 
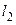и 
имеем: 1/(–6) 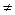1/4, следовательно, l 2 и l 3 пересекаются.