
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Взаимное расположение в пространстве двух прямых, прямой и плоскости
|
|
Пусть прямые l 1 и l 2 заданы каноническими уравнениями:
l 1: 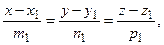 l 2:
l 2: 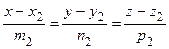 .
.
Направляющие векторы этих прямых соответственно будут:
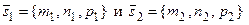
Углом между прямыми называется угол между прямыми, проведенными параллельно данным через какую-нибудь точку пространства. Один из смежных углов, очевидно, будет равен углу 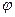 между направлявшими векторами
между направлявшими векторами 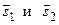 , который вычисляется по формуле (2.4):
, который вычисляется по формуле (2.4):
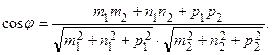
Условия параллельности и перпендикулярности прямых совпадают, соответственно с условиями параллельности или перпендикулярности векторов 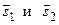 .
.
Чтобы определить взаимное расположение прямых l 1 и l 2 и найти точку их пересечения (если они пересекаются), достаточно решить систему уравнений с тремя неизвестными:
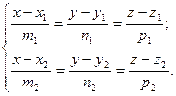
Если эта система имеет единственное решение х 0, у 0, z 0, то прямые пересекаются в точке М 0(х 0, у 0, z 0).
Если система имеет бесконечное множество решений, то прямые совпадают.
Если система не имеет решений, то прямые l 1 и l 2 не имеют общих точек, а потому либо параллельные, либо скрещивающиеся. Пусть заданы плоскость 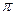 и прямая l:
и прямая l:
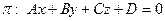 , l:
, l: 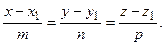
Если система из этих трех линейных уравнений с тремя неизвестными х, у, z имеет единственное решение, то l и 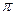 пересекаются; если система несовместна, то
пересекаются; если система несовместна, то 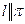 ; если система имеет бесконечное множество решений, то прямая l лежит в плоскости
; если система имеет бесконечное множество решений, то прямая l лежит в плоскости 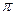 .
.
Условие параллельности l и 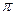 совпадает с условием перпендикулярности векторов
совпадает с условием перпендикулярности векторов 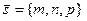 и
и 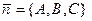 , т.е.
, т.е. 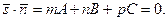
Условие перпендикулярности l и 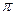 будет выглядеть так:
будет выглядеть так:
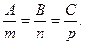 (Убедитесь в этом!).
(Убедитесь в этом!).
Пример 3.7. Выяснить взаимное расположение прямой l и плоскости 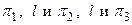 , если они заданы уравнениями:
, если они заданы уравнениями:
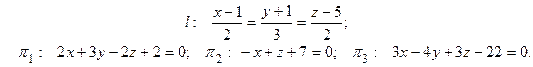
Решение. Запишем уравнения прямой l в параметрической форме:
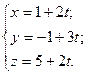 (3.16)
(3.16)
1) Подставим эти выражения в уравнение плоскости 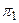 , получим:
, получим:
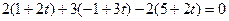 .
.
Решая это уравнение, получим t 1 = 1. Подставим это значение в систему (3.16) получим 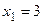 ,
, 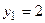 ,
, 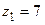 . Следовательно, прямая и плоскость пересекаются в точке М 1(3, 2, 7).
. Следовательно, прямая и плоскость пересекаются в точке М 1(3, 2, 7).
2) Подставим х, у, z из (3.16) в уравнение плоскости 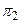 :
:
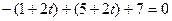
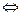
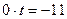 .
.
Получили противоречивое уравнение, значит, соответствующая система решенийне имеет, а поэтому 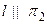 .
.
3) Подставим х, у, z из системы (3.16) вуравнение плоскости 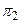 :
:
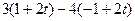
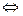
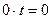 ,
,
отсюда видно, что параметр t может принимать любые значения, при этом соответствующая точка прямой l принадлежит плоскости 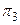 . Значит, прямая l лежит в плоскости
. Значит, прямая l лежит в плоскости 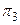 .
.