Приведите к каноническому виду уравнения линий второго порядка. Установите тип этих линий и их расположение. Сделайте схематический чертеж.

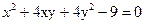
Решение.

, ,

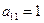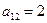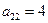
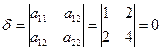
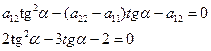
D=9-4·2·(-2)=25

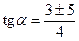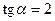· или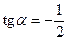

Будем рассматривать 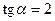, тогда

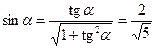
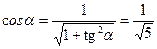
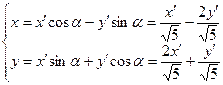
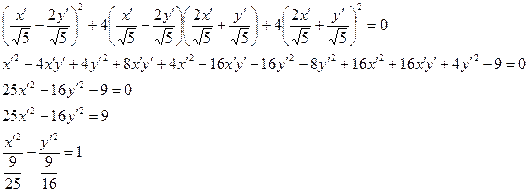
Получили уравнение гиперболы

Решить систему линейных уравнений матричным методом и методом Гаусса. Сделать проверку.

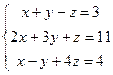
Решение.

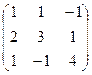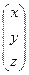1)Для решения матричным методом нужно рассмотреть матричное уравнение: AX = B, где A = , X = , B = 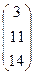. Тогда X = A^-1B. Найдем матрицу A^-1.

Вычислим обратную матрицу .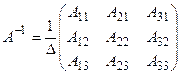

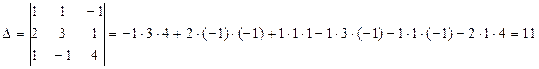
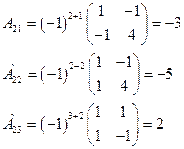
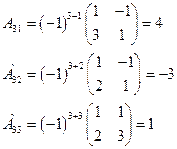
Тогда A^-1 =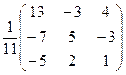

Получим

X = A^-1B = = = .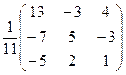

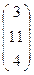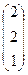2) Для решения системы методом Гаусса приведем матрицу к треугольному виду.

Рассмотрим расширенную матрицу системы и приведем ее к треугольному виду:

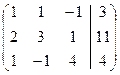= [умножаем первую строчку на -2 и складываем со второй, умножаем первую на -1 и складываем с третьей] = 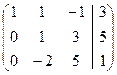= умножаем вторую строку на 2 и складываем с третьей] =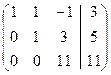

Получаем систему:

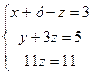
Получаем х=2, у=2, z=1.

Проверка: Подставим полученные значения переменных в исходную систему уравнений:

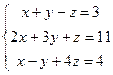
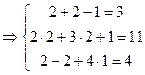Получаем верные равенства

Ответ: х=2, у=2, z=1