Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение ошибки выборки при различных способах отбора
|
|
При решении задач выборочного наблюдения обязательным этапом является определение ошибки выборки. Формулы для ее определения разработаны теорией вероятности и математической статистикой.
При собственно-случайном способе отбора обследованию подвергаются единицы совокупности без предварительного систематизирования.
Средняя ошибка выборки для среднего размера признака определяется по формулам 8.1 и 8.2.
При повторном способе:
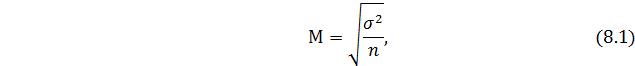
При бесповторном способе:
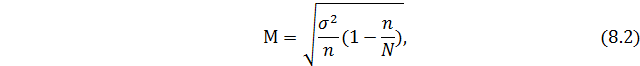
где 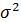 - дисперсия;
- дисперсия;
n – объем выборочной совокупности;
N – объем генеральной совокупности.
Предельная (абсолютная ошибка выборки) находится по формуле:
 , (8.3)
, (8.3)
где t – коэффициент доверия, который определяется по таблице
значений функции Лапласа при заданной
доверительной вероятности.
Относительная ошибка выборки определятся с использованием формулы:
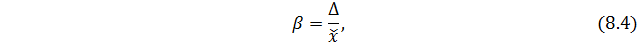
где 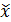 - среднее значение признака в выборочной совокупности.
- среднее значение признака в выборочной совокупности.
Считается, что если β превышает 12%, то погрешность высокая и необходимо увеличить объем выборки.
Зная величину выборочной средней и предельную ошибку выборки, определяется доверительный интервал, в котором находится значение генеральной средней:
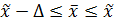 +
+ 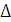 , (8.5)
, (8.5)
где 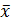 – средний размер признака в генеральной совокупности.
– средний размер признака в генеральной совокупности.
При проектировании выборочного наблюдения решается задача нахождения необходимой численности выборки, обеспечивающей определенную точность расчета оценок генеральной средней.
Сначала задается величина относительной ошибки выборки (β), затем определяется абсолютная ошибка (Δ) при заданном значении β:

Затем находится объем выборки при повторном способе:
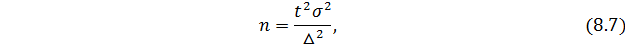
При бесповторном способе объем выборки определяется:
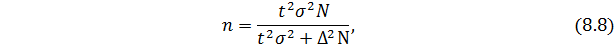
При определении ошибки доли единиц, которые обладают определенным признаком, используется формула:
- при повторном способе:
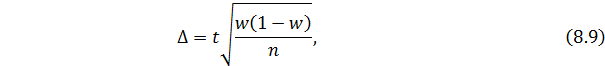
- при бесповторном способе:
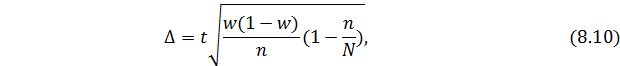
где w – доля единиц, обладающих каким-либо значением признака в
выборочной совокупности.
Значение генеральной доли (P) будет находиться в доверительном интервале:
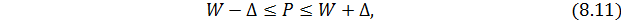
Пример 1. Для определения средней продолжительности междугородних телефонных разговоров из 1300 предоставленных абонентам разговоров в случайном порядке было отобрано 316. Результаты этого наблюдения представлены в таблице 8.1.
Таблица 8.1
| Продолжительность междугородних телефонных разговоров, мин. | Количество разговоров |
| До 3 3-5 5-7 7-9 9-11 11-13 13-15 | |
| Итого |
По данным ряда распределения определить:
- среднюю протяженность разговоров;
- ошибку средней при вероятности 0, 99;
- объем выборки при заданном значении β =4%.
Способ отбора бесповторный.
Решение:
По средней арифметической взвешенной определено, что средняя продолжительность разговоров составляет 6, 7 мин., а дисперсия 7, 3 мин.
Абсолютная ошибка выборки составит:
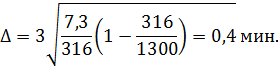
Значение коэффициента доверия t=3 взято из таблицы в зависимости от заданной вероятности равной 0, 99.
Относительная ошибка выборки:
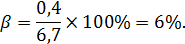
Интервал, в котором находится генеральная средняя:
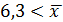
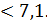
Определяется объем выборки при заданном β =4%.
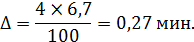
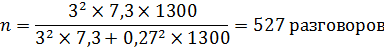
при β =4% необходимо взять в выборку 527 разговоров.
Пример 2. На предприятии работает 1250 человек, проведено бесповторное выборочное наблюдение и отобрано 280 человек, из них 105 человек прошли техническое обучение. Определить долю работников, прошедших техническое обучение при вероятности 0, 995. Выборка бесповторная.
Доля работников, прошедших обучение в выборке:
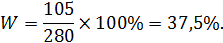
Ошибка доли:
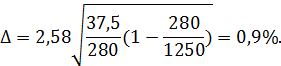
Интервал, в котором находится генеральная доля:
36, 6 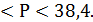
Относительная ошибка выборки составит:
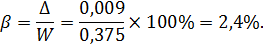
Погрешность небольшая.
Механический способ отбора отличается от собственно-случайного тем, что исследуемые единицы сначала систематизируются, а потом отбираются или каждая пятая, или десятая единица в группе. Механический способ бывает только бесповторный, а формулы определения ошибки выборки аналогичны собственно-случайному способу.
Серийный способ отбора является групповым способом. Отбор производится случайно, целыми группами или сериями. В отобранных сериях обследованию подвергаются все единицы.
Ошибки средней величины при серийном способе определяются по формулам:
- при повторном способе:
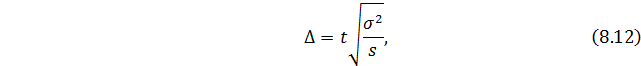
- при бесповторном способе:
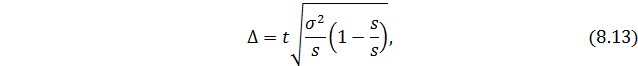
где s – количество серий в выборочной совокупности;
S – количество серий в генеральной совокупности.
Типический способ предполагает, что вначале вся совокупность разбивается на группы по определенному признаку, а затем в каждой группе в случайном порядке отбираются отдельные единицы.
Формула для определения ошибки выборки при этом способе следующая:

где 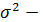 средняя из групповых дисперсий.
средняя из групповых дисперсий.
Малой выборкой считается такая выборка, в которой количество отобранных единиц не превышает 20. Ошибка в малой выборке (Δ *) определяется по формуле:
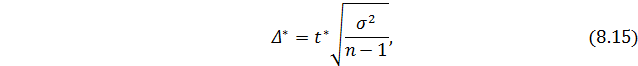
где 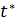 - коэффициент доверия, который находится по таблице
- коэффициент доверия, который находится по таблице
Стьюдента в зависимости от заданной вероятности и объема
выборки.
Вопросы для самопроверки
1. Какие существуют способы проведения выборочного наблюдения?
2. Какие факторы влияют на величину ошибки выборки?
3. Каким образом переносятся результаты выборочного наблюдения на генеральную совокупность?
4. Что показывает относительная ошибка выборки?
5. Каким образом находится необходимый объем выборки?
6. Чем отличается расчет ошибки в малой выборке от расчета ошибки, которая находится в большой выборке?
7. С точки зрения достоверности, какая выборка предпочтительнее: бесповторная или повторная?
Тест для самопроверки к теме 8 «Выборочное наблюдение»
1. При определении ошибки выборки откуда берется коэффициент доверия:
1. определяется по формуле
2. определяется по графику
3. находится по специальным таблицам
2. Какая ошибка выборочного наблюдения характеризует величину погрешности:
1. абсолютная
2. относительная
3. Имеются несколько формул для определения ошибки доли единиц, которые обладают данным признаком. Выбрать правильную формулу (выборка бесповторная):