Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод потенциалов. (1.8.1) В методе потенциалов каждому пункту отправления приписывается потенциал
|
|
|
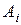приписывается потенциал 
, а пункту назначения 
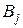- потенциал 
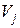так, что
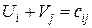
для каждой базисной клетки. Так как потенциалов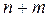 
, а базисных клеток 
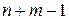, то одному из потенциалов (любому) придают произвольное значение, как правило, нулевое. Остальные находятся из равенств (1.8.1).
|
.
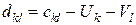(Докажите самостоятельно, что так вычисленное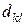 
совпадает с соответствующей оценкой свободной клетки в распределительном методе).
Алгоритм решения транспортной задачи методом потенциалов состоит в следующем.
1. Находится начальный план (любым способом).
2. Для каждого пункта отправления и каждого пункта назначения находятся потенциалы.
3. Для каждой свободной клетки вычисляется оценка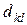 
.
4. Если все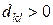 
, то найденное распределение перевозок дает минимальную стоимость.
5. Если среди оценок 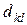есть отрицательные, то для клетки 
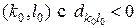, наибольшей по модулю, строится цикл и производится сдвиг по циклу (как и в распределительном методе). Затем переходят к новому распределению перевозок, возвращаясь к п.2.
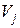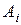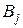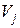Замечание. Удобно и записывать в таблицах напротив соответствующих и , а вычисления и производить в уме.
Пример 3. Найти методом потенциалов оптимальное распределение перевозок транспортной задачи, приведенной в табл. 1.8.1.
Таблица 1.8.1
| Пункты | B1 | B2 | B3 | B4 | B5 | Наличие |
| А1 | --- | --- | --- | --- | --- | |
| А2 | --- | --- | --- | --- | --- | |
| А3 | --- | --- | --- | --- | --- | |
| Потребности |
Начальный опорный план найдем методом северо-западного угла (табл. 1.5.2).
Таблица 1.8.2
| Пункты | B1 | B2 | B3 | B4 | B5 | Наличие | |
| Потенциалы | V1=2 | V2=1 | V3=2 | V4=3 | V5=1 | ||
| А1 | U1=0 | --- | --- | --- | |||
| А2 | U2=-1 | --- | --- | ||||
| А3 | U3=0 | --- | --- | --- | |||
| Потребности |
Стоимость перевозок по этому плану равна
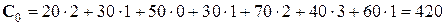ед.
и 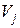по формуле (1.8.1). Занесем потенциалы в табл. 1.8.2. Найдем оценки 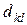для свободных клеток:
,
,
,
,
,
,
,
.
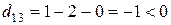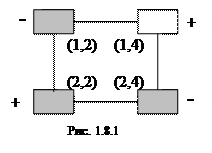
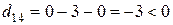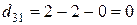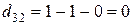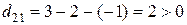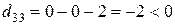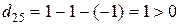Наибольшая по модулю отрицательная оценка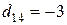 
. Производим сдвиг по циклу на 
и переходим к табл. 1.8.3.
Таблица 1.8.3
| Пункты | B1 | B2 | B3 | B4 | B5 | |
| Потенциалы | V1=2 | V2=-2 | V3=-1 | V4=0 | V5=-2 | |
| А1 | U1=0 | --- | --- | --- | ||
| А2 | U2=2 | --- | --- | |||
| А3 | U3=3 | --- | --- | --- |
Стоимость перевозок по новому плану уменьшилась и стала равной
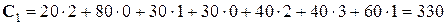ед.
Для проверки оптимальности плана найдем потенциалы и оценки свободных клеток. Примем U1=0, вычислим остальные и 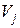и занесем их в табл. 1.8.3. Вычислим 
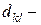оценки свободных клеток:
, 
,
, 
,
, 
,
, 
.
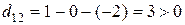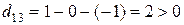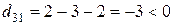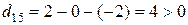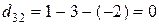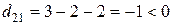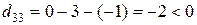Вводим в базис клетку (3, 1), производя сдвиг по циклу на 20ед.
Переходим к (табл. 1.8.4.)
Таблица 1.8.4
| Пункты | B1 | B2 | B3 | B4 | B5 | |
| Потенциалы | V1=-1 | V2=-2 | V3=-1 | V4=0 | V5=-2 | |
| А1 | U1=0 | --- | --- | --- | ||
| А2 | U2=2 | --- | --- | |||
| А3 | U3=3 | --- | --- | --- |
Стоимость перевозок по новому плану уменьшилась и стала равной
ед.
Проверим оптимальность. Вычислим потенциалы, занесем в табл.14. Найдем 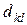для свободных клеток
, ,
, ,
, ,
, .
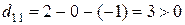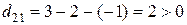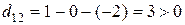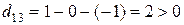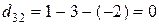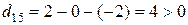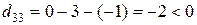Вводим в базис клетку (3, 3), производя сдвиг по циклу на 20ед.
Переходим к табл. 1.8.5.
Таблица 1.8.5
| Пункты | B1 | B2 | B3 | B4 | B5 | |
| Потенциалы | V1=1 | V2=-2 | V3=-1 | V4=0 | V5=0 | |
| А1 | U1=0 | --- | --- | --- | --- | |
| А2 | U2=2 | --- | --- | |||
| А3 | U3=1 | --- | --- |
Стоимость перевозок по новому плану уменьшилась и стала равной
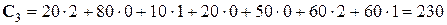ед.
Проверим оптимальность. Примем U1=0, вычислим остальные и 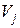и занесем их в табл. 1.8.5. Найдем 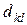для свободных клеток
, 
,
, 
,
, 
,
, 
.
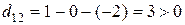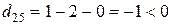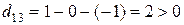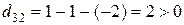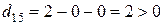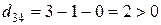Вводим в базис клетку (2, 5) и получаем табл. 1.8.6.
Таблица 1.8.6
| Пункты | B1 | B2 | B3 | B4 | B5 | |
| Потенциалы | V1=0 | V2=-2 | V3=-2 | V4=0 | V5=-1 | |
| А1 | U1=0 | --- | --- | --- | --- | |
| А2 | U2=2 | --- | --- | |||
| А3 | U3=2 | --- | --- |
Стоимость перевозок по новому плану уменьшилась и стала равной
ед.
Проверим оптимальность. Примем U1=0, вычислим остальные и 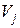и занесем их в табл. 1.8.6. Найдем 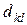для свободных клеток
, 
,
, 
,
, 
,
, 
.
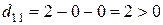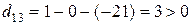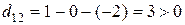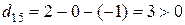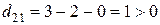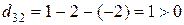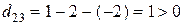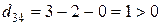Так как все оценки свободных клеток неотрицательны, то полученный в табл.16 план распределения перевозок является оптимальным.
Минимальная стоимость перевозок равна 
ед.
Замечание. Все рассмотренное ранее относится к замкнутой транспортной задаче, когда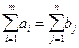 
. В открытой транспортной задаче 
. Решение таких задач сводится к решению замкнутых транспортных задач. Делается это следующим образом.
Если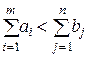 
, то вводим фиктивный пункт отправления 
с запасам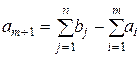и 
и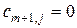 
. Если 
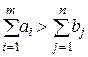, то вводим фиктивный пункт назначения 
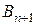с потребностями 
и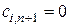 
.