Условие

Условие

Найти напряженность Н магнитного поля в точке, отстоящей на расстоянии а=2 м от бесконечно длинного проводника, по которому течет ток I=5 А.

Решение:

Напряженность магнитного поля, созданного бесконечно длинным прямоугольным проводником:

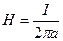, где а – расстояние от точки, где ищется напряженность, до проводника с током.

Ответ: Н=0, 398 А/м

Задача 2

Условие

Найти напряженность Н магнитного поля в центре кругового проволочного витка радиусом R= 1cм, по которому течет ток I=1А.

Решение:

,

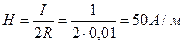где Н - напряженность магнитного поля в центре кругового тока;

R- радиус кругового контура с током.

Ответ: Н=50А/м

Задача 3

Условие:

На рисунке изображены сечения двух прямолинейных бесконечно длинных проводников с токами. Расстояние между проводниками АВ=10см, токи I₁=20А и I₂=30А. Найти напряженность Н магнитного поля, вызванного токами I₁ и I₂ в точках М₁ , М₂ и М₃. Расстояние М₁А=2 см, АМ₂ = 4см и ВМ₃= 3см.

Рисунок:

Решение:

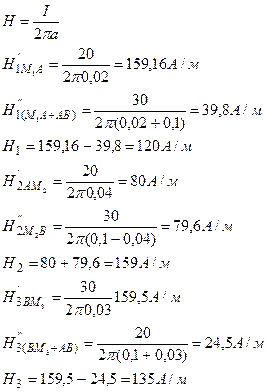
Ответ: Н₁=120А/м; Н₂=159А/м; Н₃=135А/м.

Занятие №2

Задача 1

Условие:

Найти напряженность Н магнитного поля на оси кругового контура на расстоянии а=3см от его плоскости. Радиус контура R=4см, ток в контуре I=2А.

Решение:

Напряженность магнитного поля на оси кругового тока:

,

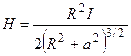где R- радиус кругового контура с током,

а – расстояние от точки, где ищется напряженность до плоскости контура

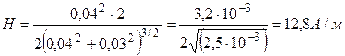
Ответ: Н=12, 8А/м

Задача 2

Условие:

Напряженность Н магнитного поля в центре кругового витка Н₀=0, 8 Э. Радиус витка R=11см. Найти напряженность Н магнитного поля на оси витка на расстоянии а=10см от его плоскости.

Решение:

Н₀=0, 8 Эрстед=0, 8·79, 5775А/м

Напряженность в центре кругового тока:

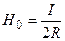=> I=2RH₀

I=2·0, 8·79, 5775·0, 11=14, 01A

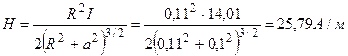
Ответ: Н=25, 79 А/м

Задача: 3

Условие:

Из проволоки длиной l= 1м сделана квадратная рамка. По рамке течет ток I=10А. Найти напряженность Н магнитного поля в центре рамки.

Решение:

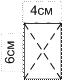
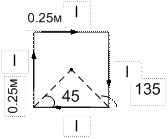Магнитное поле в центре рамки создается каждой из его сторон и направлено в одну сторону нормально к плоскости рамки, следовательно Н=4·Н₁, Н₁ – напряженность поля создаваемого отрезками проводника с током I длиной l /4, которая определяется по формуле: 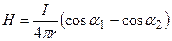, где r= l /2·4 – расстояние от проводника до точки поля. По условию α ₁=45°, α ₂=180-45=135°; тогда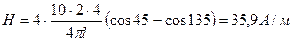

Ответ: Н=35, 9 А/м

Занятие №3

Задача №1

Условие:

По двум бесконечно длинным прямым проводникам, расстояние между которыми 15см, в одном направлении текут токи 4 и 6А. Определить расстояние от проводника с меньшей силой тока до геометрического места точек, в котором напряженность магнитного поля =0.

Решение:

Точка где Н₁=Н₂, расположена на прямой соединяющей проводники с током, т.е.

Напряженность магнитного поля, созданного бесконечно длинным проводником:

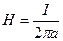и Н₁=Н₂ =>

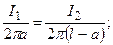I₁ (l-a)= I₂a I₁l=a(I₂+I₁) =>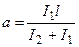

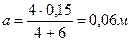
Ответ: а =0, 06м

Задача №2

Условие:

По двум бесконечно длинным прямым проводникам, расстояние между которыми 15см, в противоположных направлениях текут токи 4 и 6А. Определить расстояние от проводника с меньшей силой тока до геометрического места точек, в котором напряженность магнитного поля =0.

Решение:

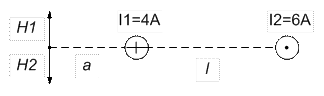
Точка где Н₁=Н₂ находится на продолжении прямой, соединяющей проводники с током

=>

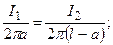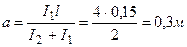
Ответ: а =0, 3м

Задача №3

Условие:

Под действием однородного магнитного поля, перпендикулярно линиям индукции начинает перемещаться прямой проводник массой 2кг, сила тока в котором 10А. Какой магнитный поток пересекает этот проводник к моменту времени, когда его скорость станет равна 31, 6 м/с?

Решение:

Работа перемещения проводника с током в магнитном поле равна A=IΔ Ф, где Δ Ф – магнитный поток, пересекаемый проводником при его движении. Эта работа будет численно равна кинетической энергии, приобретаемой проводником.

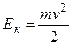; А=Е_к

=>

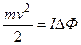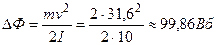
Ответ: Δ Ф=99, 86Вб.

Занятие №4

Задача №1.

Условие:

В однородном магнитном поле напряженностью Н=79, 6 кА/м помещена квадратная рамка, плоскость которой составляет с направлением магнитного поля угол α =45°, сторона рамки а =4см. Найти поток, пронизывающий рамку.

Решение:

Магнитная индукция: (1) В=μ ₀μ Н, где μ ₀ – магнитная постоянная μ ₀=125663·10^-7Гн/м. μ – относительная магнитная проницаемость (для вакуума μ =1, для воздуха μ =10000004).

Магнитный поток сквозь контур: (2) Ф=BScosφ, где S – площадь поперечного сечения контура, φ – угол между нормалью к плоскости контура и направлением магнитного поля.

(1) подставляем в (2) и получаем: Ф=μ ₀μ НScosφ, так как рамка квадратная, то площадь рамки S= а² => Ф=μ ₀ μ Н а² cosφ =12, 57·10^-7·1·79, 6·10³·0, 04²·cos45°=113мкВб.

Ответ: Ф=113мкВб.

Задача №2

Условие:

Квадратная рамка со стороной 4см содержит 100 витков и помещена в однородное магнитное поле напряженностью 100А/м. направление поля составляет угол 30° с нормалью к рамке. Ток в рамке равен 1А. Какая работа совершается при повороте рамки в положение, когда ее плоскость совпадает с направлением линий индукции поля.

Решение:

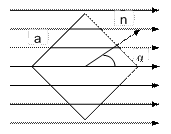
Когда плоскость рамки совпадает с направлением поля, угол α ₁ между вектором и нормалью 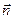равен 90°. Работа А поворота рамки с током I равна: А=IΔ ФN, Δ Ф=Ф-Ф₀ - изменение магнитного потока Ф, пронизывающего плоскость рамки, Ф=ВScosα, где

В= μ ₀μ Н – магнитная индукция; S= а ² – площадь рамки. Поток Ф₀, пронизывающий рамку в исходном положении, будет Ф₀=ВScosα ₀, а после поворота – Ф=DScosα ₁.

A=IΔ ФN=I(Ф-Ф₀)N=INBS(cosα ₁-cosα ₀)=INμ 0μ H a²( cosα ₁-cosα ₀)

A=1·100·12, 56·10^-7·1·100·0, 04²·(cos90-cos30)=-1, 7·10^-5Дж.

Ответ: А=-1, 7·10^-5Дж.

Задача №3

Условие:

В прямоугольной рамке со сторонами 4 и 6см сила тока 5А. Определить напряженность магнитного поля в центре рамки.

Решение:

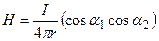
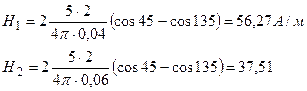
Н=Н₁+Н₂=56, 27+37, 51=93, 8А/м

Ответ: Н=93, 8А/м.

Занятие №5

Задача №1

Условие:

Сколько ампер-витков потребуется для того, чтобы внутри соленоида малого диаметра и длиной l =30см, объемная плотность энергии магнитного поля была равна W₀=1, 75Дж/м³.

Решение:

=>

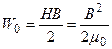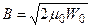
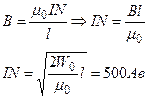
Ответ: IN=500Ав.

Задача №2

Условие:

соленоид имеет длину 1м, площадь поперечного сечения 25мм² и число витков 1000. Энергия поля соленоида при силе тока 1А равна 1, 9Дж. Определить магнитную проницаемость сердечника.

Решение:

H=In

Объемная плотность энергии магнитного поля: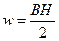

Энергия магнитного поля соленоида: W=wSl

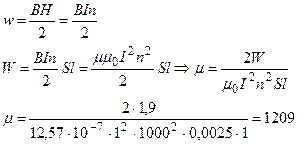
Ответ: μ =1209.

Задача №3

Условие:

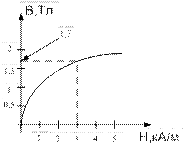
Соленоид длиной 20см и диаметром 4см имеет плотную трехслойную обмотку из провода диаметром 0, 1мм. По обмотке соленоида течет ток 0, 1А. Зависимость В=f(H) для материала сердечника дана на рис. Определить напряженность и индукцию поля в соленоиде, магнитную проницаемость и индукцию поля в соленоиде, магнитную проницаемость сердечника, индуктивность соленоида, энергию и объемную плотность энергии поля соленоида.

Решение:

Поле внутри соленоида считать однородным:

Н=In, где 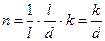- число витков, приходящихся на единицу длины соленоида; k – число слоев обмотки; d – диаметр провода. Тогда: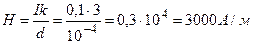

По рисунку находим В=1, 7Тл для Н=3000А/м

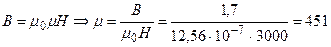
Индуктивность соленоида: L=μ μ ₀n²lS, где l – длина, 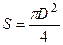- площадь поперечного сечения соленоида.

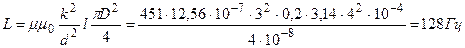
Объемная плотность энергии магнитного поля:

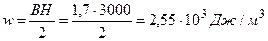
Энергия мгнитного поля соленоида:

W=wSl или .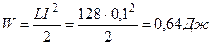

Ответ: H=3000A/м; L=128Гц; μ =451; w=2, 55·10³Дж/м³; W=0, 64 Дж.

Занятие №6

Задача №1

Условие:

Соленоид без сердечника длиной 15см и диаметром 4см имеет 100 витков на 1см длины, и включен в цепь источника тока. За 1мс сила тока в цепи изменилась на 10 мА. Определить ЭДС самоиндукции, считая что ток в цепи изменяется равномерно.

Решение:

ЭДС самоиндукции: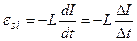

Индуктивность соленоида: L=μ μ ₀n²lS, где

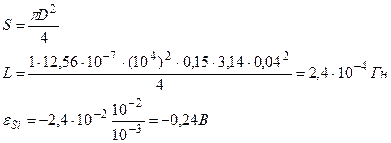
Ответ: .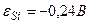

Задача№2

Условие:

в соленоиде сила тока равномерно возрастает от 0 до 100А в течение 2с и при этом индуцируется 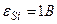. Какую энергию накопит поле соленоида в конце возрастания силы тока?

Решение:

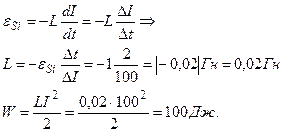
Ответ: W=100Дж.

Задача №3

Условие:

По обмотке соленоида с параметрами: число витков 1000, длина 0, 5м, диаметр 4см течет ток 0, 5А. Определить потокосцепление, энергию, объемную плотность энергии соленоида.

Решение:

n=2000;

H=In=0, 5·2000=1000А/м

Объемная плотность энергии:

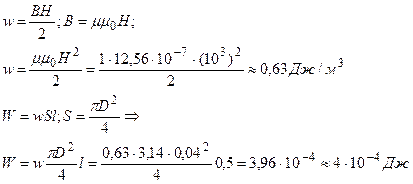
Потокосцепление:

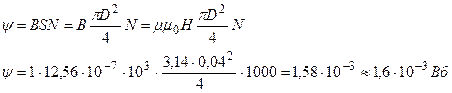
Ответ: W=4·10^-4Дж; w=0, 63Дж/м³; ψ =1, 6·10^-3Вб.