Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Устройство нивелира.
|
|
Рис. 63. Точный нивелир Н-3 с цилиндрическим уровнем при зрительной трубе: 1 – подъемные винты; 2 – круглый уровень; 3 – элевационный винт; 4 – окуляр зрительной трубы с диоптрийным кольцом; 5 – визир; 6 – кремальера; 7 – объектив зрительной трубы; 8 – закрепительный винт; 9 – наводящий винт; 10 – контактный цилиндрический уровень; 11 – юстировочные винты цилиндрического уровня
Точность изображения расстояний на планах и картах.
Точность определения расстояний по карте зависит от масштаба карты, характера измеряемых линий (прямые, извилистые), выбранного способа измерения, рельефа местности и других факторов.
Наиболее точно определить расстояние по карте можно по прямой линии.
При измерении расстояний с помощью циркуля-измерителя или линейкой с миллиметровыми делениями средняя величина ошибки измерения на равнинных участках местности обычно не превышает 0, 7-1 мм в масштабе карты, что составляет для карты масштаба 1: 25000 - 17, 5-25 м, масштаба 1: 50000 – 35-50 м, масштаба 1: 100000 – 70-100 м.
В горных районах при большой крутизне скатов ошибки будут больше. Это объясняется тем, что при съемке местности на карту наносят не длину линий на поверхности Земли, а длину проекций этих линий на плоскость.
| При определении длины маршрута по карте следует учитывать, что расстояния по дорогам, измеренные на карте с помощью циркуля или курвиметра, в большинстве случаев получаются короче действительных расстояний. Это объясняется не только наличием спусков и подъемов на дорогах, но и некоторым обобщением извилин дорог на картах. Поэтому получаемый по карте результат измерения длины маршрута следует с учетом характера местности и масштаба карты умножить на коэффициент, указанный в таблице. |
| Характер местности | Коэффициент увеличения длины маршрута, измеренного по карте масштаба | ||
| 1: 50000 | 1: 100000 | 1: 200000 | |
| Горная (сильнопересеченная) | 1, 15 | 1, 20 | 1, 25 |
| Холмистая (среднепересеченная) | 1, 05 | 1, 10 | 1, 15 |
| Равнинная (слабопересеченная) | 1, 00 | 1, 00 | 1, 05 |
Точность изображения расстояний на плане.
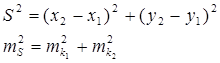Если отдельные точки на плане имеют погрешности положения, то расстояния между этими точками будут определены с погрешностью. Для определения зависимости погрешности расстояния между точками от погрешностей их положения представим, что каждая из точек определяется координатами Х1и У1, Х2 и У2 со своими СКП. Учитывая, что mt=mk√ 2, mk=mt/√ 2
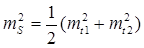
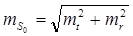- если mt1=mt2=mt, mS=mt, т. е. точность расстояния будет соответствовать точности положения контурных точек.
17. Прямоугольная система координат Гаусса – Крюгера.
На территории России используется проекция Гаусса – Крюгера. В этой проекции поверхность эллипсоида вращения делится на зоны геодезическими меридианами. В нашей стране установлены размеры зон в шесть и три градуса по долготе. Первые считаются основными, поэтому математическая обработка результатов измерений и оформление материалов топосъемок выполняются в шестиградусных зонах. Трехградусные зоны используются при производстве крупномасштабного картографирования (масштабов 1: 5 000 и крупнее) и вводе систем региональных плоских прямоугольных координат. Меридианы, проходящие посередине зон, называются осевыми.
Недостатков у проекции Гаусса – Крюгера, по мнению специалистов, два. Во-первых, в данной системе координат возникают трудности при математической обработке результатов полевых измерений на объектах, вытянутых вдоль параллели и занимающих значительную площадь (объектах, расположенных в нескольких зонах). Во-вторых, действительные плоские прямоугольные координаты не дают представления о том, где на поверхности земли находится точка. Она может располагаться в любой из 60 шестиградусных зон. Для того чтобы по значениям координат можно было судить о местоположении точки на Земле, в каталогах координат пунктов принято помещать так называемые условные координаты Гаусса – Крюгера: x', y'. При этом действительные и условные координаты связаны соотношениями [1–4]:
x' = x,
y' = n ⋅ 10^6 + 5 ⋅ 10^5 + y.
Действительные и условные абсциссы равны. Для получения условной ординаты надо к действительной прибавить номер зоны, умноженный на 106, и 500 000. Перенос начала координат к востоку на 500 километров необходим для исключения отрицательных ординат.