Показательные неравенства.

Методические указания.

Пусть а – фиксированное число, такое, что а > 0 и 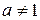. Рассмотрим неравенства

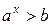(1)

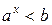(2)

Область допустимых значений этих неравенств совпадает со всей числовой прямой, функция 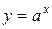положительна и строго монотонна, следовательно, при неравенство (1) выполняется при любом х из области допустимых значений, а неравенство (2) не имеет решений. При 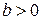приходится рассмотреть два случая: а > 1 и 1 > a > 0.

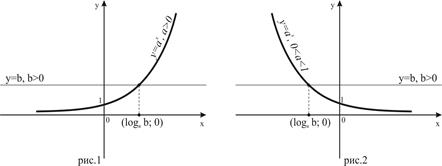
Пусть а > 1, тогда на всей числовой прямой функция 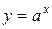является возрастающей (рис.1). Значение, равное b, она принимает в единственной точке 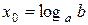, и поэтому решением неравенства (1) является все 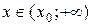, а решением неравенства (2) – все .

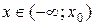Пусть 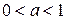, тогда на всей числовой прямой функция 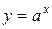является убывающей (рис.2), и поэтому решением неравенства (1) являются все 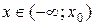, а решением неравенства (2) – вс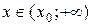е , где .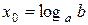

Пример 1. Для каждого значения а решить неравенство

.

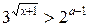Решение.

Запишем неравенство в виде:

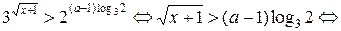
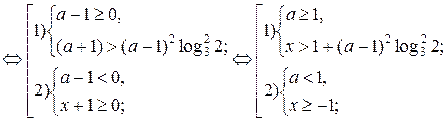
Ответ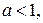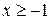: при ; при ,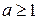

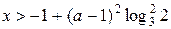
Таким образом, различные типы показательных неравенств сводятся к решению простейших показательных неравенств.

Рассмотрим неравенство вида:

.

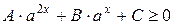Решение.

Обозначив 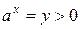, получим 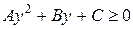. Пусть решение последнего неравенства имеет вид:

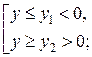
где 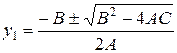и .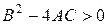

Тогда простейшее неравенство не имеет решений, а неравенство 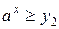решается по схеме 1. Сразу выпишем в этом случае ответ.

Ответ: при , ;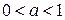

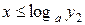при ,

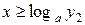
Заметим, что в предложенных выше схемах при решении неравенств многократно использовалось свойство положительности функции .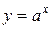

Пример.

Решить неравенство .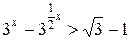

Решение.

Преобразуем неравенство 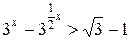. В обозначениях 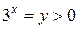, 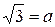неравенство примет вид:

.

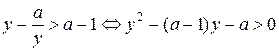Найдем корни соответствующего уравнения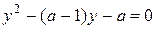

,

, .

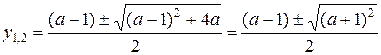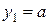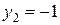Причем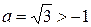

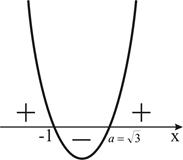
Значит неравенство равносильно совокупности

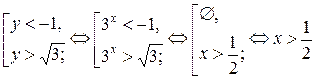
Ответ: .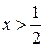

Рассмотрим следующий тип неравенств: .

Решение.

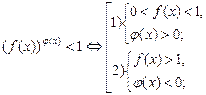
Аналогично решается и неравенство вида .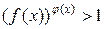

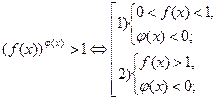
Пример.

Решить неравенство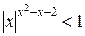

Решение.

По данной схеме неравенство равносильно совокупности двух систем:

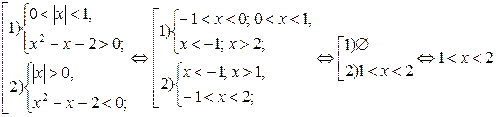
Ответ: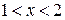

Кроме предложенных выше видов неравенств, предлагается решить графически неравенства, которые нельзя решить аналитически.

Пример.

а)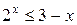

б)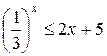

Решение.

а)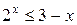

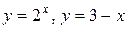
1. 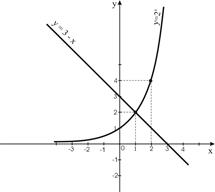Построим графики функци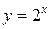й и .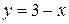

2. Найдем точки пересечения графиков функций .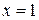

3. Решением данного неравенства будут те значения х, для каждого из которых график функции 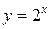лежит ниже графика .

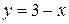Ответ: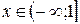

б)

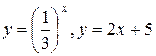
1. 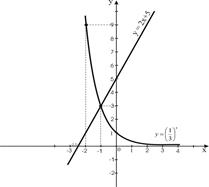Построим график функций .

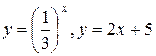2. Найдем точки пересечения графиков функций.

3. Решением данного неравенства будут те значения х, для каждого из которых график функции 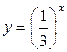лежит ниже графика .

Ответ: 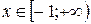.