
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нахождение экстремумов функции
|
|
Литература
1. Богомолов Н.В. Практические занятия по математике. – М.: Высш. шк., 2009
2. П.Т.Апанасов, М.И.Орлов. Сборник задач по математике. – М.: Высш. шк., 2009
Методические указания
Исследование функций с помощью производной. Нахождение промежутков монотонности
Теорема1. Если функция f(x) определена и непрерывна на промежутке (а; b) и f ‘(x) всюду положительна (f ‘(x)> 0), тогда функция возрастает на промежутке (а; b).
Теорема2. Если функция f(x) определена и непрерывна на промежутке (а; b) и f ‘(x) всюду отрицательна (f ‘(x)< 0), тогда функция убывает на промежутке (а; b).
Пример1. Исследовать на монотонность у= 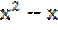 .
.
Решение: у’=2х-1
2х-1=0
х=0, 5
Числовая ось разбита на два интервала
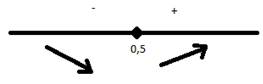
Значит, функция убывает в промежутке (-∞; 5) и функция возрастает в промежутке (5; ∞).
Нахождение экстремумов функции
Функция f(x) имеет максимум (минимум) в точке х0, если у этой точки существует окрестность, в которой f(x)< f(x0) (f(x)> f(x0)) для х≠ х0.
Максимум и минимум объединяются наименованием экстремум.
Теорема 1.(необходимое условие экстремума). Если точка х0 является точкой экстремума функции у=f(x) и в этой точке существует производная f ‘(x0), то она равна нулю: f ‘(x)=0.
Точки, где f ‘(x)=0 или не существует называются критическими.
Теорема 2.(достаточное условие). Пусть функция f(x) непрерывна в точке х0 и в ее δ – окрестности имеет производную, кроме, быть может, самой точки х0. Тогда
а) если производная f ‘(x) при переходе через точку х0 меняет знак с плюса на минус, то точка х0 является точкой максимума функции f(x);
б) если производная f ‘(x) при переходе через точку х0 меняет знак с минуса на плюс, то точка х0 является точкой минимума функции f(x);
в) если существует окрестность (х0-δ; х0+δ) точки х0, в которой производная f ‘(x) сохраняет свой знак, то в точке х0 данная функция f(x) не имеет экстремума.
Пример 2. Исследовать на экстремум функции у = 3 -5х - 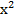 .
.
Решение: у’= -5-2x
-5-2х=0
-2х=5
х= - 2, 5

При переходе через точку х= - 2, 5 производная у’ меняет знак с «+» на «-» ==> х = -2, 5 точка максимума. xmax= - 2, 5; уmax = 9, 25.