
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания подготовлены кафедрой
|
|
общей физики
Издание переработанное и дополненное
Новосибирский государственный
технический университет, 2003г.
1. ВВЕДЕНИЕ
Термодинамика и молекулярная физика, которым посвящена данная работа, изучают одни и те же макроскопические процессы в телах, закономерности которых связаны с колоссальным количеством содержащихся в этих телах атомов и молекул. Взаимно дополняя друг друга, эти разделы физики отличаются различным подходом к изучаемым явлениям.
Выводы термодинамики основаны на общих принципах или началах, являющихся обобщением опытных фактов. При этом не вводится никаких гипотез о строении вещества.
Молекулярная физика, напротив, исходит из представления об атомно-молекулярном строении вещества и рассматривает теплоту как беспорядочное движение атомов и молекул.
Термодинамика изучает только равновесные состояния тел и общие закономерности перехода к таким состояниям, а так же равновесные процессы, которые могут рассматриваться как совокупности равновесных состояний, непрерывно следующих друг за другом.
Молекулярная физика изучает не только термодинамически равновесные состояния тел, (статистическая термодинамика), но и процессы в телах, идущие с конечными скоростями (физическая кинетика).
Достоинством термодинамики является то, что ее выводы характеризуются большой общностью, так как при их получении не используются упрощенные идеализированные молекулярные модели тел, без которых не может обойтись молекулярная физика. Однако последняя позволяет решать вопросы, теоретическое рассмотрение которых невозможно методами одной термодинамики: вывод уравнений состояния вещества, самопроизвольные нарушения состояния термодинамического равновесия (флуктуации) и др. Молекулярная физика устанавливает границы применимости термодинамики.
Следует отметить, что молекулярная физика должна основываться на законах, которым подчиняются атомы и молекулы. Эти законы изучаются позднее в разделе " Квантовая механика". Без знания этих законов строгое изложение современной молекулярной физики невозможно. Однако широкий круг макроскопических явлений обусловлен не столько деталями строения атомов и характером управляющих ими законов, сколько необычайно большим числом атомов в макроскопических системах. Такие явления и рассматриваются в данных методических указаниях.
2. ВОПРОСЫ, ВЫНОСИМЫЕ НА ЭКЗАМЕН ПО РАЗДЕЛУ " МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА"
1. Параметры состояния. Равновесное состояние, равновесные процессы.
2. Внутренняя энергия системы. Теплота. Работа, совершаемая телом при изменении объема.
3. Первое начало термодинамики.
4. Основное уравнение молекулярно-кинетической теории идеального газа.
5. Уравнение состояния идеального газа.
6. Молекулярно-кинетический смысл температуры.
7. Число степеней свободы. Закон равномерного распределения энергии по степеням свободы молекулы.
8. Внутренняя энергия и теплоемкость идеального газа.
9. Изотермический процесс. Уравнение состояния идеального газа, первое начало термодинамики, теплоемкость, работа, графики процесса.
10. Изохорический процесс. Уравнение состояния идеального газа, первое начало термодинамики, теплоемкость, работа, графики процесса.
11. Изобарический процесс. Уравнение состояния идеального газа, первое начало термодинамики, теплоемкость, работа, графики процесса.
12. Адиабатический процесс. Уравнение состояния идеального газа, первое начало термодинамики, теплоемкость, работа, графики процесса.
13. Закон распределения молекул газа по скоростям (распределение Максвелла).
14. Средние скорости теплового движения молекул газа.
15. Закон распределения молекул по значениям потенциальной (распределение Больцмана) и полной энергии (распределение Максвелла-Больцмана).
16. Энтропия. Второе начало термодинамики.
17. Цикл Карно, КПД цикла. Теорема Карно.
Список литературы
1. Савельев И. В. Курс общей физики. - М.: Наука, 1989. - T. I. (и более поздние издания).
2. Яворский Б. М., Детлаф А. А. Справочник по физике. - М.: Наука, 1985. (и более поздние издания).
3. Трофимова Т. И. Курс физики. - М.: Высшая школа, 1985. (и более поздние издания).
4. Матвеев А. Н. Молекулярная физика. - М.: Высшая школа, 1981.
5. Фен Дж. Машины, энергия, энтропия. - М.: Мир, 1986.
6. Сивухин Д. В. Общий курс физики. - М.: Наука, 1975. - Т. 2 (и более поздние издания).
3. СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ № 2
3.1. Молярная масса. Масса молекулы. Число молекул. Задачи № 201-210.
3.2. Уравнение состояния идеального газа. Задачи №211-220.
3.3. Энергия молекул, их скорость. Задачи № 221-230.
3.4. Первое начало термодинамики. Задачи № 231-240.
3.5. Теплоемкость. Задачи № 241-250.
3.6. Распределение молекул по скоростям. Средние скорости молекул. Задачи № 251-260.
3.7. Второе начало термодинамики. Энтропия. Задачи № 261-270.
3.8. Циклы тепловых машин. Задачи № 271-280.
4. КРАТКОЕ ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
4.1. Молярная масса. Масса молекулы. Число молекул
Молекулой называется устойчивая наименьшая частица вещества, обладающая его химическими свойствами. Молекула состоит из атомов, атом - из атомного ядра и электронной оболочки. В случае одноатомных молекул (например, у инертных газов) понятия молекулы и атома совпадают.
За атомную единицу массы принята 1/12 массы атома углерода изотопа С 12: 1 а.е.м. = 1, 66·10-27 кг (атомная единица массы - внесистемная единица измерения).
Относительной массой молекулы называется число, показывающее во сколько раз масса данной молекулы больше 1/12 массы атома углерода изотопа С 12. Обозначается буквой М.
Относительную массу молекулы М можно определить по таблице Менделеева и химической формуле молекулы. В таблице Менделеева даны массы атомов в атомных единицах (углеродных) с учетом изотопного состава природного элемента. Например, для молекулы водорода 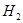 относительная масса молекулы М = 1´ 2 = 2 а.е.м. Масса молекулы в килограммах определяется умножением относительной массы молекулы на величину 1, 66·10-27 кг. Например, молекула воды (H 2 O) имеет массу (1´ 2 + 16 = 18 а.е.м. = 18´ 1, 66·1027 кг).
относительная масса молекулы М = 1´ 2 = 2 а.е.м. Масса молекулы в килограммах определяется умножением относительной массы молекулы на величину 1, 66·10-27 кг. Например, молекула воды (H 2 O) имеет массу (1´ 2 + 16 = 18 а.е.м. = 18´ 1, 66·1027 кг).
Молярной массой называется величина, численно равная массе одного моля (киломоля) молекул. Обозначается буквой μ (мю). Имеет размерность [ μ ]= κ г / моль.
Численное значение молярной массы в указанных единицах равно 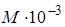 кг / моль, где М - относительная молекулярная масса.
кг / моль, где М - относительная молекулярная масса.
Моль - седьмая основная единица в системе единиц СИ. Это такое количество вещества, которое содержит столько же частиц (атомов или молекул), сколько их в 0, 012 кг углерода изотопа С 12.
Число молекул в моле называется числом Авогадро.
N A = 6, 02·1023 моль -1.
Молярная масса μ, масса молекулы 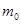 и число Авогадро
и число Авогадро  связаны соотношением
связаны соотношением
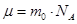 .
.
Концентрация молекул величина, равная отношению количества молекул в объеме V к величине этого объема. Обозначается буквой n.
n = N / V, [ n ] = м -3.
Плотность вещества 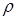 , равная отношению массы объема V к величине этого объема, может быть определена так
, равная отношению массы объема V к величине этого объема, может быть определена так
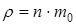 , [
, [ 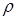 ] = кг / м 3,
] = кг / м 3,
где n - концентрация молекул; m 0 - масса одной молекулы.
Отношение массы вещества 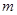 к его молярной массе дает количествовещества, т.е. число молей
к его молярной массе дает количествовещества, т.е. число молей
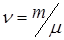 .
.
Число молей, умноженное на число Авогадро, дает общее число частиц в системе 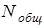 :
:
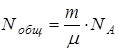 .
.
Общее число частиц, деленное на объем системы, определяет число частиц в единице объема, т.е. концентрацию частиц
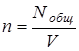 .
.
4.2. Уравнение состояния идеального газа
Опыт показывает, что в изолированных системах (в системах тел, которые не могут обмениваться энергией с окружающими объектами), каково бы ни было начальное состояние, в конце концов, устанавливается состояние термодинамического равновесия. Например, если в жесткой теплоизолированной оболочке привести в соприкосновение нагретый металл и холодную воду, то одно тело будет нагреваться, а другое охлаждаться, пока не прекратятся всякие макроскопические изменения. При этом полученное равновесное состояние с молекулярной точки зрения характеризуется интенсивным движением молекул и обменом энергией между частями изолированной системы, причем количество отдаваемой и принимаемой энергии для каждой части системы одинаково.
Состояние сложной системы, описанное настолько подробно, что учитываются состояние каждой частицы, называется микросостоянием. Однако если вспомнить про огромное количество частиц, составляющих тело, то ясно, что такое описание полезно лишь постольку, поскольку оно может быть использовано для определения макроскопических свойств системы.
Равновесное состояние, описанное с помощью параметров, которые относятся ко всему телу в целом, называется макросостоянием. Такими параметрами являются, например, давление, плотность, температура, концентрация частиц, объем и т.д.
С точки зрения молекулярной физики, ввиду теплового движения частиц, численные значения параметров макросостояния не могут оставаться строго постоянными с течением времени. Такие беспорядочные самопроизвольные отклонения параметров от своих средних значений называются флуктуациями. Можно показать, что роль флуктуаций уменьшается при увеличении числа частиц, составляющих систему.
Дадим определения некоторых параметров макросостояния.
Давлением называется величина, равная отношению силы F, которая действует на поверхность S в перпендикулярном к ней направлении, к площади этой поверхности
Р = F / S.
Давление газа на стенку сосуда является результатом ударов о стенку его молекул. Если газ является смесью нескольких компонентов, то общее давление смеси равно сумме парциальных давлений каждого из n газов:
Р смеси = Р 1+ Р 2+...+ Р n (Закон Дальтона).
Под объемом газа V понимается объем той области пространства, в которой могут перемещаться молекулы данного газа. Если собственным объемом молекул газа можно пренебречь по сравнению с объемом, в котором перемещаются молекулы, то объем газа будет равен объему сосуда, в котором газ находится. При этом если газ представляет собой смесь, то объем каждого компонента одинаков и равен объему сосуда:
 .
.
Физический смысл понятия термодинамической температуры Т для газов, молекулы которых подчиняются законам классической физики, был выяснен молекулярно-кинетической теорией, где показано, что температура – мера средней энергии молекул системы, находящейся в состоянии теплового равновесия. Под тепловым равновесием понимается частный случай термодинамического равновесия, при котором имеет место обмен энергией только за счет теплообмена (механического и химического энергообмена нет).
Опыт показывает, что в состоянии термодинамического равновесия, параметры состояния любой системы находятся в функциональной зависимости
f (P, V, T) = 0,
которая называется уравнением состояния тела.
Наиболее простой вид это уравнение имеет для идеальных газов
PV = ν RT (уравнение Менделеева-Клапейрона),
где R = 8, 3 Дж /(моль·К) - универсальная газовая постоянная.
4.3. Первое начало термодинамики
Первое начало термодинамики выражает принцип сохранения энергии для термодинамических процессов.
Любое тело, кроме кинетической энергии его макроскопического движения и потенциальной энергии во внешних силовых полях, обладает, в силу своего молекулярного строения, внутренней энергией. Внутренняя энергия U определяется как сумма кинетических энергий составляющих тело частиц (молекул, атомов, электронов и т.д.) и их потенциальной энергии в силовых полях, c помощью которых осуществляется взаимодействие между частицами. Энергия покоя частиц также является частью внутренней энергии тела.
Внутренняя энергия может изменяться, во-первых, за счет макроскопической работы при расширении (сжатии), во-вторых, за счет подведения (отведения) некоторого количества теплоты.
Можно показать, что в случае квазистатических (равновесных) процессов. т.е. процессов протекающих настолько медленно, что в каждый момент времени система находится практически в равновесном состоянии, макроскопическая элементарная работа газа равна
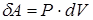 ,
,
где Р - постоянное давление; dV - малое приращение объема.
Работа для произвольного равновесного процесса определяется суммой элементарных работ
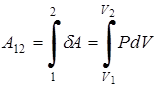 ,
,
где 1 – начальное, а 2 – конечное состояние системы.
Кроме совершения макроскопической работы, к изменению внутренней энергии тела может приводить теплообмен с окружающей средой. Энергия, переданная телу в результате теплообмена (теплопроводностью, конвекцией, излучением), называется количеством теплоты Q.
Из закона сохранения энергии следует, что количество подведенного к телу тепла может идти на приращение внутренней энергии тела и на совершение телом макроскопической работы над окружающими телами
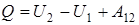 (первое начало термодинамики).
(первое начало термодинамики).
Здесь U 1 и U 2 - начальное и конечное значения внутренней энергии тела; A 12 - работа, совершенная телом (системой) при переходе от начального состояния к конечному; Q - количество сообщенной телу (системе) теплоты.
Первое начало термодинамики формулируется также следующим образом: невозможен перпетуум-мобиле (вечный двигатель) первого рода, т.е. такой периодически действующий двигатель, который совершал бы работу в бó льшем количестве, чем получаемая им извне энергия.
При вычислении работы и теплоты обычно приходится разбивать рассматриваемый процесс на ряд элементарных процессов, соответствующих очень малому (в пределе - бесконечно малому) изменению параметров состояния системы. Уравнение первого начала термодинамики для элементарного процесса имеет вид
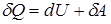 ,
,
где 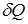 - элементарное количество теплоты;
- элементарное количество теплоты; 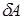 - элементарная работа; dU - приращение внутренней энергии системы в ходе данного элементарного процесса.
- элементарная работа; dU - приращение внутренней энергии системы в ходе данного элементарного процесса.
Внутренняя энергия системы представляет собой функцию состояния системы. Поэтому ее изменение при переходе системы из одного состояния в другое не зависит от пути, по которому совершался переход, и можно говорить о запасе внутренней энергии, которым обладает система в различных состояниях.
В отличие от внутренней энергии, количество теплоты 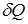 и работа
и работа 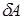 зависят от пути перехода из начального к конечному состоянию системы. Поэтому их называют функциями процесса и говорить о запасе теплоты и работы в системе бессмысленно.
зависят от пути перехода из начального к конечному состоянию системы. Поэтому их называют функциями процесса и говорить о запасе теплоты и работы в системе бессмысленно.
4.4. Закон равномерного распределения энергии по степеням свободы молекулы. Внутренняя энергия идеального газа. Скорости теплового движения молекул
Число независимых координат (чисел), однозначно определяющих положение механической системы в пространстве, называется числом степеней свободы этой системы. В классической теории атомы вещества рассматриваются как материальные точки. Поскольку для однозначного определения местоположения точки в пространстве относительно выбранного начала координат необходимо задать три координаты, например, x, y, z в декартовой системе координат, то считается, что одноатомная молекула имеет три степени свободы. Эти степени свободы называют поступательными, так как вращение материальной точки рассматривать бессмысленно. Примером газов, состоящих из одноатомных молекул, являются инертные газы.
Двухатомные молекулы при не очень высоких температурах (H 2, O 2, N 2 и др.) рассматриваются как совокупность двух жестко связанных материальных точек (гантель). Положение таких молекул в пространстве можно определить с помощью пяти чисел, три из которых определяют положение центра масс, а два - углы поворота " гантели" относительно осей координат. Следовательно, двухатомная молекула с жесткой связью между атомами имеет пять степеней свободы - три поступательные и две вращательные.
Трехатомные и многоатомные молекулы с жесткими связями (отсутствует колебательное движение атомов в молекуле относительно центра масс) имеют шесть степеней свободы - три поступательные и три вращательные.
При достаточно высокой температуре в молекулах состоящих из двух и более атомов возникает колебательное движение атомов относительно центра масс молекулы, т. е. появляются колебательные степени свободы.
Зная число степеней свободы молекулы и температуру газа, для вещества, находящегося в состоянии термодинамического равновесия, можно определить среднюю кинетическую энергию молекул этого газа с помощью закона равномерного распределения энергии по степеням свободы молекулы:
средняя энергия, приходящаяся на одну поступательную или вращательную степень свободы молекулы, равна 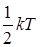 , а на каждую колебательную степень свободы приходится в два раза большая энергия. Здесь
, а на каждую колебательную степень свободы приходится в два раза большая энергия. Здесь 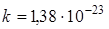 Дж/К - постоянная Больцмана.
Дж/К - постоянная Больцмана.
Используя этот закон, получим среднюю энергию одной молекулы
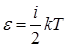 ,
,
где i - число степеней свободы молекулы:
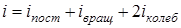 .
.
Поскольку для идеального газа потенциальной энергией взаимодействия молекул по сравнению с их кинетической энергией можно пренебречь, а энергия частиц, составляющих саму молекулу в процессах, которые рассматривает классическая термодинамика, не меняется, то можно считать внутреннюю энергию идеального газа равной сумме энергий поступательного, вращательного и колебательного движения его молекул:
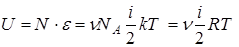 ,
,
где N - число молекул идеального газа, R – универсальная газовая постоянная.
Максвелл показал, что при равновесном состоянии газа существует определенное статистическое распределение молекул по скоростям:
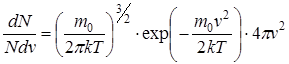 ,
,
где 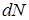 - количество молекул, скорости которых лежат в узком диапазоне от
- количество молекул, скорости которых лежат в узком диапазоне от 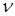 до
до 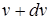 ;
;  - общее количество молекул газа;
- общее количество молекул газа; 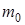 - масса одной молекулы;
- масса одной молекулы; 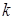 - постоянная Больцмана;
- постоянная Больцмана; 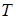 - абсолютная температура газа.
- абсолютная температура газа.
Пользуясь этим распределением, можно найти следующие средние скорости теплового движения молекул:
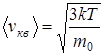 - средняя квадратичная скорость;
- средняя квадратичная скорость;
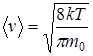 - средняя арифметическая скорость;
- средняя арифметическая скорость;
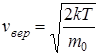 - наиболее вероятная скорость,
- наиболее вероятная скорость,
где m 0 - масса молекулы газа, Т - абсолютная температура.
При решении некоторых задач удобно перейти в распределении Максвелла к новой переменной, которую можно назвать относительной скоростью молекул:
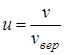 .
.
С этой переменной формула для распределения значительно упрощается:
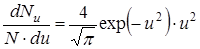 ,
,
где 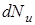 - количество молекул, относительные скорости которых лежат в узком диапазоне от
- количество молекул, относительные скорости которых лежат в узком диапазоне от 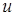 до
до 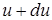 .
.
Используя эту формулу можно получить, например, долю молекул 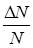 , относительные скорости которых лежат в пределах от
, относительные скорости которых лежат в пределах от 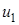 до
до 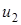 :
:
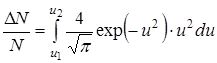 .
.
Если диапазон скоростей 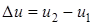 можно считать узким по сравнению с самой скоростью, то интегрирование в последней формуле можно не проводить и использовать формулу в виде
можно считать узким по сравнению с самой скоростью, то интегрирование в последней формуле можно не проводить и использовать формулу в виде
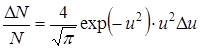 .
.
4.5. Теплоемкость
Теплоемкостью тела называют отношение бесконечно малого количества тепла 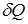 , подученного телом, к соответствующему приращению температуры dT
, подученного телом, к соответствующему приращению температуры dT
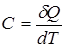 .
.
Отношение теплоемкости тела к его массе называется удельной теплоемкостью 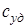 , а отношение к количеству вещества ν - молярной теплоемкостью с:
, а отношение к количеству вещества ν - молярной теплоемкостью с:
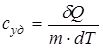 ,
, 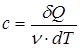 .
.
Очевидно, что
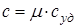 .
.
Важно отметить, что теплоемкость является функцией процесса. Для идеального газа можно получить выражения теплоемкостей через число степеней свободы молекулы при некоторых процессах
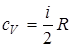 ,
, 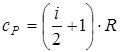 ,
,
где 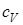 и
и 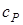 - молярные теплоемкости при постоянном объеме и давлении соответственно. Связь между ними имеет вид
- молярные теплоемкости при постоянном объеме и давлении соответственно. Связь между ними имеет вид
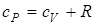 (уравнение Майера).
(уравнение Майера).
Для показателя адиабаты, который равен отношению теплоемкостей, получим
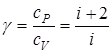 .
.
4.6. Первое начало термодинамики для изопроцессов
Рассмотрим часто встречающиеся в задачах термодинамики равновесные
процессы.
1. При изохорическом процессе объем не изменяется (V = const). То есть dV =0, вследствие чего работа 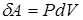 равна нулю. Это справедливо не только для идеального газа, но и вообще для всякого тела.
равна нулю. Это справедливо не только для идеального газа, но и вообще для всякого тела.
Первое начало термодинамики для этого процесса запишется
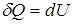 .
.
Читается так: вся подводимая к системе теплота расходуется на приращение ее внутренней энергии.
Из этого равенства следует, что теплоемкость тела при постоянном объеме равна
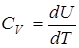 .
.
2. При изобарическом процессе (Р = const) работа газа равна
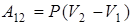 .
.
Первое начало термодинамики запишется так:
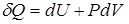 .
.
3. При изотермическом процессе (Т = const.) dT = 0. Тогда для идеального газа
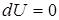 ,
,
так как его внутренняя энергия зависит только от температуры.
Первое начало термодинамики для этого процесса запишется так:
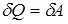 .
.
Подводимое тепло расходуется на совершение работы газом над внешними телами.
Получим выражение для работы при изотермическом процессе. Для этого, предварительно выразив давление из уравнения Менделеева-Клапейрона, подставим его в формулу для работы
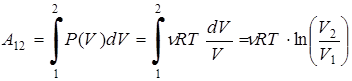 .
.
4. При адиабатическом процессе тепло не подводится к системе и не отводится, поэтому 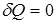 (нет теплообмена с внешней средой).
(нет теплообмена с внешней средой).
Первое начало термодинамики запишется
 ,
,
т.е. работа совершается газом за счет убыли его внутренней энергии.
Приращение внутренней энергии идеального газа можно выразить через теплоемкость и приращение температуры
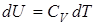 .
.
Следовательно, работа при адиабатическом процессе равна
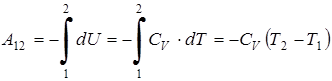 ,
,
где 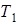 - начальная температура;
- начальная температура; 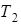 - конечная температура;
- конечная температура; 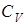 теплоемкость тела при V = const.
теплоемкость тела при V = const.
Уравнение состояния идеального газа для адиабатического процесса можно привести к виду
 (уравнение адиабаты).
(уравнение адиабаты).
Теплоемкость тела при постоянном объеме выражается через показатель адиабаты и универсальную газовую постоянную
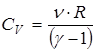 .
.
Используя эти соотношения, получаем еще одну формулу для работы при адиабатическом процессе
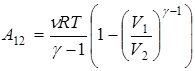 .
.
4.7. Второе начало термодинамики. Энтропия
В основе второго начала термодинамики лежат важные понятия термодинамической вероятности W и энтропии S.
Количество допустимых микросостояний, соответствующее данному макросостоянию (см. п.4.2.), называется термодинамической вероятностью (статистическим весом) этого макросостояния. Если, учитывая хаотичность движения молекул системы, принять гипотезу, что вероятность каждого микросостояния одинакова, то система, очевидно, бό льшую часть времени будет находиться в таком макросостоянии, которому соответствует бό льший статистический вес. Такие макросостояния системы называют беспорядочными, случайными. Состояния, осуществляемые относительно малым числом способов, называют упорядоченными или неслучайными. Предоставленная самой себе система, находящаяся в упорядоченном состоянии, за счет хаотичного движения молекул будет переходить самопроизвольно к все более беспорядочным макросостояниям, пока ни достигнет состояния с максимальным статистическим весом. В этом состоянии система будет находиться сколь угодном долго, если, конечно, исключить взаимодействие с внешними телами, причем время от времени будут обязательно наблюдаться случайные отклонения значений параметров макросостояния (флуктуации).
Использование самого статистического веса W в качестве характеристики макросостояния системы неудобно, так как эта величина не обладает свойством аддитивности: общий статистический вес системы равен не сумме, а произведению статистических весов ее частей, которые считаются независимыми друг от друга
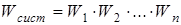 .
.
Иметь дело с аддитивными величинами удобней. Поэтому в качестве характеристики вероятности макросостояния принимается величина S, пропорциональная логарифму статистического веса
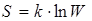 ,
,
которая называется энтропией. Здесь k - постоянная Больцмана.
Сказанное позволяет понять природу необратимых процессов и равновесных состояний системы.
Необратимым является такой процесс, обратный которому маловероятен. Таким образом, для необратимых процессов существует направление их самопроизвольного протекания: от малого статистического веса, т.е. малого значения энтропии к максимальному статистическому весу, а значит, - к максимальному значению энтропии.
Обратимым (равновесным, квазиравновесным) является процесс, который может протекать в двух направлениях, проходя при этом через одни и те же равновесные состояния. Причем, если процесс протекает сначала в одном направлении, а потом - в обратном, то система должна вернуться в исходное состояние без того, чтобы в окружающих телах произошли какие-либо изменения.
Равновесным является состояние с максимальным статистическим весом, т.е. с максимальной энтропией.
Из сказанного выше вытекают следующие свойства энтропии:
1. При протекании в изолированной системе необратимого процесса энтропия системы возрастает.
2. Энтропия системы, находящейся в равновесном состоянии, максимальна.
Утверждение о том, что энтропия изолированной системы не может убывать, называется законом возрастания энтропии и является одной из формулировок второго начала термодинамики.
Клаузиус сформулировал второе начало термодинамики следующим образом: невозможны такие процессы, единственным конечным результатом которых был бы переход некоторого количества теплоты от тела, мало нагретого к телу более нагретому.
Формулировка Томсона: невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от какого-то тела некоторого количества теплоты и превращение этой теплоты полностью в работу.
Еще одна формулировка - невозможен вечный двигатель второго рода, т.е. такой периодически действующий двигатель, который получал бы теплоту от одного резервуара, превращая ее полностью в работу.
Можно доказать, что все приведенные формулировки второго начала термодинамики являются равносильными.
Методами статистической физики показано, что для обратимого элементарного процесса приращение энтропии равно
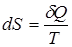 ,
,
где 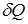 - количество теплоты, подведенное при постоянной температуре Т.
- количество теплоты, подведенное при постоянной температуре Т.
В случае равновесного адиабатического процесса 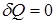 , тогда
, тогда 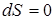 , следовательно, S = const.
, следовательно, S = const.
Для произвольного обратимого процесса 1-2
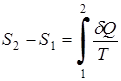 ,
,
где 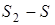 1 - приращение энтропии в процессе 1-2.
1 - приращение энтропии в процессе 1-2.
Для необратимого процесса
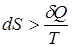 .
.
Замена равенства неравенством связана с тем, что энтропия возрастает при необратимом процессе, как за счет подводимого тепла, так и вследствие необратимости процесса.
4.8. Циклы тепловых машин. Цикл Карно
Тепловой машиной называют устройство, предназначенное для совершения полезной работы за счет подведения тепла. Для получения любого количества работы необходимо, чтобы тепловая машина работала циклически, возвращаясь после каждого цикла в исходное состояние.
Эффективность любой тепловой машины принято характеризовать коэффициентом полезного действия, который определяется как отношение совершаемой за цикл работы 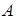 к получаемому от нагревателя за цикл количеству теплоты
к получаемому от нагревателя за цикл количеству теплоты 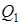 :
:
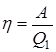 .
.
Так как изменение внутренней энергии любого рабочего вещества тепловой машины за цикл равно нулю (внутренняя энергия - функция состояния), то из первого начала термодинамики следует
 ,
,
где 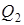 - количество теплоты, которое отдает тело холодильнику (например, окружающей среде).
- количество теплоты, которое отдает тело холодильнику (например, окружающей среде).
Следовательно,
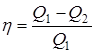 .
.
Карно доказал, что КПД любой тепловой машины, работающей при температуре нагревателя 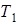 и холодильника
и холодильника 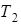 , не может превысить КПД обратимой тепловой машины. Причем у последней он определяется только температурами нагревателя
, не может превысить КПД обратимой тепловой машины. Причем у последней он определяется только температурами нагревателя 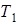 и холодильника
и холодильника 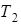 и не зависит от свойств рабочего вещества и устройства машины
и не зависит от свойств рабочего вещества и устройства машины
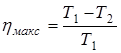 .
.
Задача. Определите плотность воздуха при давлении 830 мм.рт.ст. и температуре 17° С.
Дано:
“СИ”
P = 830 мм.рт.ст.

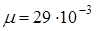 к г/моль к г/моль
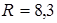 Дж /(К·моль) Дж /(К·моль)
| P = 830·133, 3 Н / м 2
Т = 290 К
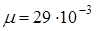 кг/моль кг/моль
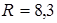 Дж /(К·моль) Дж /(К·моль)
|
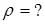
|
В условии задачи даны давление и температура. Кроме того, речь идет о конкретном газе - о воздухе, значит, мы можем найти в справочнике и записать его молярную массу 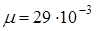 кг/моль. Понадобится универсальная газовая постоянная
кг/моль. Понадобится универсальная газовая постоянная 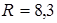 Дж /(К·моль) Указанный выше коэффициент, переводящий единицы давления в " СИ" 1 мм рт.ст. = 133, 3 Н / м 2, может быть получен с помощью известной формулы для давления жидкости на глубине h и взятой из справочника плотности ртути
Дж /(К·моль) Указанный выше коэффициент, переводящий единицы давления в " СИ" 1 мм рт.ст. = 133, 3 Н / м 2, может быть получен с помощью известной формулы для давления жидкости на глубине h и взятой из справочника плотности ртути 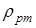 :
:
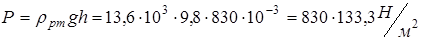 .
.
Решение. Плотностью называется физическая величина, равная отношению массы газа m к его объему V
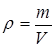 .
.
Из уравнения Клапейрона-Менделеева PV = ν RT выразим отношение m / V
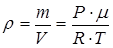 .
.
Проверим единицы измерения
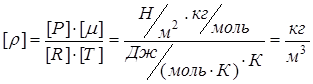 .
.
Найдем численное значение
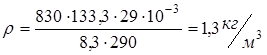 .
.
Ответ: 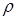 = 1, 3 кг / м 3.
= 1, 3 кг / м 3.
Задача. При свободном расширении некоторой массы идеального двухатомного газа была получена линейная зависимость объема от температуры: 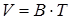 , где постоянный коэффициент
, где постоянный коэффициент 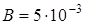 м 3/ К. Определите теплоемкость газа при постоянном давлении С р, изменение внутренней энергии газа
м 3/ К. Определите теплоемкость газа при постоянном давлении С р, изменение внутренней энергии газа 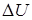 , совершенную им работу А и теплоту Q, переданную газу при его нагревании на
, совершенную им работу А и теплоту Q, переданную газу при его нагревании на 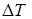 = 40 К при давлении
= 40 К при давлении 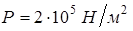 .
.
Дано:
i = 5 (двухатомный)
Δ T = 40 К
Р = 2· 105 Н / м 2
R = 8, 3 Дж /(моль· К)
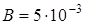 м 3/ К м 3/ К
|
| C P -? Δ U -? Q -? A -? |
Решение. Из условия свободного расширения газа можно заключить, что процесс, рассматриваемый в задаче, является изобарическим (Р = const). Искомые величины будем определять по формулам:
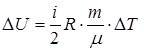 ;
;
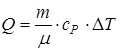 ;
;
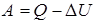 ;
;
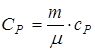 ,
,
где 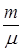 - число молей.
- число молей.
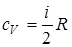 - молярная теплоемкость при постоянном объеме;
- молярная теплоемкость при постоянном объеме;
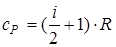 - молярная теплоемкость при постоянном давлении.
- молярная теплоемкость при постоянном давлении.
Величину 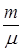 можно определить по заданной в условии задачи зависимости объема от температуры. Действительно, воспользуемся уравнением Клапейрона-Менделеева
можно определить по заданной в условии задачи зависимости объема от температуры. Действительно, воспользуемся уравнением Клапейрона-Менделеева
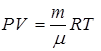 , отсюда
, отсюда 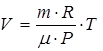 .
.
Сравнивая последнее выражение с зависимостью объема от температуры, заданной в условии задачи, видим, что 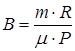 . Следовательно, количество молей газа равно
. Следовательно, количество молей газа равно 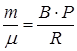 .
.
Теперь можно получить решение в общем виде:
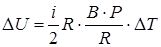 ;
;
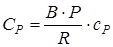 ;
;
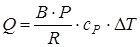 ;
;
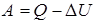 .
.
Проведя необходимые сокращения в полученных формулах, получаем численные значения искомых величин:
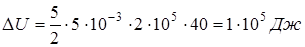 ;
;
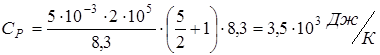 ;
;
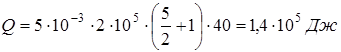 ;
;
 .
.
Ответ: 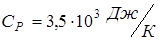 ;
; 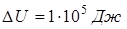 ;
; 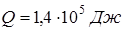 ;
; 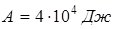 .
.
Задача. Найти изменение энтропии 280 г азота при изотермическом увеличении объема в 5 раз.
Дано:
| m = 280 г = 28· 10-2 кг μ = 28· 10-3 кг / моль R = 8, 3 Дж /(моль· К) |
| Δ S -? |
Решение. Из первого начала термодинамики:
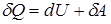 ,
,
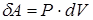 ,
,
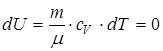 , т.к.
, т.к. 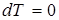 .
.
Выражение для работы преобразуем, считая азот идеальным газом
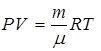 , откуда
, откуда 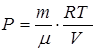 ;
;
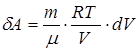 ,
, 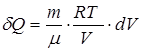 .
.
Для приращения энтропии получаем
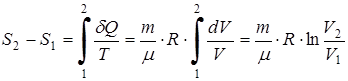 .
.
Проверяем единицы измерения
[ S ] = (кг· Дж· моль)/(кг· моль· К) = Дж / К.
Вычисляем
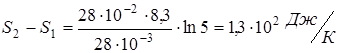 .
.
Ответ: Увеличение энтропии 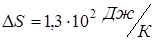 .
.
5. ТАБЛИЦА ВАРИАНТОВ ЗАДАЧ
| Вариант | Номера задач | |||||||
6. ЗАДАЧИ
201. Какова масса водорода в 1, 0 л воды?
202. Какое количество молекул газа находится в колбе емкостью V = 0, 50 л при нормальных условиях?
203. Определите концентрацию n молекул кислорода, находящегося в сосуде вместимостью V = 3 л. Количество вещества ν кислорода равно 0, 5 моль.
204. Сравните количество атомов в ν =0, 5 моль и в m = 0, 50 г кальция.
205. Сравните массы молекул кислорода и водорода.
206. Определите количество молей водорода, заполняющего сосуд объемом V = 3 л, если концентрация молекул газа в нем n = 2, 0· 1018 м -3
207. Сколько атомов кислорода содержится в 9, 0 л воды?
208. Одна треть молекул азота массой m = 10 г распалась на атомы. Сколько всего частиц находится в газе?
209. В баллоне емкостью V = 3, 0 л содержится кислород m = 10 г. Определите концентрацию молекул газа n.
210. Сколько атомов водорода содержится в 5, 0 молях воды?
211. Два сосуда одинакового объема содержат кислород. В одном сосуде давление P 1 = 1, 8 МПа, температура T 1 = 750 К, в другом Р 2 = 2, 0 МПа, T 2 = 250 К. Сосуды соединили трубкой и охладили находящийся в них кислород до температуры Т = 280 К. Определите установившееся в сосудах давление Р.
212. Азот находится в баллоне при температуре Т = 450 К. На сколько изменится плотность ρ азота при изменении давления на Δ Р = 1, 5 МПа и неизменной температуре Т = Const.
213. В сосуде вместимостью V = 30 л находится азот при температуре Т =273 К. Когда часть газа израсходовали, давление в сосуде понизилось на Δ Р =80 кПа. Определите массу m израсходованного газа. Процесс считать изотермическим.
214. Во сколько раз изменится плотность ρ кислорода при увеличении давления Р 1 = 2, 4 МПа до давления P 2 = 3, 6 МПа при постоянной температуре?
215. Определите массу m кислорода в баллоне вместимостью V = 10 л при температуре 27° С и давлении Р = 100 кПа.
216. В баллоне вместимостью V = 22 л находится азот при температуре Т =380 К. Когда часть газа израсходовали, давление в сосуде понизилось на Δ Р =180 кПа. Определите массу m израсходованного газа. Процесс считать изотермическим.
217. Определите массу газа в баллоне емкостью 30 л при температуре 22° С и давлении 5, 0· 105 Па, если его плотность при нормальных условиях - 1, 3 кг / м 3.
218. Баллон объемом V = 20 л заполнен аргоном при температуре Т = 360 К. На сколько изменится давление в баллоне при медленной утечке m =50 г газа?
219. Найти плотность газовой смеси водорода и кислорода, если их массовые доли соответственно 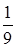 и
и 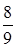 . Давление смеси равно Р =100 кПа, температура Т = 300 К.
. Давление смеси равно Р =100 кПа, температура Т = 300 К.
220. В сосуде объемом V = 15 л находится смесь азота и кислорода при 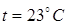 и давлении Р = 200 кПа. Определите массу m смеси, если массовая доля азота в смеси равна 0, 7.
и давлении Р = 200 кПа. Определите массу m смеси, если массовая доля азота в смеси равна 0, 7.
221. Определите внутреннюю энергию водорода, а также кинетическую энергию молекулы этого газа при температуре t= 27° С, если количество вещества водорода ν = 0, 5 моль.
222. В сосуде объемом V = 2, 0 л находится газ под давлением Р = 0, 50 МПа. Определите суммарную кинетическую энергию Е к поступательного движения всех молекул этого газа.
223. Баллон емкостью V = 0, 05 м 3 содержит ν = 0, 12 кмоль газа при давлении Р = 6, 0 МПа. Найдите среднюю кинетическую энергию поступательного движения одной молекулы газа.
224. Аммиак находится при температуре t= 27° С. Определите кинетическую энергию, приходящуюся на одну степень свободы молекулы аммиака NH 3, кинетическую энергию < ω вращ> вращательного движения и полную кинетическую энергию молекулы.
225. Найдите суммарную кинетическую энергию теплового движения молекул, содержащихся в азоте массой 7, 0 г при температуре 16° С. Какая часть этой энергии приходится на долю вращательного движения?
226. Определите полную кинетическую энергию молекул кислорода при температуре t= 18° С, а также среднюю кинетическую энергию вращательного движения одной молекулы газа. Количество вещества кислорода ν = 1, 0 моль.
227. Найдите кинетическую энергию поступательного движения молекулы водяного пара, полную кинетическую энергию молекулы, а также внутреннюю энергию одного киломоля пара, находящегося при температуре Т = 600 К.
228. Суммарная кинетическая энергия всех молекул, содержащихся в одном моле азота, при некоторой температуре составляет 6, 2 кДж. Определите температуру газа и среднюю кинетическую энергию вращательного движения одной его молекулы.
229. Кислород массой m = 12 г находится при температуре t= 700° С, при этом 40% молекул диссоциировано на атомы. Определите полную кинетическую энергию теплового движения частиц.
230. Азот массой m = 2, 0 кг охлаждают от температуры Т 1 = 400 К до температуры Т 2 = 300 К. Определите изменение кинетической энергии всех молекул азота, а также изменение кинетической энергии вращательного движения одной его молекулы.
231. Кислород, занимавший при давлении Р 1 = 120 кПа объем V= 8, 0 л расширился вдвое. Определите конечное давление и работу, совершенную газом при изобарном и изотермическом процессах. Начертите графики процессов в координатах P, V.
232. Азот массой m = 35 г, имевший температуру Т = 295 К, адиабатически расширился, увеличившись в объеме в 3, 5 раза. Затем при изотермическом сжатии объем газа уменьшился в 2 раза. Определите полную работу газа и его конечную температуру.
233. Кислород массой 0, 15 кг был изобарически нагрет от Т 1 = 215 К до Т 2 = 400 К. Определите работу А 1совершенную газом, полученную теплоту Q и изменение внутренней энергии.
234. Азот массой m = 1, 8 кг охлаждают при постоянном давлении от Т 1 = 410 К до Т 2 = 295 К. Определите изменение внутренней энергии, работу и количество выделенной теплоты.
235. Определенная масса азота при давлении P 1 = 0, 20 МПа занимает объем V = 2, 1 л, а при давлении P 2 = 1, 0 МПа объем V = 4, 8 л. Найдите количество теплоты, сообщенное газу, изменение внутренней энергии и совершенную работу при переходе газа из первого состояния во второе сначала изобарно, затем изохорно.
236. Определите работу, совершенную кислородом при адиабатическом расширении от V 1 = 2, 0 л до V 2 = 10 л. Начальное давление было P 1 = 1, 4 МПа.
237. При нагревании азота в условиях постоянного давления ему было сообщено Q =21 кДж теплоты. Какую работу А совершил при этом газ? Как изменилась его внутренняя энергия?
238. Водород массой 250 г изотермически расширился в 2, 5 раза за счет полученной теплоты. Сколько теплоты Q получил газ, какую при этом работу А совершил? Температура газа Т = 320 К.
239. Определенная масса кислорода занимает объем V 1 = 2, 1 л при давлении P 1 = 0, 22 МПа, а при давлении P 2 = 1, 0 МПа занимает объем V 2 = 5, 0 л. Определите количество теплоты, сообщенное газу, изменение внутренней энергии и совершенную работу при переходе из первого состояния во второе сначала изохорно, затем изобарно.
240. Кислород массой т = 300 г имевший температуру Т 1 = 295 К был адиабатически сжат. При этом была совершена работа А = 30 кДж. Определите конечную температуру газа Т 2.
241. В сосуде объемом V = 150 л находится идеальный газ при температуре Т = 350 К и давлении Р = 0, 2 МПа. Найдите теплоемкость С V газа, если показатель адиабаты γ = 1, 4.
242. Определите теплоемкость С V двухатомного газа, который при температуре Т = 350 К и давлении Р = 0, 4 МПа занимает объем V = 3 л.
243. Определите показатель адиабаты γ идеального газа, который при температуре Т = 350 К и давлении Р = 0, 4 МПа занимает объем V = 300 л и имеет теплоемкость С V = 857 Дж/К.
244. Определите число степеней свободы молекулы газа, если его молярная теплоемкость с Р = 29, 05· 103 Дж /(кмoльּ K).
245. В сосуде вместимостью V = 6 л находится при нормальных условиях двухатомный газ. Определите теплоемкость этого газа при постоянном объеме С V.
246. Определите молярные теплоемкости газа, если его удельные теплоемкости при постоянном объеме и давлении равны с Vуд = 10, 4 кДж /(кг· К) и с Pуд = 14, 6 кДж /(кг· К).
247. Найдите удельные теплоемкости и показатель адиабаты одноатомного газа, зная, что его молярная масса μ = 20· 10 –3 кг / моль.
248. Вычислите удельные теплоемкости газа, зная, что его молярная масса μ = 4· 10-3 кг/моль и отношение теплоемкостей С р/ С V= 1, 67.
249. Трехатомный газ под давлением Р = 240 кПа и температуре t = 20° С занимает объем V = 10 л. Определите теплоемкость С р этого газа при постоянном давлении.
250. Одноатомный газ при нормальных условиях занимает объем V = 5 л. Вычислите теплоемкость С V этого газа при постоянном объеме.
251. Какая часть молекул сернистого ангидрида SO 2 при температуре 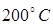 обладает скоростями в пределах 210-220 м/с; 420-430 м/с?
обладает скоростями в пределах 210-220 м/с; 420-430 м/с?
252. При какой температуре среднеквадратичная скорость молекул азота равна среднеарифметической скорости молекул водорода, находящихся при температуре Т = 400 К? Чему равна при этой температуре наиболее вероятная скорость молекул водорода и азота?
253. Считая, что сухой воздух состоит из 78% азота, 21% кислорода и 1% аргона (по объему), определите, какая часть молекул от общего числа при температуре 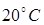 движется со скоростями от 350 до 360 м/с.
движется со скоростями от 350 до 360 м/с.
254. Какая часть молекул азота, находящегося при температуре Т, имеет скорости, лежащие в интервале от наиболее вероятной скорости 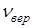 до
до 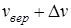 , где
, где 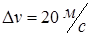 ? Задачу решите для Т 1 = 400 К и Т 2 = 900 К.
? Задачу решите для Т 1 = 400 К и Т 2 = 900 К.
255. Найдите среднеквадратичную, наиболее вероятную и среднеарифметическую скорости молекул метана (CH 4) при 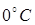 .
.
256. Найдите отношение среднеквадратичной, наиболее вероятной и среднеарифметической скорости молекул кислорода к скорости пылинок, находящихся среди молекул кислорода (масса одной пылинки равна 10–8 г).
257. Найдите число молекул азота, заключающихся при нормальных условиях в 1 см 3 и обладающих скоростью: а) между 99 и 101 м/с, б) между 499 и 501 м/с. Плотность азота при нормальных условиях равна 1, 25 кг/м 3.
258. Какой процент молекул обладает скоростями, разнящимися от наиболее вероятной не более чем на 1%?
259. Найдите отношение числа молекул водорода, скорости которых лежат в пределах от 299 до 301 м/с к числу молекул, имеющих скорости в пределах от 149 до 151 м/с, если температура водорода 300 К.
260. При какой температуре число молекул азота, обладающих скоростями в интервале от 299 до 301 м/с, равно числу молекул, обладающих скоростями в интервале от 599 до 601 м/с?
261. При изотермическом сжатии давление азота массой m = 2 кг было увеличено от Р 1 = 50 кПа до P 2 = 0, 5 МПа. Определите изменение энтропии газа.
262. Найдите изменение энтропии Δ S и количество теплоты Q, переданное азоту массой m = 4 г, находящемуся при нормальных условиях. В результате изобарического расширения объем газа изменяется от V 1 = 5 л до V 2 = 9 л.
263. Кислород массой m = 2 кг увеличил свой объем один раз - изотермически, другой - адиабатически. Каково будет изменение энтропии в этих двух случаях, если n = V 2/ V 1 = 5?
264. Водород массой m = 1 г находится при нормальных условиях. При изохорическом нагревании давление Р газа увеличилось в два раза. Определите изменение энтропии и переданное ему количество теплоты.
265. Водород массой m = 100 г был изобарически нагрет так, что объем его увеличился в n раз, затем водород был изохорически охлажден так, что давление его уменьшилось в n раз. Найдите изменение энтропии, если n = 3.
266. Азот массой m = 0, 1 кг был изобарно нагрет от температуры T 1 = 200 К до температуры Т 2 = 400 К. Найдите изменение Δ S энтропии и работу А, совершенную газом.
267. Объем водорода при изотермическом расширении при температуре Т =300 К увеличился в n = 3 раза. Определите работу А, совершенную газом, теплоту Q, полученную при этом, и изменение Δ S энтропии. Масса m водорода равна 200 г.
268. Найдите изменение Δ S энтропии и количество теплоты Q, которое надо сообщить кислороду, находящемуся в баллоне емкостью V = 50 л при нормальных условиях, если при изохорном нагревании давление газа. повысилось на Δ Р = 0, 5 МПа.
269. Смешано m 1 = 5 кг воды при температуре Т 1 = 280 К с m 2 = 8 кг воды при температуре T 2 = 350 К. Найдите: 1) температуру смеси; 2) изменение Δ S энтропии, происходящее при смешивании. Удельная теплоемкость воды С уд = 4, 2 кДж / (кг· К).
270. Кусок льда массой m = 200 г, взятый при температуре t 1 = -10° С, был нагрет до t 2 = 0° С и расплавлен, после чего образовавшаяся вода была нагрета до температуры t 3 = 10° C. Определите изменение Δ S энтропии льда. Удельная теплоемкость льда с л =2, 1 кДж /(кг· К), воды с в = 4, 2· 103 Дж /(кг· K), удельная теплота плавления льда λ = 3, 36· 105 Дж / кг.
271. Тепловая машина, работающая по циклу Карно, имеет температуру нагревателя Т 1 = 450 К. Отдавая охладителю теплоту Q 2 = 14 кДж, за один цикл машина совершает работу А = 6 кДж. Найдите температуру охладителя Т 2.
272. Газ, совершающий цикл Карно, получил от нагревателя теплоту Q 1 = 5, 6 кДж и за один цикл совершил работу А = 2, 2 кДж. Определите температуру охладителя, если температура нагревателя Т 1 = 500 К.
273. Идеальная тепловая машина работает по циклу Карно. Температура нагревателя Т 1 = 450 К, температура охладителя Т 2 = 270 К. Определите КПД цикла, а также работу А 1, совершенную при изотермическом расширении, если при изотермическом сжатии совершена работа А 2 = 60 Дж.
274. Идеальный о
|