по курсу

" Математическая статистика 2"

Выполнил студент группы 351 з шифр______ Адрес: ______

Принял:

профессор каф. ПМ

Федоров А.В..

Задание 1 и 2. Имеются n опытов наблюдения случайных величин X и Y. Сгладить зависимость имеющегося статистического материала 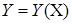с помощью метода наименьших квадратов (МНК).

1. Линейной функцие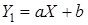й , и

2. Квадратичной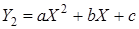

В плоскости 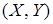нанести точки статистического материала и соответствующие функции.

Решение 1:

Для нахождения оценок a и b линейной функции МНК применим метод максимального правдоподобия.

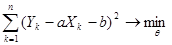
Распишем сумму квадратов:

.

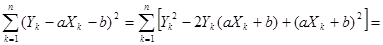
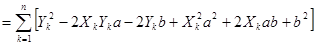Введем обозначения:

, , , ,

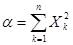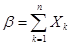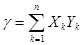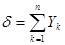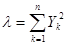
С учетом этих обозначений получаем, что функция ошибки, которую следует минимизировать, равна:

J (a, b) = a a ² + nb ² + 2 b ab – 2 g a – 2 d b + l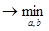

Находим частные производные и приравниваем нулю:

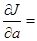2 a a + 2 b b – 2 g,

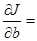2 nb + 2 b a – 2 d.

Для определения параметров искомой функции решаем систему:

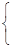
	a a + b b = g,
nb + b a = d.

Получаем для a, b:

,

.

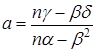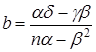Таблица параметров линейной корреляции.

	i=1	i=2	i=3	i=4	i=5

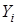
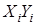
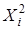
Смотри также https://www.cleverstudents.ru/articles/mnk.html

Решение 2:

Оценки параметров можно получить, решая так называемую нормальную систему уравнений:

,

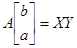где , ,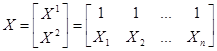

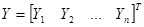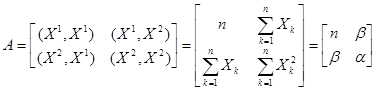
Получаем:

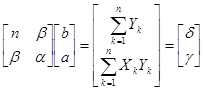
т.е. то же самое в виде системы:

	nb + b a = d.
a a + b b = g,

Как видно, это та же система, что и в решении 1.

Таким образом, с учетом данных, полученных в опытах по наблюдению за X и Y, получаем значения коэффициентов:

a = 46, 5000961858679,

b = 46, 1733376283488,

g = 147, 911922402037,

d = 146, 973081745395,

l = 471, 011023261011.

Получив значения коэффициентов, получаем значения оценки параметров:

a = 3, 15684427413119,

b = 0, 0242209047163106.

На рис. 2 представлена прямая .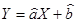

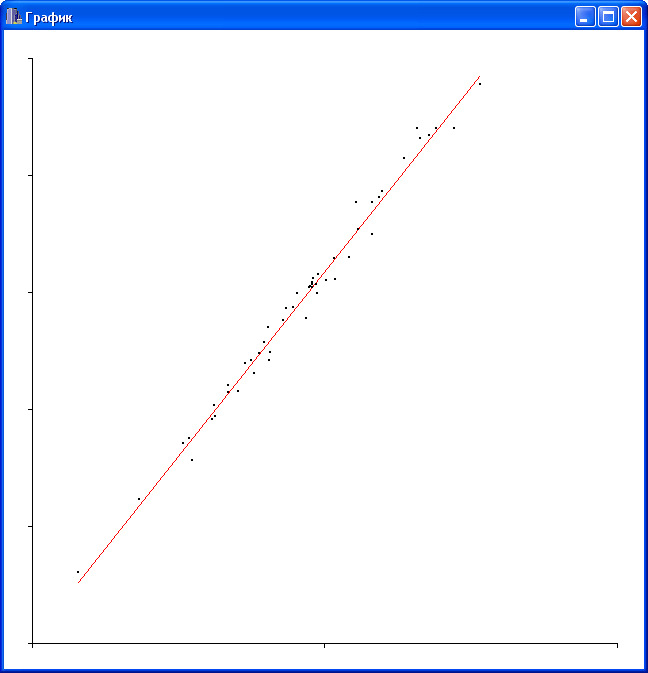
Рис. 2. Результаты оценки параметров.

Смотри также в книге Вентцель Елена Сергеевна. Теория вероятностей

М., 196. 576 стр. Пункт 14.8. Сглаживание экспериментальных зависимостей

по методу наименьших квадратов на стр. 351 теорию о сглаживании с помощью квадратичной функции Y= a X² + b X + с,