Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Циклическим процессом
|
|
Минимальным объектом в векторном графическом редакторе является… объект (прямоугольник, круг, линия и т.д.)
Минимальным объектом в растровом графическом редакторе является… точка экрана (пиксель)
Минимальным объектом, используемым в текстовом редакторе, является… символ (знакоместо)
Минимальным элементом растрового изображения является: п иксель
Моноширный шрифт – это шрифт: когда все символы имеют одинаковую ширину
Множество мощности 0 называется пустым
Мощность множества В больше мощности множества А. Тогда факт принадлежности всех элементов множества А множеству В представляют выражением 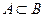
Математическое ожидание случайной величины Х равно 2, 4. Значение выражения 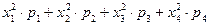 равно 8, 4. Тогда дисперсия случайной величины Х равна 2, 64
равно 8, 4. Тогда дисперсия случайной величины Х равна 2, 64
Математическое ожидание случайной величины Х равно 4, 9. Значение выражения 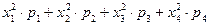 равно 24, 9. Тогда дисперсия случайной величины Х равна 0, 89
равно 24, 9. Тогда дисперсия случайной величины Х равна 0, 89
Математическое ожидание случайной величины Х равно 2, 1. Значение выражения 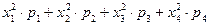 равно 5, 9. Тогда дисперсия случайной величины Х равна 1, 49
равно 5, 9. Тогда дисперсия случайной величины Х равна 1, 49
Математическое ожидание случайной величины Х равно 0, 8. Значение выражения 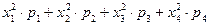 равно 2, 4. Тогда дисперсия случайной величины Х равна 1, 76
равно 2, 4. Тогда дисперсия случайной величины Х равна 1, 76
Математическое ожидание случайной величины Х равно 2, 8. Значение выражения 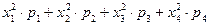 равно 9, 4. Тогда дисперсия случайной величины Х равна 1, 56
равно 9, 4. Тогда дисперсия случайной величины Х равна 1, 56
Математическое ожидание случайной величины Х равно 1, 5. Значение выражения 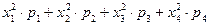 равно 5, 1. Тогда дисперсия случайной величины Х равна 2, 85
равно 5, 1. Тогда дисперсия случайной величины Х равна 2, 85
Математическое ожидание случайной величины Х равно –0, 4. Значение выражения 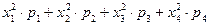 равно 2, 2. Тогда дисперсия случайной величины Х равна 2, 04
равно 2, 2. Тогда дисперсия случайной величины Х равна 2, 04
Математическое ожидание случайной величины Х равно 2, 4. Значение выражения 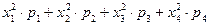 равно 7, 6. Тогда дисперсия случайной величины Х равна 1, 84
равно 7, 6. Тогда дисперсия случайной величины Х равна 1, 84
Математическое ожидание случайной величины Х равно –0, 3. Значение выражения 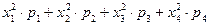 равно 0, 9. Тогда дисперсия случайной величины Х равна 0, 81
равно 0, 9. Тогда дисперсия случайной величины Х равна 0, 81
Математическое ожидание случайной величины Х равно 1, 2. Значение выражения 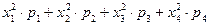 равно 3, 0. Тогда дисперсия случайной величины Х равна 1, 56
равно 3, 0. Тогда дисперсия случайной величины Х равна 1, 56
Математическое ожидание случайной величины Х равно 0, 33. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
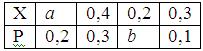
Тогда значения величин а и b равны: a = 0, 5; b = 0, 4
Математическое ожидание случайной величины Х равно 0, 33. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
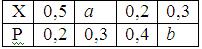
Тогда значения величин а и b равны: a = 0, 4; b = 0, 1
Математическое ожидание случайной величины Х равно 0, 41. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
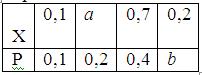
Тогда значения величины а и дисперсии равны: a = 0, 3; b = 0, 3
Математическое ожидание случайной величины Х равно 0, 41. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
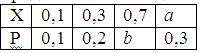
Тогда значения величины а и дисперсии равны: a = 0, 2; b = 0, 4
Математическое ожидание случайной величины Х равно 0, 23. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
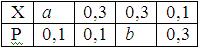
Тогда значения величины а и дисперсии равны: a = 0, 2; b = 0, 5
Математическое ожидание случайной величины Х равно 0, 23. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
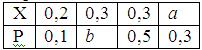
Тогда значения величины а и дисперсии равны: a = 0, 1; b = 0, 1
Математическое ожидание случайной величины Х равно 0, 21. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
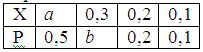
Тогда значения величины а и дисперсии равны: a = 0, 2; b = 0, 2
Математическое ожидание случайной величины Х равно 0, 21. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
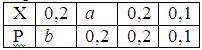
Тогда значения величины а и дисперсии равны: a = 0, 3; b = 0, 5
Математическое ожидание случайной величины Х равно 0, 22. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
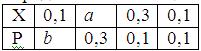
Тогда значения величины а и дисперсии равны: a = 0, 4; b = 0, 5
Математическое ожидание случайной величины Х равно 0, 22. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
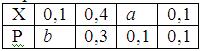
Тогда значения величины а и дисперсии равны: a = 0, 3; b = 0, 5
Математическое ожидание случайной величины Х равно 0, 33. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:

Тогда значения величины а и дисперсии равны: a =0, 5; D(X) =0, 0142
Математическое ожидание случайной величины Х равно 0, 33. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
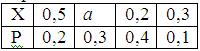
Тогда значения величины а и дисперсии равны: a =0, 4; D(X) =0, 0142
Математическое ожидание случайной величины Х равно 0, 41. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
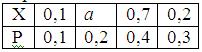
Тогда значения величины а и дисперсии равны: a =0, 3; D(X) =0, 0589
Математическое ожидание случайной величины Х равно 0, 41. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
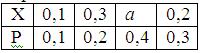
Тогда значения величины а и дисперсии равны: a =0, 7; D(X) =0, 0589
Математическое ожидание случайной величины Х равно 0, 23. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
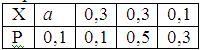
Тогда значения величины а и дисперсии равны: a =0, 2; D(X) =0, 0091
Математическое ожидание случайной величины Х равно 0, 23. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
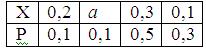
Тогда значения величины а и дисперсии равны: a =0, 3; D(X) =0, 0091
Математическое ожидание случайной величины Х равно 0, 21. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
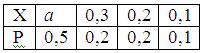
Тогда значения величины а и дисперсии равны: a =0, 2; D(X) =0, 0029
Математическое ожидание случайной величины Х равно 0, 21. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:

Тогда значения величины а и дисперсии равны: a =0, 3; D(X) =0, 0029
Математическое ожидание случайной величины Х равно 0, 22. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
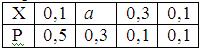
Тогда значения величины а и дисперсии равны: a =0, 4; D(X) =0, 0146
Математическое ожидание случайной величины Х равно 0, 22. Ряд распределения вероятностей случайной величины Х, с которыми Х принимает возможные значения, представлен таблицей:
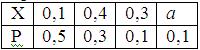
Тогда значения величины а и дисперсии равны: a =0, 1; D(X) =0, 0146
Мальчик действует по следующему алгоритму:
Шаг 1. Пройти 10 м прямо.
Шаг 2. Повернуть направо.
Шаг 3. Повторять шаги 1-2, пока не будет пройдено 80 м.
Шаг 4. Остановиться.
После выполнения шага 4 расстояние до точки, из которой мальчик начал свое движение, составит… 0
Мальчик действует по следующему алгоритму:
Шаг 1. Пройти 12 м прямо.
Шаг 2. Повернуть направо.
Шаг 3. Повторять шаги 1-2, пока не будет пройдено 84 м.
Шаг 4. Остановиться.
После выполнения шага 4 расстояние до точки, из которой мальчик начал свое движение, составит… 12
Мальчик действует по следующему алгоритму:
Шаг 1. Пройти 14 м прямо.
Шаг 2. Повернуть налево.
Шаг 3. Повторять шаги 1-2, пока не будет пройдено 56 м.
Шаг 4. Остановиться.
После выполнения шага 4 расстояние до точки, из которой мальчик начал свое движение, составит… 0
Мальчик действует по следующему алгоритму:
Шаг 1. Пройти 16 м прямо.
Шаг 2. Повернуть направо.
Шаг 3. Повторять шаги 1-2, пока не будет пройдено 80 м.
Шаг 4. Остановиться.
После выполнения шага 4 расстояние до точки, из которой мальчик начал свое движение, составит… 16
Мальчик действует по следующему алгоритму:
Шаг 1. Пройти 4 м прямо.
Шаг 2. Повернуть направо и пройти еще 3 м.
Шаг 3. Повторять шаги 1-2, пока не будет пройдено 28 м.
Шаг 4. Остановиться.
После выполнения шага 4 расстояние до точки, из которой мальчик начал свое движение, составит… 0
Мальчик действует по следующему алгоритму:
Шаг 1. Пройти 14 м прямо.
Шаг 2. Повернуть направо и пройти еще 2 м.
Шаг 3. Повторять шаги 1-2, пока не будет пройдено 78 м.
Шаг 4. Остановиться.
После выполнения шага 4 расстояние до точки, из которой мальчик начал свое движение, составит… 14
Мальчик действует по следующему алгоритму:
Шаг 1. Пройти 8 м прямо.
Шаг 2. Повернуть налево и пройти еще 3 м.
Шаг 3. Повторять шаги 1-2, пока не будет пройдено 52 м.
Шаг 4. Остановиться.
После выполнения шага 4 расстояние до точки, из которой мальчик начал свое движение, составит… 8
Мальчик действует по следующему алгоритму:
Шаг 1. Пройти 16 м прямо.
Шаг 2. Повернуть направо и пройти еще 5 м.
Шаг 3. Повторять шаги 1-2, пока не будет пройдено 84 м.
Шаг 4. Остановиться.
После выполнения шага 4 расстояние до точки, из которой мальчик начал свое движение, составит… 0
Мальчик действует по следующему алгоритму:
Шаг 1. Пройти 4 м прямо.
Шаг 2. Повернуть направо и пройти еще 4 м.
Шаг 3. Повторять шаги 1-2, пока не будет пройдено 36 м.
Шаг 4. Остановиться.
После выполнения шага 4 расстояние до точки, из которой мальчик начал свое движение, составит… 4
Мальчик действует по следующему алгоритму:
Шаг 1. Купить стакан сока за 20 руб.
Шаг 2. Выпить сок и подождать 1 час.
Шаг 3. Повторять шаги 1-2, пока не останется 10 руб.
Шаг 4. Пойти домой.
Если изначально у мальчика было 50 рублей, то домой он пойдет… через 2 часа
Мальчик действует по следующему алгоритму:
Шаг 1. Купить стакан сока за 14 руб.
Шаг 2. Выпить сок и подождать 1 час.
Шаг 3. Повторять шаги 1-2, пока не останется 2 руб.
Шаг 4. Пойти домой.
Если изначально у мальчика было 44 рублей, то домой он пойдет… через 3 часа
Мальчик действует по следующему алгоритму:
Шаг 1. Купить стакан сока за 16 руб.
Шаг 2. Выпить сок и подождать 1 час.
Шаг 3. Повторять шаги 1-2, пока не останется 4 руб.
Шаг 4. Пойти домой.
Если изначально у мальчика было 36 рублей, то домой он пойдет… через 2 часа
Мальчик действует по следующему алгоритму:
Шаг 1. Купить стакан сока за 24 руб.
Шаг 2. Выпить сок и подождать 1 час.
Шаг 3. Повторять шаги 1-2, пока не останется 4 руб.
Шаг 4. Пойти домой.
Если изначально у мальчика было 76 рублей, то домой он пойдет… через 3 часа
Мальчик действует по следующему алгоритму:
Шаг 1. Купить стакан сока за 15 руб.
Шаг 2. Выпить сок и подождать 1 час.
Шаг 3. Повторять шаги 1-2, пока не останется 3 руб.
Шаг 4. Пойти домой.
Если изначально у мальчика было 33 рублей, то домой он пойдет … через 2 часа
Множество мощности 0 называется пустым
Назначение отчетов в ACCESS: для подведения и распечатки итогов из таблиц или запросов.
Наиболее известными способами представления графической информации являются: векторный и растровый
Наиболее распространённое расширение в имени текстовых файлов *.txt
Непосредственное выполнение работы на компьютере пользователю обеспечивают прикладные программы
Несуществующая база данных: логические
Номер строки, которую будет занимать фамилия ИВАНОВ после проведения сортировки по возрастанию в поле ГОД РОЖДЕНИЯ 3
Непрерывная нормально распределенная случайная величина Х задана плотностью распределения вероятностей
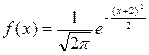 .
.
Тогда математическое ожидание случайной величины Х равно –2
Непрерывная нормально распределенная случайная величина Х задана плотностью распределения вероятностей
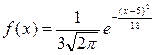 .
.
Тогда математическое ожидание случайной величины Х равно 5
Непрерывная нормально распределенная случайная величина Х задана плотностью распределения вероятностей
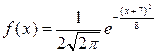 .
.
Тогда математическое ожидание случайной величины Х равно –7
Непрерывная нормально распределенная случайная величина Х задана плотностью распределения вероятностей
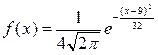 .
.
Тогда математическое ожидание случайной величины Х равно 9
Непрерывная нормально распределенная случайная величина Х задана плотностью распределения вероятностей
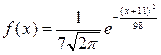 .
.
Тогда математическое ожидание случайной величины Х равно –11
Непрерывная нормально распределенная случайная величина Х задана плотностью распределения вероятностей
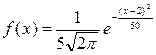 .
.
Тогда дисперсия случайной величины Х равна 25
Непрерывная нормально распределенная случайная величина Х задана плотностью распределения вероятностей
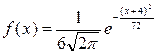 .
.
Тогда дисперсия случайной величины Х равна 36
Непрерывная нормально распределенная случайная величина Х задана плотностью распределения вероятностей
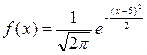 .
.
Тогда дисперсия случайной величины Х равна 1
Непрерывная нормально распределенная случайная величина Х задана плотностью распределения вероятностей
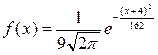 .
.
Тогда дисперсия случайной величины Х равна 81
Непрерывная нормально распределенная случайная величина Х задана плотностью распределения вероятностей
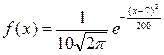 .
.
Тогда дисперсия случайной величины Х равна 100
Наиболее часто встречающееся значение признака в вариационном ряду называется мода
Наиболее наглядной формой описания алгоритма является представление алгоритма в виде схемы
Наиболее наглядным способом записи алгоритма является изображение в виде последовательно блоков, каждый из которых предписывает выполнение определенных действий
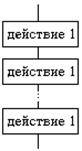
На блок-схеме изображена алгоритмическая структура типа
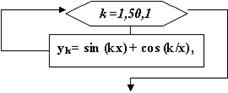
Цикл
На блок-схеме изображена алгоритмическая структура типа