Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Раздел 3. Дифференциальные уравнения
|
|
Для самостоятельной подготовки к экзамену (зачету, тесту) по
Математике, 2 семестр для студентов дневной и заочной (полной и
Сокращенной) форм обучения инженерно-технических и экономических специальностей
Раздел 1. Определенный интеграл
1. Вычислить определенный интеграл, применяя подходящую подстановку.
1.1. 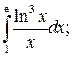 1.2.
1.2. 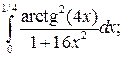 1.3.
1.3. 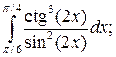 1.4.
1.4. 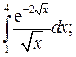
1.5. 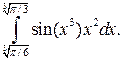
2. Вычислить площадь плоской области 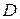 , ограниченной данными линиями. Построить область
, ограниченной данными линиями. Построить область 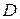 .
.
2.1. 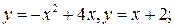 2.2.
2.2.  2.3.
2.3. 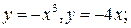
2.4. 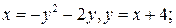 2.5.
2.5. 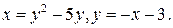
Раздел 2. Функции нескольких переменных
3. Найти частные производные  функции двух переменных
функции двух переменных 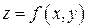 и записать ее полный дифференциал.
и записать ее полный дифференциал.
3.1.  3.2.
3.2. 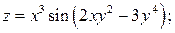 3.3.
3.3. 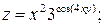
3.4. 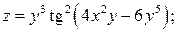 3.5.
3.5. 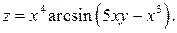
Раздел 3. Дифференциальные уравнения
4. Найти частное решение (или частный интеграл) дифференциального уравнения первого порядка, удовлетворяющее заданному начальному условию (решить задачу Коши).
4.1. 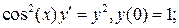 4.2.
4.2. 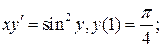 4.3.
4.3. 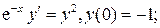
4.4. 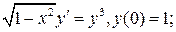 4.5.
4.5. 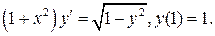
5. Найти частное решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям (решить задачу Коши).
5.1. 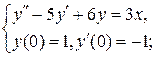 5.2.
5.2. 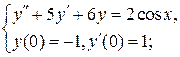 5.3.
5.3. 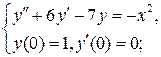
5.4. 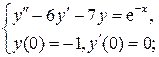 5.5.
5.5.