Понятие градиента. Планирование и организация эксперимента

Планирование и организация эксперимента

Практические занятия

ОБЩИЕ УКАЗАНИЯ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ

В процессе изучения дисциплины «Планирование и организация эксперимента» каждый студент должен выполнить отчет по практическим занятиям.

Практическое занятие состоит из общей методики и решения практической задачи.

Каждый студент выполняет практические занятия самостоятельно в соответствии с индивидуальным заданием (вариантом, который соответствует номеру по списку), используя данные методические указания, учебники, учебные пособия, справочники, ГОСТы и др.

Отчет по практическим занятиям должен быть представлен одним файлом. Все листы, кроме титульного, нумеруются. Титульный лист оформляется по форме, образец которого представлен на странице кафедры АТСиП во вкладке «Учебная литература».

Изложение практического занятия должно быть кратким, логич-ным, четким, призванным дать обоснование принятым решениям. Со-кращение слов в тексте не допускается. Значение символов и числовых коэффициентов, входящих в формулы, должны быть приведены непосредственно под формулой.

Практические занятия, выполненные не по вариантам и не по установленной форме, к защите не принимаются.

Тема. ГРАДИЕНТНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ

Понятие градиента

Любую совокупность вещественных чисел (v ₁, v ₂, …, v_k), взятых в определенном порядке, можно рассматривать как точку или вектор с теми же координатами в пространстве k измерений (k -мерном пространстве). Запись вида v = (v ₁, v ₂, …, v_k) обозначает точку или вектор v с указанными в скобках координатами [4]. Если для k -мерных векторов v и w справедливы основные алгебраические операции:

сложение и вычитание

v ± w = (v ₁ ± w ₁, v ₂ ± w ₂, …, v_k ± w_k),

умножение на действительное число u

u × v = (u × v ₁, u× v ₂, …, u × v_k),

скалярное произведение

v × w = (v ₁ × w ₁, v ₂ × w ₂, …, v_k × w_k),

то совокупность всех таких векторов называют k -мерным евклидовым пространством и обозначают E_k.

Длиной вектора v называют число, определяемое по формуле

.

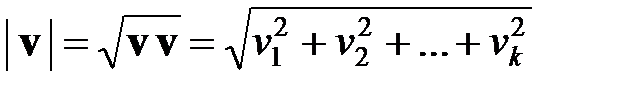(1.1)

Длину вектора можно вычислить только тогда, когда компоненты вектора представлены в одной шкале измерений или они являются безразмерными величинами, полученными, например, в результате преобразования (1.1) – кодированные переменные безразмерны.

Если произведение v × w = 0 при | v | ≠ 0 и | w | ≠ 0, то векторы v и w являются ортогональными.

Единичным называют вектор, определяемый по формуле

.

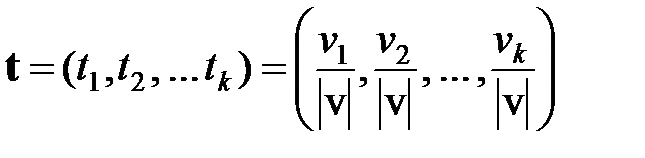(1.2)

Пусть в E_k заданы некоторая точка V = (v ₁, v ₂, …, v_k), единичный вектор t и непрерывно дифференцируемая по всем аргументам функция f (V) = f (v ₁, v ₂, …, v_k). Производной в точке V от функции f (V) по направлению луча, определяемому вектором t, называется предел

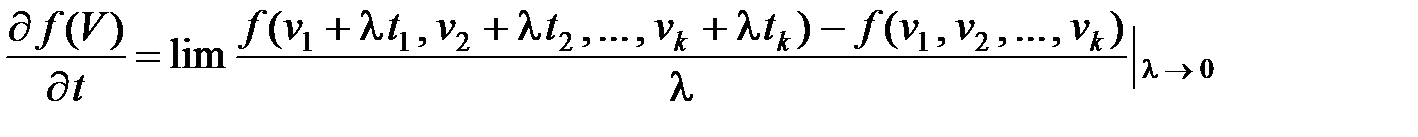или

.

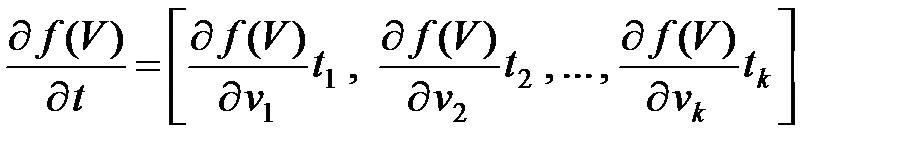Градиентом функции f (V) называют вектор Ñ f (V) с координатами, равными частным производным по соответствующим аргументам

.

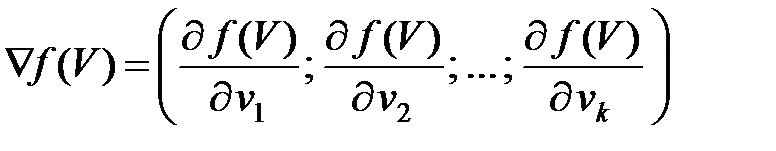(1.3)

Градиент указывает направление наибольшего возрастания функции. Противоположное направление –Ñ f (V) называется антиградиентом, оно показывает направление наискорейшего убывания функции. В точке экстремума V^* градиент равен нулю Ñ f (V^* ) = 0. Если аналитически производные определить невозможно, их вычисляют приближенно ¶ f (V) / ¶ v_i» D f (V) / D v_i, где D f (V) – приращение функции f (V) при изменении аргумента на величину D v_i. Двигаясь по градиенту (антиградиенту) можно достичь максимума (минимума) функции. В этом и состоит сущность градиентного метода оптимизации.