Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Силы давления покоящейся жидкости на цилиндрические стенки
|
|
Рассмотрим часть твёрдой цилиндрической поверхности, назовём её цилиндрической стенкой. Пусть стенка находится под односторонним воздействием давления покоящейся жидкости.
Разобьём стенку на элементарные площадки. В силу малости площадок будем считать их плоскими. Элементарные силы давления на них dP=pdω.
Силы dP не параллельны друг другу, их линии действия могут не пересекаться в одной точке. Определим силу избыточного давления.
Цилиндрическая поверхность с горизонтальной образующей. Направим ось 0Y параллельно образующей (рис. 2.9), а ось 0Z – вертикально вверх. Сила давления на цилиндрическую поверхность
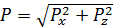, (2.40)
где Px и Pz – горизонтальная и вертикальная составляющие силы давления.
Выделим на цилиндрической поверхности элементарную площадку dω, на которую действует направленная по нормали элементарная сила dP=ρ ghdω. Её горизонтальная и вертикальная составляющие:
;
.
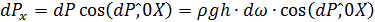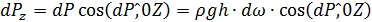Учитывая, что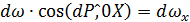 
и 
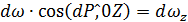(где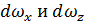 
- проекции площадки dω на плоскости, нормальные к осям 0X и 0Z), найдём, что
; 
.
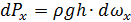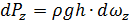Проинтегрировав, получим для горизонтальной составляющей силы P:
, (2.41)
где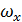 
- проекция всей цилиндрической поверхности на плоскость, нормальную к оси 0X; 
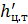- глубина центра тяжести проекции 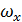под пьезометрической плоскостью (свободной поверхностью).
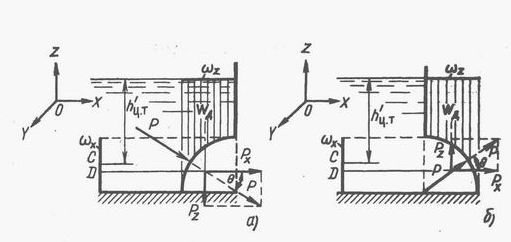Рис. 2.9
|
.
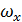Расстояние от свободной поверхности до центра давления
.
Для вертикальной составляющей
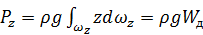. (2.42)
Интеграл в (2.42) выражает объём призмы, ограниченной снизу цилиндрической поверхностью, а сверху - её проекцией ω z напьезометрическую плоскость. Образующие призмы - вертикальные прямые. Полученную таким образом фигуру называют телом давления.
Вертикальная составляющая Pz численно равна весу жидкости в объёме W д тела давления.
На схеме а рис. 2.9 сила Pz направлена вниз, на схеме б – вверх.
Линию действия P определяют направляющие косинусы:
; 
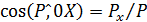. (2.43)
Некоторые примеры к определению силы Pz приведены на рис. 2.10.
Рис. 2.10
|
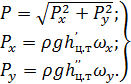(2.44)
Линию действия силы P определяют направляющие косинусы
; 
.
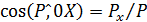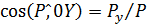Для цилиндрической поверхности в виде четверти поверхности цилиндра радиусом r и высотой h с вертикальной образующей (рис. 2.11):
; 
; 
; 
.
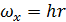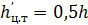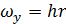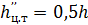Круглая труба с вертикальной осью заполнена покоящейся жидкостью под постоянным давлением (рис. 2.12). Найдём силу, действующую на стенки трубы. Горизонтальная сила Px, стремящаяся разорвать трубу длиной l по вертикальному диаметральному сечению при давлении p, равна
.
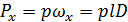Эта сила действует на трубу как растягивающая. Она уравновешивается силами сопротивления, возникающими в материале трубы.
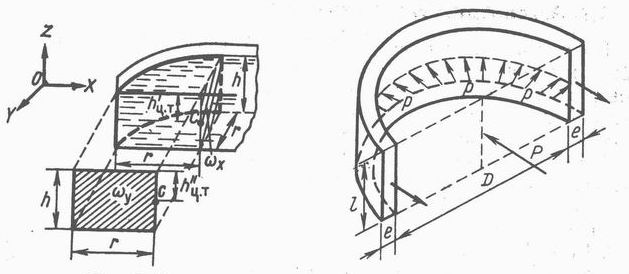Рис. 2.11 Рис. 2.12
|
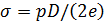. (2.45)
Произвольная криволинейная стенка abcd (рис. 2.13). В этом случае составляющие силы P по направлениям горизонтальных осей 0X и 0Y (Px и Py) и вертикальной оси 0Z (Pz) не равны нулю:
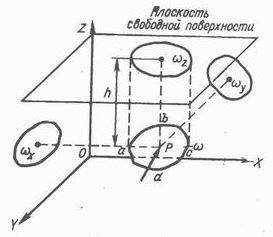Рис. 2.13
|
(2.47)
Если линии действия составляю-щих пересекаются, то воздействие жид-кости сводится к одной силе P. Линию действия силы P определяют углы между направлением P и координатными осями. Косинусы этих углов
;
;
.
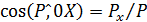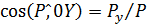Литература по содержанию лекции:
1. Чугаев Р. Р. Гидравлика (Техническая механика жидкости). - Л.: Энергоиздат, 1982. - 672 с.
2. Штеренлихт Д. В. Гидравлика. - М.: Энергоатомиздат, 1985. - 640 с.
3. Гиргидов А. Д. Механика жидкости и газа (гидравлика): Учебник для вузов. СПб: Изд-во СПбГПУ, 2002. - 545 с.