
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
в, г, д,
|
|
А б
Дано геод корд Q1(B; L) линия S2; А1-2. Треб-ся опр широту и долготу (.) Q2; обр азимут А2-1. такая задача наз прямой геод задачей. В практике геод работ возник др задача: по данным геод корд-м Q1 b Q2 вычисл расс-е м-у пунктами-обр геод задача. Дано(B1 L1)Q1 (B2 L2)Q2 A1-2 и А2-1 S1-2
Прямая геод задача реш-ся гл образом при вычислении геод корд-т. в результате вычис-я будут известны все длины сторон
Для нач пункта (1) изв-ы (B0 L0) и азимут А0 на один из пунктов, зная корд нач пункта, расстояние и азимут на соседние пункты. Мат методы обеспеч вычисл с любой точностью Чем выше точность, тем больше осложнения в вычисл-х. в любых вычисл-х след уст точность. На вычисл-я оказ влияние 3 вида ошибок: 1)ошибки исх данных 2)ошибки в формулах 3) ошибки в вычисл-х из-за округл чисел. Наивысшую точность дает триангул 1 кл.ср кв погрешность должна быть 0, 7'' относ-я ср кВ погрешность измер сторон не превыш 1/400000. Длины сторон триангул 1 кл не должны быть больше 20 км.
13 в Стороны триангул 1 кл имеют длину не менее 20 км и не более 60 км, притаких малых S для реш-я прямой геод задачи можно найти простые ф-ы, кот-е прим-ся для реш геод корд-т и азимутов пунктов триангул 3 кл.
В полярн сфероидич треуг PQ2Q1 из (.) Q2 провед-м линию Q2Q0 под прямым углом.Угол t необх для получ-я обр азимута А21. т о мы получим 2 прямоуг сфероидич треуг, из кот-х треуг Q0Q1Q2 все стороны < 60 км. (.) Q0 наз вспомог (.) введение этой (.) в значит мере облегчает. Послед-ть: реш малый сфероидич треуг, с целью опр длин сторон Q1Q0=b Q0Q2=c после этого по длине дуги меридиана Δ х=bнах-м разность широт B0-B1 м/у (.) Q0 Q1 затем реш-ся прямоуг сфероидич треуг Q0BQ2 с целью опр разности долгот l=L2-L1и разности широт м/у (.) Q0 Q2 d=Q0-Q2 и ∟ t. Этот ∟ t представл азимут нап-я провед-го из (.) Q2 в линии Q0Q2. Здесь малыми величинами будут дуги l, В, С. Взяв в кач-е радиуса сферы ср радиус кривизны зем эллипсоида R1= корень из M1N1 реш малым треуг Q1Q2 как сферич-й по сп аддитаментов, т е
14 а. Конеч практич цель триангуляционных и полигонометрических работ — опр полож геод пунктов на поверхности принятого референц-эллипсоида. Полож-е этих пунктов можно опр в различных системах координат. Необходимо вычис корд пунктов в такой системе, которая была бы проста и обеспечивала бы наиболее удобное и легкое использование координат в разнообразных практических целях. Такой системой является система плоских прямоугольных координат. В этой системе вычис коорд пунктов съемочного обоснования, для которых координаты триангуляционных пунктов являются исходными, производят различного рода расчеты при проектировании и строительстве разнообразных инженерных сооружений и перенос проектов в натуру. Использов-е топогр планов существенно облегчается, если на них нанесена сетка координатных линий в прямоугольной плоской системе координат. Прямоугольные координаты геодезических пунктов необходимы при использовании геодезических данных для оборонных целей.Система геод координат имеет ряд достоинств; она наиболее удобна для решения научных задач высшей геодезии и в этой системе координат обычно обрабатывают триангуляцию 1 класса, однако она неудобна для широкого использования в указанных практических целях. Действительно, взаимное положение пунктов в этой системе определяется в угловых единицах (градусах, минутах и секундах широты и долготы), причем линейное значение этих единиц различно в зависимости от широты места; направления меридианов, от которых отсчитываются азимуты, не параллельны между собой; вычисления при помощи геодезических координат, даже при малых расстояниях, сложны, трудоемки и требуют известной подготовки вычислителя.
Т.о, для практич использов наиб удобна система плоских прямоугольных координат.
14 б. Известно, что поверхность эллипсоида не может быть развернута на плоскость без искажений, поэтому и не может быть предложена система плоских прямоугольных координат, в которой без искажений было бы выражено взаимное положение точек земной поверхности.
Поставленная задача сводится к изображению поверхности эллипсоида на плоскости по некоторому определенному закону. Математически такой закон (или проекция) в общем виде может быть выражен уравнениями
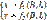
В этих уравнениях х и у — плоские прямоугольные координаты изображаемой на плоскости точки, выраженные как функции геодезических координат той же точки на поверхности эллипсоида. Если выбрать под тем или иным условием закон изображения точек эллипсоида на плоскости, то можно, пользуясь написанными формулами, получить формулы для перехода от расстояний и углов на поверхности эллипсоида к соответствующим расстояниям и углам на плоскости.
14 в Чтобы получить топографич планы в единой системе. Требов-я кот-е след поставить при выбореф-ии f1 f2:
1. min-е искажение изобр-х на пл-и эл-в поверхности эллипсоида. 2. легкость и простота учета этих искаж-й. 3)простота и легкость прим-я проекций и учета искажений, важный показатель достоинства проекции.
14 г поправки за искажение должны выч-ся с ошибками в 5-10 р < ошибок непосред-х изм-й. при выборе проекции след стрем-ся к мин-му числу зон на территор данного гос-а. проекция должна обеспеч-ть переод из одной зоны в др. Проекцию предложил Гаусс а Крюгер разработал детали ф-ы и дал раб ф-ы. При использов проекции Г-К эллипсоид разд-ся на зоны меридианами. Каждая зона представл собой сфероидич от одн полюса до др огранич мер-м. l0-ср меридиан
14 д Осн усл и св-ва конфорного изобр: 1)∞ малый контур на эл-е изобр подобен ему на пл-и. 2) угл-е искажение отсутствует. 3) М изобр-я в каждой (.) зависит от направл-я.
15а. Систему прямоугольных координат Гаусса — Крюгера ввели в СССР в 1930 г. В связи с увеличением объема топографо-геодезических работ возникла необходимость иметь координаты опорной геодезической сети в прямоугольной системе, причем единообразно выбранной. Плоские прямоугольные координаты применялись и до указанного времени; в землеустройстве — координаты Зольднера при частных началах координат в различных районах; в крупных маркшейдерских геодезических сетях — свои системы координат при самостоятельно выбранных началах. Естественно, такой разнобой в применении системы плоских прямоугольных координат затруднял использование материалов топографо-геодезических работ в общих целях, создавал неудобства при смыкании съемок на граничных линиях районов, имеющих свои системы координат, вызывал необходимость различного рода перевычислений.
В связи с этим третье геодезическое совещание при Госплане СССР в 1928 г. вынесло решение о необходимости введения системы координат Гаусса — Крюгера, установило шестиградусную ширину зон по долготе, определило положение осевых меридианов каждой зоны (как это указано выше) и наметило мероприятия для введения новой системы координат.
В 1930 г. были изданы составленные под руководством Ф. Н. Красовского «Руководство, формулы и таблицы по применению прямоугольных координат Гаусса — Крюгера», что и способствовало введению этой системы координат в практику геодезических работ. После этого координаты Гаусса — Крюгера получили в СССР всеобщее распространение, и в настоящее время во всех каталогах геодезических пунктов обязательно помещают плоские прямоугольные координаты в этой системе.
Искажение длин на краю шестиградусной зоны может достигать величины
порядка  —
— 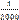 поэтому при топографических съемках мелкого и среднего масштабов — 1: 100 000, 1: 50 000 — эти искажения во взаимном положении точек при съемках не ощущаются. Учитывать эти искажения необходимо при постановке топографических работ указанных масштабов лишь при развитии съемочного обоснования в виде малых триангуляции, теодолитных ходов и т. п. Измеренные длины линий исправляют путем введения поправок, выбираемых из специальных таблиц.
поэтому при топографических съемках мелкого и среднего масштабов — 1: 100 000, 1: 50 000 — эти искажения во взаимном положении точек при съемках не ощущаются. Учитывать эти искажения необходимо при постановке топографических работ указанных масштабов лишь при развитии съемочного обоснования в виде малых триангуляции, теодолитных ходов и т. п. Измеренные длины линий исправляют путем введения поправок, выбираемых из специальных таблиц.
При крупномасштабных съемках, если они к тому же производятся не графическим, а числовым методом, в пределах небольших участков изменение масштаба становится заметным и его нельзя считать постоянным даже при небольших расстояниях (20—50 км) от осевого меридиана. При проектировании по карте или перенесении проектов в натуру графическая точность масштаба карты и установленные допуски требуют учета размеров искажения. Значительно больший объем непосредственных измерений, требующих учета искажений с большой точностью, не позволяет применять шестиградусную зону для съемок крупного масштаба без того, чтобы не осложнить производство съемок.
А
Основные формулы
а) Перейдем к выводу основных формул проекции Гаусса — Крюгера. Задача заключается в определении функций f1 и f2 из уравнений
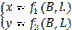
Исходные условия для получения этих функций: а) конформность проекции, б) выбор зон и осей координат описанным выше способом, в) изображение осевого меридиана и экватора на плоскости прямыми линиями, г) масштаб изображения по осевому меридиану равен единице.
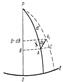
16 б. Пусть на рисунке ОЕ — экватор эллипсоида, а РО — осевой меридиан. Дана точка А, имеющая геодезические координаты — широту В и долготу L; точка А1 расположена на бесконечно малом расстоянии от точки А в произвольном направлении от нее; координатами точки А1 будут В + dB и L + dl. Через X назовем длину дуги осевого меридиана от экватора до параллели с широтой В. Пусть прямые Ох и Оy — ось абсцисс и ось ординат соответственно, расположенные перпендикулярно одна к другой, суть изображения экватора и осевого меридиана на плоскости. Пусть точка а — изображение на плоскости точки А; точка а1, находящаяся на бесконечно малом расстоянии от точки а, соответствует точке А1 Обозначим прямоугольные координаты точки а на плоскости через х и y, а точки а1 — через х + dx и у + dy. Обозначим расстояние АА1 на эллипсоиде через ds, а расстояние аа1 на плоскости — через dS. Построим вспомогательный треугольник АА1С и будем рассматривать его как элементарный, тогда найдем, что А1С равно элементу дуги меридиана MdB, АС — элементу дуги параллели N cos Bdl. Отсюда
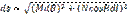
Или
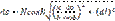
Введем обозначение
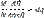
Тогда
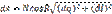
Для плоскости
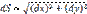
Масштаб изображения выразится так:
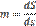
Или
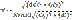
Перепишем уравнение в виде
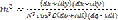
Где 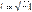
Уравнение выражает масштаб изображения для произвольного закона изображения. Для обеспечения конформности изображения масштаб т по всем направлениям должен быть одинаков и зависеть только от координат данной точки, но не от направления элемента ds. Следовательно, вид функции, определяющий зависимость между координатами на плоскости и геодезическими координатами на эллипсоиде, должен быть таков, чтобы выражение
(37.6) для масштаба не зависело от отношения дифференциалов 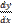 или
или 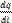
которые определяют направление отрезков 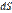 или
или 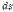
В теории функции комплексного переменного доказывается, что P+iQ только тогда является аналитической функцией комплексного переменного p+iq, когда 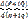 не зависит от
не зависит от 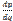 ; наоборот, чтобы
; наоборот, чтобы 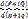 не зависело от
не зависело от 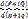 , необходимо, чтобы P+iQ было аналитической функцией комплексного переменного p+iq Имея это в виду, переписываем уравнение так:
, необходимо, чтобы P+iQ было аналитической функцией комплексного переменного p+iq Имея это в виду, переписываем уравнение так:
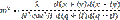
Согласно изложенному выше свойству функций комплексного переменного, для того чтобы масштаб изображения не зависел от направления отрезка ds
или от 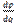 необходимо, чтобы
необходимо, чтобы 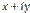 было некоторой аналитической функцией
было некоторой аналитической функцией
 от
от 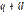 или
или 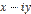 — аналитической функцией от
— аналитической функцией от 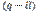 , т. е. чтобы
, т. е. чтобы 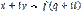
в, г, д,
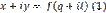
Справедливость и достаточность последнего условия можно еще доказать следующим образом.
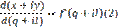
Заменив в (1) +i на –i получим:

И
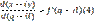
Следовательно, выражение (4) имеет место, если поставлено условие (1). На основании формул (2) и (4) выражение  примет вид
примет вид
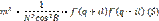
Производные 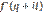 и
и 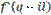 при наличии условий (1) и (3)
при наличии условий (1) и (3)
зависят только от координат x, y или q, l, но не зависят от их дифференциалов, поэтому не зависят от них и выражения (5) и 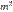 , что и требовалось доказать.
, что и требовалось доказать.
Условие (1) обеспечит конформность изображения при любом произвольном виде аналитической функции f
Для получения конформного изображения эллипсоида на плоскости по Гауссу вид функции f определяют путем введения следующих дополнительных условий:
1) осевой меридиан ОР эллипсоида изображается на плоскости прямой, являющейся осью абсцисс; следовательно, в уравнении (1) при l = 0 ординаты у должны быть равны нулю;
2) для точек осевого меридиана абсциссы х должны быть равны соответствующим дугам X, т. е. дугам меридиана от экватора до данной точки с широтой В.
Отсюда в уравнении (1) при y=0
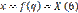
Разложим f(q + il) в ряд Тейлора, предполагая, что величина il сравнительно невелика. Будем иметь
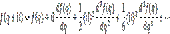
или
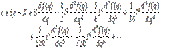
Производные в этом ряде должны быть вычислены при l=0, вследствие
чего они обращаются в производные 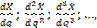
поэтому
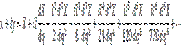
Приравнивая порознь действительные и мнимые части в полученном выражении, находим в общем виде основные уравнения, определяющие закон изображения точек эллипсоида на плоскости в проекции Гаусса:
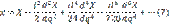
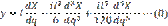
Очевидно, чем больше l, тем больше должно быть удержано членов в уравнениях (7) и (8), т. е. чем больше будут искажения на краях зоны, тем учет этих искажений сложнее.
Как указывалось выше, в настоящее время наибольшая протяженность зон по долготе принята 6°. Таким образом, удаление пунктов от осевого меридиана по долготе не превосходит 3°, поэтому последующие рабочие формулы для вычислений при применении проекции Гаусса — Крюгера и рассчитаны на интервал в долготе l  3°.
3°.
24. Уравнения поправок измеренной стороны
а) два определяемых пункта:
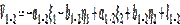
б) исходный пункт и определяемый:
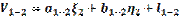
в) два исходных пункта:
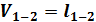
20. Преобразование координат Гаусса — Крюгера из одной зоны в другую
На практике нередко возникает задача перевычисления (преобразования) координат из одной зоны в другую. Эта задача заключается в том, что координаты какого-либо пункта или многих пунктов, отнесенные к осевому меридиану с долготой L'o одной зоны, требуется перевычислить с отнесением к осевому меридиану другой зоны, имеющему долготу L" o. Такая задача может возникать в следующих случаях:
1) если триангуляционная сеть расположена на стыке двух смежных зон (исходные данные в восточной и западной частях триангуляции отнесены к разным осевым меридианам этих зон), то для уравнивания такой триангуляции в системе одной зоны необходимо преобразовать координаты исходных пунктов из одной зоны в другую;
2) в связи с переходом на систему трехградусных зон в районах, где намечено исполнение топографических съемок в крупных масштабах (1: 10 000, 1: 5000), при наличии координат опорной сети, вычисленных в шестиградусной зоне, возникает задача перевычисления координат из шестиградусных зон в трехградусные или в зону с частным значением долготы осевого меридиана;
3) при обработке ходов съемочного обоснования аэрофотосъемки на границе зон необходимо координаты опорных пунктов государственной триангуляции иметь в одной системе; если эти пункты расположены в разных зонах и координаты их отнесены к разным осевым меридианам, то возникает необходимость перевычисления координат из одной зоны в другую;
4) если выполнены съемочные работы для составления специальных крупномасштабных планов и район работ оказался на стыке двух зон, или даже в одной зоне, но на ее краю, то возникает необходимость перевычисления координат имеющихся опорных пунктов при некотором другом осевом меридиане, проходящем через территорию данной съемки. Это оказывается необходимым в связи с недопустимой величиной искажений на краю зоны при использовании в специальных целях съемочных материалов.
При окончательном вычислении координат пунктов государственной триангуляции и составлении каталогов принято за правило проводить «перекрытие» зон, т. е. для точек, лежащих вблизи раздельного меридиана, давать координаты в двух смежных зонах. Эта мера в значительной степени приводит к сокращению случаев необходимости преобразования координат пунктов из одной зоны в другую, но не исключает их.
|