
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Системы счисления
|
|
Системы счисления – принятый способ наименования и записи чисел с помощью символов, имеющих определенные количественные значения.
Все системы счисления можно разделить на два класса: позиционные и непозиционные. В позиционной системе счисления количественное значение каждой цифры зависит от ее места (позиции) в числе. В непозиционных системах счисления значение цифры не зависит от места, которое он занимает в числе. Самый известный пример – римская система счисления. В этой системе счисления используется 7 знаков
I (1) V (5) X (10) L (50) C (100) D(500) M(1000)
Например, III (три) LIX (59) DLV (555)
Для записи чисел в различных системах счисления используется некоторое количество отличных друг от друга знаков. Число таких знаков в позиционной системе счисления называется основанием системы счисления.
Некоторые системы счисления
| Основание | Системы счисления | Знаки |
| Двоичная | 0, 1 | |
| Пятеричная | 0, 1, 2, 3, 4 | |
| Восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 | |
| Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | |
| Шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д. Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения
an-1 qn-1 + an-2 qn-2+... + a1 q1 + a0 q0 + a-1 q-1 +... + a-m q-m,
где ai – цифры системы счисления; n и m – число целых и дробных разрядов, соответственно.
Например:
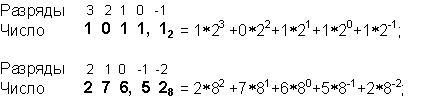
692(10) = 6*102 + 9*101 + 2*100
1101(2) = 1*23 + 1*22 + 0*21 + 1*20 = 13(10)
112(3) = 1*32 + 1*31 + 2*30 = 14(10)
341, 5(8) = 3*82 + 4*81 + 1*80 + 5*8-1 = 225, 125(10)
A1F, 4(16) = A*162 + 1*161 + F*160 + 4*16-1 = 2591, 06(10)
Если в приведенных выше примерах произвести арифметические действия в правой части равенства, то получится число в десятичной системе счисления. Это и есть способ перевода из любой системы счисления в десятичную.