Опис лабораторного обладнання

Теоретичні відомості

Властивості RC-фільтрів обумовлені залежністю від частоти ємнісного опору конденсаторів. Вони характеризуються простотою конструкції, малою вартістю, нечутливістю до магнітних полів, можливістю побудови малогабаритних схем для найнижчих частот тільки за рахунок збільшення номіналів резисторів.

Фільтр нижніх частот (ФНЧ) є схемою, яка без змін передає сигнали нижніх частот, а на верхніх частотах забезпечує затухання сигналів і запізнення їх за фазою відносно вхідних сигналів. На рис. 2.1 наведена схема простого RC-фільтра нижніх частот.

Рис. 2.1 – Простий ФНЧ

Для розрахунку частотної характеристики схеми використаємо формулу відношення напруг, представлених в комплексній формі:

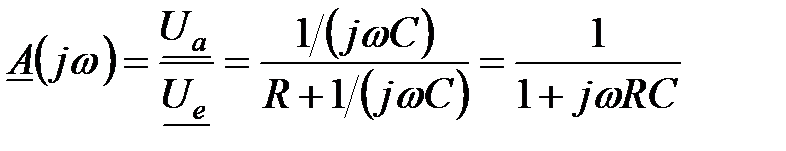. (2.1)

З виразу (2.1), враховуючи, що 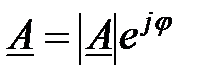, отримаємо

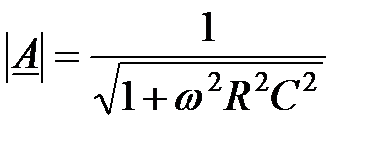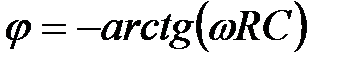; . (2.2)

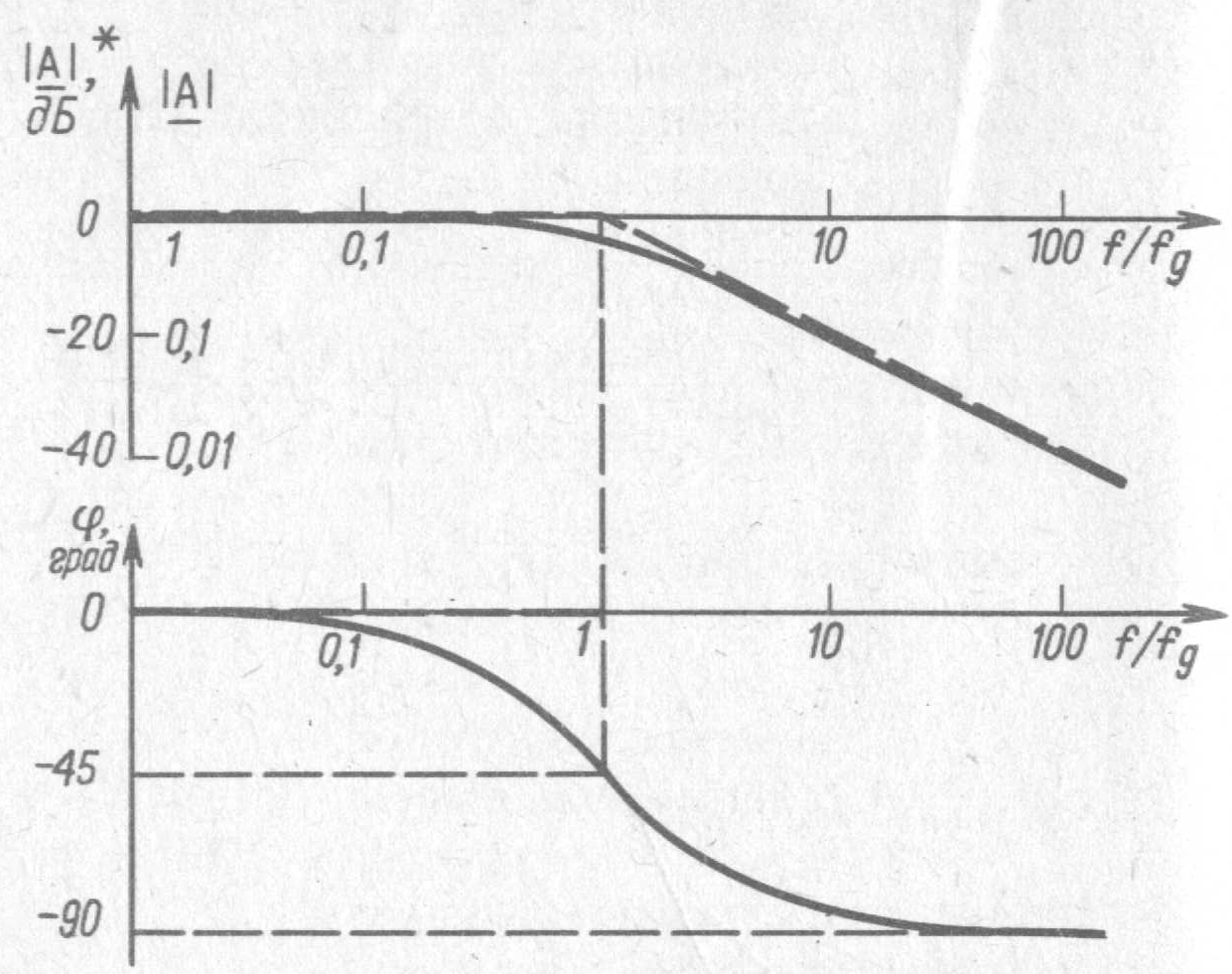
Залежності, що описуються формулою (2.2) представлені на рис. 2.2.

Рис. 2.2 – Діаграма Боде для ФНЧ

Підставивши 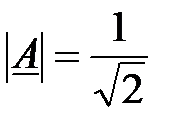, отримаємо вираз для визначення частоти зрізу

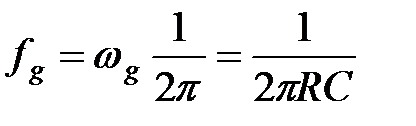. (2.3)

Фазовий зсув j на такій частоті, відповідно до формули (2.2), складає –45°.

Як видно з рис. 2.2, амплітудно-частотну характеристику 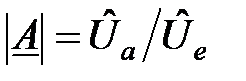найпростіше скласти з двох асимптот:

1) 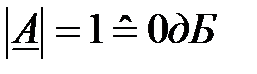на нижніх частотах f < < f_g;

2) на високих частотах f > > f_g, відповідно до формули (2.2), 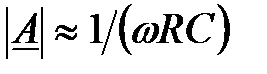, тобто коефіцієнт підсилення обернено пропорційний частоті. При збільшенні частоти в 10 раз коефіцієнт підсилення зменшується в 10 раз (зменшується та 20 дБ на декаду або на 6 дБ на октаву);

3) 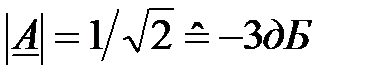при f = f_g.

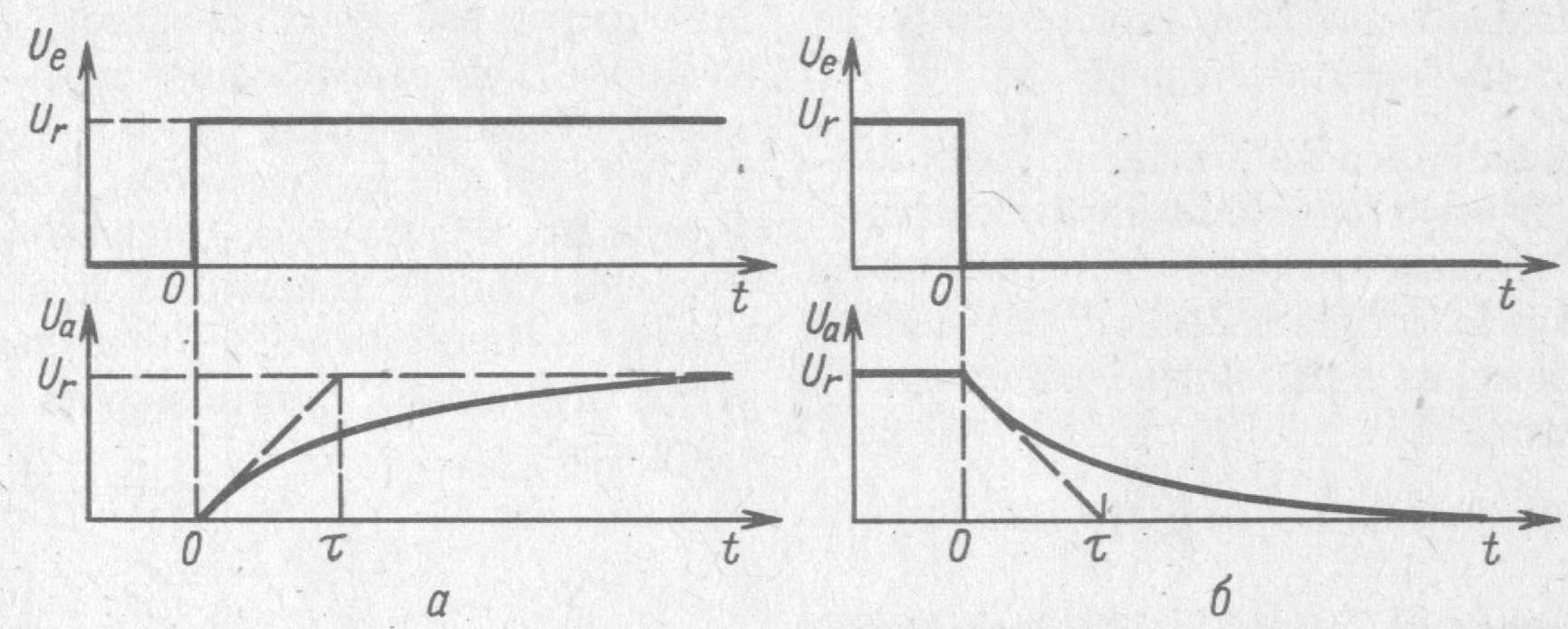
Для аналізу схеми в часовій області на вхід схеми (рис. 2.1) подається імпульс напруги (рис 2.3).

Рис. 2.3 – Реакція ФНЧ на скачок напруги

Щоб розрахувати вхідну напругу, використовується правило вузлів до ненавантаженого виходу. Тоді для схеми, що зображена на рис 2.1, запишемо

.

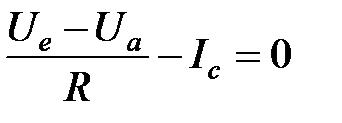Враховуючи, що 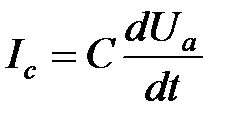отримаємо диференціальне рівняння

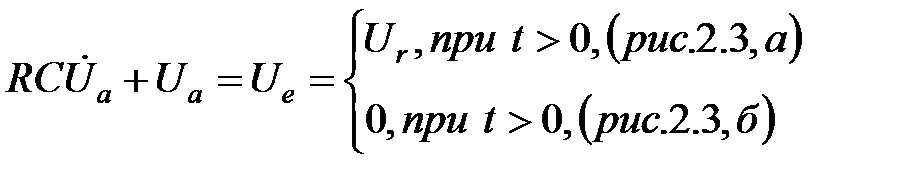. (2.4)

Диференціальне рівняння (2.4) має таке рішення:

- для рис. 2.3, а: ;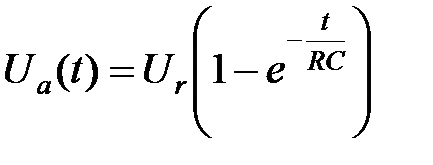

- для рис. 2.3, б: 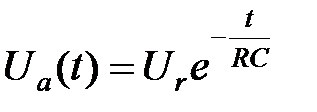. (2.5)

Відомо, що до установившихся значень U_a=U_r i U_a=0 криві будуть наближатися асимптотично. Тому в якості міри часу установки вихідної напруги прийнята постійна часу t. Вона показує інтервал часу, протягом якого процес досягає значення, що відрізняється від установившогося на 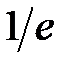частину величини стрибка напруги на вході. З формули (2.5) видно, що постійна часу дорівнює

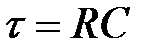. (2.6)

Іншим параметром, що характеризує ФНЧ, є тривалість інтервалу фронта імпульсу. Цей параметр показує час, на протязі якого вихідна напруга зростає від 10 до 90 % кінцевого значення, якщо на вхід подати імпульс напруги прямокутної форми. Враховуючи властивості експоненціальної функції, з формул (2.5) отримаємо

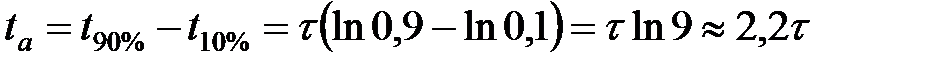. (2.7)

При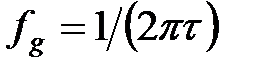

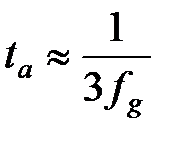. (2.8)

Це співвідношення з високою ступіню точності дійсне для ФНЧ.

При послідовному зєднанні декількох ФНЧ, що забезпечують різні тривалості фронта вихідного імпульсу t_ai, результуюча тривалість фронта імпульсу дорівнює

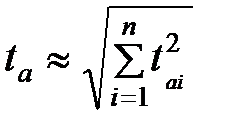. (2.9)

Частота зрізу наближено визначається так

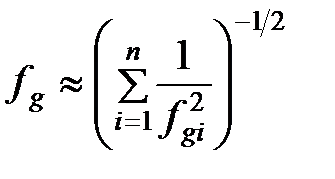. (2.10)

Для випадку з n фільтрами із рівними частотами зрізу

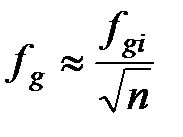. (2.11)

Фільтр верхніх частот (ФВЧ) – це схема, яка передає без змін сигнали високих частот, а на низьких частотах забезпечує затухання сигналів і випередження їх за фазою відносно вхідних сигналів. Схема простого RC-фільтра верхніх частот наведена на рис. 2.4.

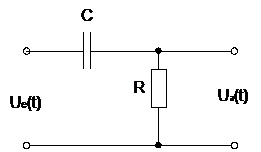
Рис. 2.4 – Простий RC-фільтр верхніх частот

Амплітудно-частотні і фазочастотні характеристики отримаємо з формули для відношення напруг

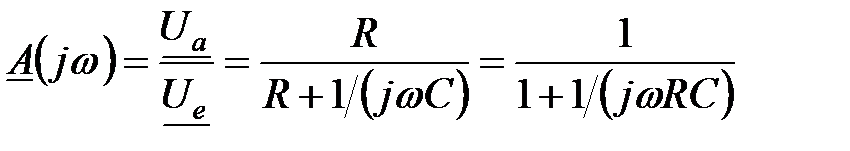. (2.12)

З виразу (2.12) визначається

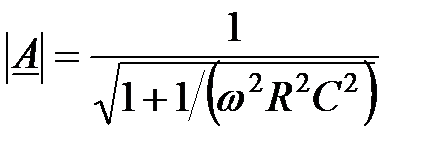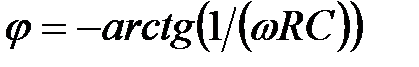; . (2.13)

Вираз для частоти зрізу співпадає з відповідним виразом для ФНЧ

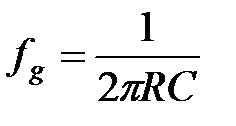. (2.14)

Фазовий зсув на цій частоті складає +45°. Як і для ФНЧ, найпростіше скласти АЧХ в подвійному логарифмічному масштабі за допомогою асимптот:

1) 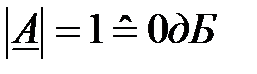на високих частотах f > > f_g;

2) на низьких частотах f < < f_g, відповідно до формули (2.13), 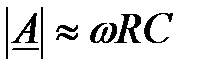, тобто коефіцієнт підсилення пропорційний частоті. Нахил асимптоти дорівнює +20 дБ на декаду або +6дБ на октаву.

3) При f = f_g, як і для ФНЧ

.

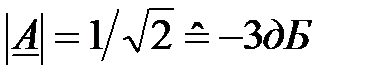В результаті розрахунку реакції на імпульс напруги, постійна часу, як і для ФНЧ, дорівнює t=RC.

При послідовному з’єднанні ФВЧ результуюча частота зрізу визначається з виразу

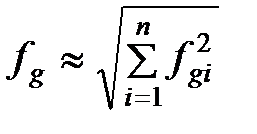. (2.15)

Для випадку з n фільтрів із рівними частотами зрізу

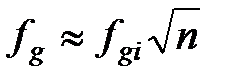. (2.16)

Опис лабораторного обладнання

Для експериментальних досліджень роботи RC-фільтрів використовується програма ElectronicsWorkbench, MicroCap або Proteus при побудові основних схем ввімкнення RC-фільтрів верхніх та нижніх частот. В цих програмних середовищах необхідно промоделювати роботу RC-фільтрів, схеми яких наведено в табл. 2.1. При моделюванні схем фільтрації на вхід фільтрів необхідно подавати гармонічні сигнали за допомогою генератора напруги з амплітудою 1, 5 В та несучою частотою для ФНЧ – 600 Гц, а для ФВЧ – 10 кГц. Для дослідження основних характеристик RC-фільтрів до виходу необхідно підключити вбудований осцилограф та аналізатор АЧХ і ФЧХ.

Таблиця 2.1

Тип фільтра	Назва	Схема
	ФНЧ	Одно-ланковий
2	ФНЧ	Двох-ланковий
	ФНЧ	Трох-ланковий
	ФВЧ	Одно-ланковий
	ФВЧ	Двох-ланковий
	ФВЧ	Трох-ланковий