
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Мастер функций f(х), Статистические, ЛИНЕЙН
|
|
Задание 1
Рассмотреть способы построения уравнения парной регрессии, вычисления прогноза и оценки его точности на основе следующего примера:
Имеются данные по 50 предприятиям о стоимости основных производственных фондов (ОПФ) (х, млн р.) и среднесуточной производительности (у, т) в таблице 1.
Таблица 1
| № | ||||||||||||
| х | 35, 03 | 36, 79 | 37, 40 | 36, 68 | 37, 62 | 38, 48 | 39, 09 | 39, 23 | 39, 26 | 39, 31 | 39, 72 | 40, 19 |
| у | 12, 98 | 15, 35 | 15, 81 | 17, 13 | 18, 64 | 18, 6 | 24, 29 | 23, 41 | 22, 21 | 19, 80 | 21, 84 | 17, 53 |
| № | ||||||||||||
| х | 40, 10 | 40, 19 | 40, 41 | 40, 76 | 41, 54 | 41, 68 | 45, 12 | 48, 42 | 48, 29 | 48, 65 | 51, 93 | 53, 23 |
| у | 16, 29 | 22, 13 | 19, 81 | 21, 30 | 20, 18 | 24, 17 | 24, 97 | 26, 44 | 24, 19 | 22, 05 | 22, 16 | 27, 72 |
| № | ||||||||||||
| х | 54, 35 | 54, 69 | 56, 61 | 56, 76 | 56, 80 | 57, 30 | 59, 26 | 59, 84 | 61, 45 | 61, 72 | 62, 91 | 65, 21 |
| у | 25, 86 | 21, 15 | 25, 37 | 24, 83 | 30, 80 | 28, 00 | 30, 55 | 31, 66 | 29, 77 | 31, 12 | 35, 13 | 33, 73 |
| № | ||||||||||||
| х | 67, 92 | 67, 63 | 68, 45 | 68, 24 | 68, 46 | 68, 58 | 68, 53 | 69, 17 | 69, 45 | 70, 98 | 71, 4 | 74, 23 |
| у | 29, 08 | 32, 66 | 34, 12 | 33, 88 | 26, 33 | 34, 54 | 36, 34 | 29, 19 | 28, 50 | 35, 60 | 32, 19 | 30, 76 |
| № | ||||||||||||
| х | 74, 97 | 75, 78 | ||||||||||
| у | 31, 87 | 38, 00 |
Парный регрессионный анализ начинается с построения уравнения регрессии 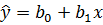 . Получить его можно двумя способами:
. Получить его можно двумя способами:
Первый способ. Построение линейной регрессии с помощью:
Мастер функций f(х), Статистические, ЛИНЕЙН
Порядок действий следующий.
1. Введите исходные данные в ячейки А1: В51 (таблица 1).
2. Выделите область пустых ячеек 5x2 (5 строк, 2 столбца) D2: E6 для вывода результатов регрессионной статистики или область 1x2 - для получения только оценок коэффициентов регрессии.
3. Активируйте Мастер функций любым из способов:
а) в главном меню выберите Вставка/Функция;
б) на панели инструментов Стандартная щелкните по кнопке
Вставка функции.
4. В окне «Категория» (рис. 1) выберите Статистические, в окне «Функция» - ЛИНЕЙН. Щелкните по кнопке ОК.
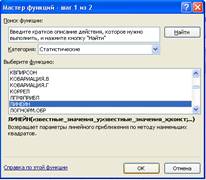
Рис.1 Диалоговое окно «Мастер функций»
5. Заполните аргументы функции (рис. 2)

Рис.2 Диалоговое окно ввода аргументов функции ЛИНЕЙН
Известные_значения_ y - диапазон, содержащий данные ре-зультативного признака (среднесуточной производительности).
Известные_значения _ x - диапазон, содержащий данные факторов независимого признака (стоимости ОПФ).
Константа — логическое значение, которое указывает на наличие или отсутствие свободного члена в уравнении. Если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0.
Статистика — логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щелкните по кнопке ОК.
6. В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу F2, а затем на комбинацию клавиш CTRL+SHIFT+ENTER. Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме (таблица 2):
Таблица 2
Значение коэффициента 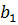
| Значение коэффициента 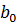
|
Среднеквадратическое отклонение коэффициента 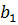
| Среднеквадратическое отклонение коэффициента 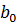
|
Коэффициент детерминации 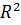
| Стандартная ошибка регрессии 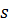
|
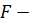 статистика статистика
| Число степеней свободы 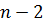
|
| Объясненная регрессией сумма квадратов отклонений RSS | Остаточная сумма квадратов ESS |
Получить результат для данных из рассматриваемого примера (таблица 1)
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, описывающий полученную прямую, уравнение которой можно записать в виде:
________________________________
Свободный член экономического значения не имеет, в отличие от коэффициента регрессии, который показывает, что ____________________________________________________________________________________________________________________________________
Второй способ. Построение линейной регрессии
с помощью инструментов Сервис, Анализ данных, Регрессия
С помощью инструмента параметров Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа и доверительных интервалов, а также остатки и графики подбора линии регрессии.
Порядок действий следующий.
1. Активируйте доступ к Пакету анализа (если он не был активирован до этого). В главном меню последовательно выберите Сервис, Надстройки. Установите флажок Пакет анализа (рис. 3).
2. В главном меню выберите Сервис, Анализ данных, Регрессия. Щелкните по кнопке ОК.
3. Заполните диалоговое окно ввода данных и параметров вывода (рис. 4):
Входной интервал y, x - аналогичны известным значениям y ($B$2: $B$51), x ($A$2: $A$51).
Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет

Рис. 3 Подключение надстройки Пакет анализа
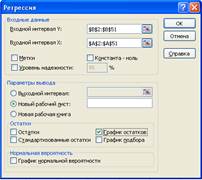
Рис. 4. Диалоговое окно ввода параметров инструмента Регрессия
Константа-ноль — флажок, указывающий на отсутствие свободного члена в уравнении.
Выходной интервал — достаточно указать левую верхнюю ячейку будущего диапазона.
Новый рабочий лист — можно задать произвольное имя нового листа.
Если необходимо получить информацию об остатках и их графиках, установите соответствующие флажки в диалоговом окне.
Щелкните по кнопке ОК.
Получить результаты регрессионного анализа для данных из примера.