Определение локального экстремума функции двух переменных.

Функция 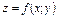имеет локальный максимум в точке М₀(х₀, у₀), если значении функции в этой точке больше, чем её значение в любой другой точке М(х, у) некоторой окрестности точки М_0. (т.е. М₀ – максимум, если 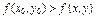для любых точек её окрестности.)

Функция 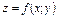имеет локальный минимум в точке М₀(х₀, у₀), если значении функции в этой точке меньше, чем её значение в любой другой точке М(х, у) некоторой окрестности точки М₀ (Точка М₀ – минимум, если 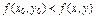для любых точек её окрестности.)

Условия существования экстремума для функции двух переменных.

Необходимое: Если функция 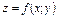достигает экстремума при х=х₀, у=у₀, то каждая частная производная первого порядка от этой функции при этих значениях аргументов или обращается в ноль или не существует.

Достаточное: Пусть в некоторой окрестности точки М₀(х₀, у₀) функция 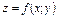имеет непрерывные частные производные, равные нулю в этой точке, тогда, если 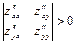, М₀(х₀, у₀) – является экстремумом функции ,

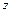причём, если 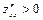, точка М₀ – минимум, если 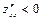, точка М₀ – максимум.

Производная неявной функции: 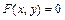, тогда

Определение производной по направлению заданного вектора. Производная функции 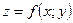, в данном направлении 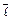, равна пределу отношения приращения функции в этом направлении к величине перемещения, при стремлении последнего к нулю.

Формула производной по направлению.

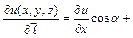
, где - направляющие косинусы вектора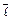

Вектор градиент. Вектор, координаты которого равны частным производным функции 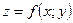, называется вектором градиентом этой функции. .

Признак дифференцируемости функции двух переменных в точке.

Если функция 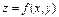имеет непрерывные частные производные в точке , то она дифференцируема в этой точке.

Полным дифференциалом функции 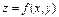называется главная, линейная часть полного приращения , вычисленная по формуле: , где дифференциалы независимых переменных совпадают с их приращениями ().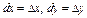

Признак полного дифференциала.

Выражение 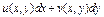является полным дифференциалом некоторой функции 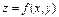в области D, если функции и и их частные производные непрерывны в этой области и 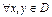выполняется

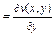
Использование полного дифференциала в приближенных вычислениях

ПРИМЕР. Найти полный дифференциал и полное приращение функции 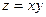в точке М(4; 5) при 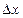= 0, 1; = 0, 2.

=

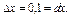
Формула для вычисления приближенного значения функции.

+ +

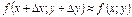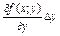
Частные производные сложной функции.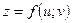

;

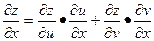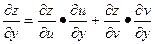
Формула для вычисления полной производной сложной функции.

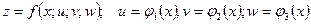
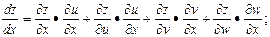
Формула для вычисления полного дифференциала сложной функции.

, тогда d z =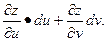