
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические сведения. Исследование свойств отношений
|
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 4.
Исследование свойств отношений. Алгоритм вычисления транзитивного замыкания отношения R на множестве М
(алгоритм Уоршалла)
Цель занятия: Изучение алгоритма вычисления транзитивного замыкания отношения R на множестве М (алгоритм Уоршалла).
Теоретические сведения.
Пример 1. Дано отношение, заданное матрицей
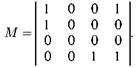
Исследовать отношение на
1. симметрию,
2. антисимметрию,
3. асимметрию,
4. рефлексивность,
5. антирефлексивность.
Найти транзитивное замыкание отношения. Построить граф отношения ρ и его транзитивного замыкания.
Решение
Исследуем свойства данного отношения.
1) Данное отношение не является симметричным, так как матрица несимметрична. Например, пара (2, 1) принадлежит ρ, а пара (1, 2) ему не принадлежит.
2) Отношение антисимметрично, так как нет ни одной пары m ij = mji = 1, i=j.
3) Отношение антисимметрично, но не асимметрично, так как на диагонали матрицы имеются элементы равные 1.
4) Все диагональные элементы матрицы рефлексивного отношения равны
1. Данное отношение не является рефлексивным.
5) Отношение не обладает свойством антирефлексивности, так как диагональ матрицы ненулевая.
Найдем транзитивное замыкание ρ.



3. Элемент m43 = 1. Дизъюнкция четвертой и третьей строки не меняет вид матрицы. Таким образом полученная матрица является матрицей транзитивного замыкания отношения ρ.
Оба способа дают один и тот же результат.
На рис. 1 и рис. 2 представлены графы отношения ρ и его транзитивного замыкания. Диагональные элементы матрицы соответствуют петлям на графе. Матрица несимметричная, поэтому граф отношения ориентированный.
Пример 2. Пусть бинарное отношение R на M задано в виде диаграммы, состоящей из узлов и стрелок так, что узлам взаимно однозначно соответствуют элементы множества М, а стрелкам, соединяющим пару а и b в направлении от а к b, - наличие отношения a R b. Определить графические особенности диаграммы в зависимости от характера свойств отношения R.
1. Отношение R 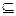 M
M  M рефлексивно, если a R а для любых а
M рефлексивно, если a R а для любых а  М. Соответствующая диаграмма рефлексивного отношения должна содержать петли во всех узлах (т.е. стрелки, начинающиеся и заканчивающиеся в одном узле).
М. Соответствующая диаграмма рефлексивного отношения должна содержать петли во всех узлах (т.е. стрелки, начинающиеся и заканчивающиеся в одном узле).
2. Отношение R антирефлексивно, если ни для каких а  М не выполняется a R а. Диаграмма антирефлексивного отношения не должна содержать ни одной петли.
М не выполняется a R а. Диаграмма антирефлексивного отношения не должна содержать ни одной петли.
3. Отношение R симметрично, если из a R b следует b R а. В диаграмме симметричного отношения для каждой стрелки, соединяющей два узла, существует также стрелка, соединяющая эти узлы в обратном направлении.
4. Отношение R антисимметрично, если из aRb и bRa следует а = b. В диаграмме антисимметричного отношения не существует двух различных узлов, связанных парой (разнонаправленных) стрелок.
5. Отношение R транзитивно, если из aRb и bRc следует aRс. В диаграмме транзитивного отношения для любых двух стрелок таких, что одна направлена от а к b, а другая – от b к с, существует стрелка, соединяющая а и с в направлении от а к с.
Пример 3. Каковы свойства отношений, заданных:
1. На множестве натуральных чисел N:
а) R 1 – " быть не больше 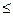 ";
";
б) R 2– " быть делителем";
в) R 3 – " быть равным".
2. На множестве точек действительной плоскости 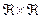 :
:
а) R 4–" находиться на одинаковом расстоянии от начала координат";
б) R 5–" быть симметричным относительно оси X " '.
3. На системе множеств 2М:
a) R 6 - " пересекаться с" (иметь непустое пересечение);
b) R 7 – " являться строгим включением с".
4. На множестве людей:
а) R 8– " быть сыном";
б) R 9– " жить в одном городе";
в) R 10–" быть братом".
5. На множестве элементов структуры (рис. 3):
а) R 11–" быть непосредственно связанным с";
б) R 12–" быть начальником".
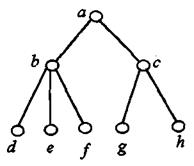
Рис. 3.
|