Вычислительная сложность метода Холесского

В общем случае перестановки при решении СЛАУ с разреженной матрицей определяются в процессе компромисса между требованиями устойчивости алгоритма (перестановки строк и столбцов матрицы СЛАУ в ходе выбора главного элемента в методе Гаусса) и желанием учета разреженности матрицы (желанием уменьшить заполнение матрицы в процессе исключения). Однако алгоритм Холесского для СЛАУ с симметричной положительно определенной матрицей не требует перестановок для поддержания устойчивости алгоритма (не требует выбора главного элемента). Матрицу СЛАУ в этом случае можно переупорядочить еще до начала реального численного разложения. Выбранная структура хранения матрицы при ее разложении остается статичной. Таким образом, три задачи

1. Выбор надлежащего упорядочения СЛАУ;
2. Формирование подходящей схемы хранения для матрицы СЛАУ (этот вопрос обсуждается в последующих лекциях)4
3. Реальное вычисление

могут быть разделены как самостоятельные объекты исследования и как разные модули программного обеспечения.

Теорема. Число операций, необходимых для вычисления треугольного множителя Холесского симметричной положительно определенной матрицы 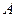, равно

,

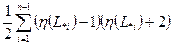где 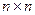- размер матрицы СЛАУ, 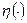- количество ненулевых элементов в аргументе, 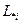- i- ый столбец матрицы .

Таким образом, вычислительная сложность алгоритма Холесского зависит от количества ненулевых элементов в треугольном множителе Холесского , т.е. чем меньше ненулевых элементов (чем меньше заполнений при исключении) в матрице , тем меньше вычислительная сложность алгоритма Холесского. Таким образом, решение задачи уменьшения заполнения матрицы в процессе разложения путем переупорядочения является актуальной.