Понятие ленты матрицы. Ленточный метод хранения разреженной матрицы

Понятие основной и накладной памяти

Понятие ленты матрицы. Ленточный метод хранения разреженной матрицы

Понятие оболочки матрицы. Профильный метод хранения разреженной матрицы.

Преимущества и недостатки различных схем хранения матриц.

Понятие основной и накладной памяти

Память, используемая для хранения разреженных матриц, обычно состоит из двух частей: основной памяти, содержащей числовые значения, и накладной памяти, где хранятся указатели, индексы и другая информация, нужная для запоминания структуры матрицы и облегчения доступа к числовым значениям. Поскольку за машинную память приходится платить независимо от того, как она используется, всякая оценка запросов к памяти для данного метода решения должна включать описание способа, которым будет храниться матрица или матрицы, так чтобы в этой оценке накладная память могла быть учтена наряду с основной.

Сравнение двух различных стратегий с точки зрения критерия памяти может сводиться к сравнению существенно различных структур данных, имеющих весьма различающуюся накладную память. Поэтому метод, предпочтительный в смысле величины основной памяти, может уступать конкуренту, если в сравнении учитывается и накладная память. Эта ситуация проиллюстрирована на рис.1.

Рис.1.

Понятие ленты матрицы. Ленточный метод хранения разреженной матрицы

Пусть 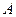- симметричная матрица с элементами . Для 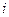-ой строки 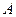, , 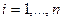обозначим:

, .

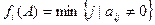Число 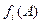- это столбцовый индекс первого ненулевого элемента 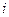-ой строки 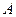. Если предположить, что матрица 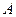еще и положительно определенная, то ее диагональные элементы 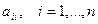, положительны, и

.

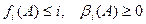Определим ширину ленты матрицы 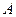следующим образом:

.

Число 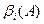называется 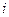-ой шириной ленты 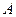. Лента определяется следующим образом:

,

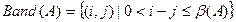т.е. это область матрицы, удаленная от главной диагонали не более, чем на 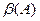позиций.

Пример. Матрица на рис.2 (ненулевые элементы обозначены звездочками) имеет ширину ленты, равную трем.

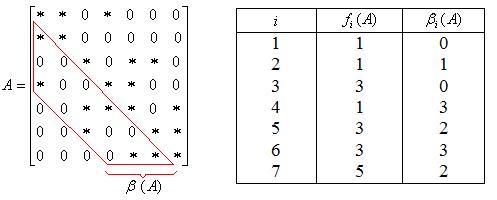
Рис.2.

Матрица с шириной ленты, равной единице, называется трехдиагональной.

Применение ленточного метода подразумевает, что нули вне 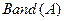игнорируются; нули же внутри ленты обычно хранятся. Использование разреженности здесь основано на соотношении:

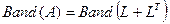, (10)

где 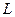- нижний треугольный множитель Холесского в разложении 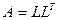. Действительно, как следует из (10), если при разложении матрицы 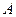возникнут заполнения, то они могут возникнуть только всередине ленты, а нули нижнего (верхнего) треугольника матрицы 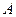вне ленты останутся нулями в нижнем (верхнем) треугольнике 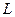(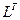), т.е. нули вне ленты можно не хранить.

Исходя из вышесказанного, обычным методом хранения симметричной ленточной матрицы 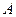является так называемая диагональная схема хранения. Поддиагонали нижнего треугольника 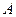, составляющие 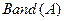, вместе с главной диагональю хранятся по столбцам в прямоугольном массиве с размерами 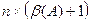(пример представлен на рис.3).

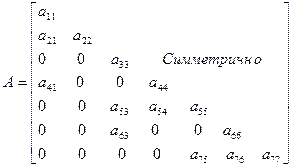
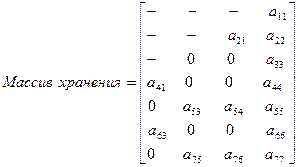
Рис.3.