Обратный алгоритм Катхилла-Макки упорядочения вершин графа

Построение графа, отвечающего разреженной матрице

Обратный алгоритм Катхилла-Макки упорядочения вершин графа

Периферийные и псевдопериферийные узлы графа. Понятие корневой структуры уровней.

Алгоритм поиска псевдопериферийных узлов графа

Упорядочение Кинга

Обратный алгоритм Катхилла-Макки упорядочения вершин графа

Одним из наиболее широко используемых алгоритмов упорядочения симметричной разреженной матрицы, имеющих целью уменьшение ширины ленты, является метод Катхилла-Макки. Этот метод работает непосредственно с графом, отвечающим матрице.

В основе метода Катхилла-Макки лежит следующее очень наглядное и простое замечание, которое проиллюстрировано на рис.1. Пусть 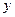— помеченный узел графа, отвечающего 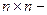матрице 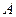, а 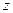— непомеченный узел, смежный с 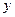. Для того, чтобы уменьшить ширину ленты в строке, соответствующей 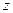, нужно присвоить 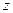номер, как можно менее отличающийся от номера .

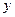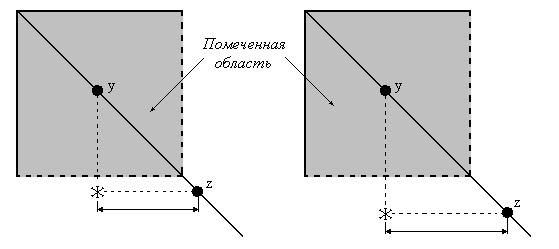
Рис.1. Влияние на ширину ленты нумерации смежных узлов

Схема Катхилла-Макии — это метод уменьшения ширины ленты матрицы посредством локальной минимизации чисел 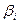, определенных в лекции 11. Это приводит к предположению, что схему можно использовать и для уменьшения профиля 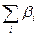матрицы. Практически было обнаружено, что упорядочение, получаемое обращением упорядочения Катхилла-Макки, часто гораздо сильнее уменьшает профиль, чем первоначальное упорядочение, хотя ширина ленты остается неизменной. Это упорядочение называется обратным упорядочением Катхилла-Макки (RCM). Можно доказать, что обратная схема всегда не хуже прямой в отношении хранения и обработки оболочки.

Для связного графа алгоритм RCM можно описать следующим образом (вопрос о выборе начального узла на шаге 1 рассматривается ниже).

Шаг 1. Определить начальный узел 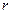и выполнить присваивание

,

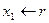т.е. узел 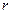получает метку 1.

Шаг 2. Для 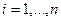найти всех ненумерованных соседей узла 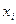и занумеровать их в порядке возрастания степеней.

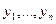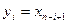Шаг 3 (обратное упорядочение). Обратное упорядочение Катхилла-Макки есть , где для .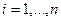

В случае, если граф несвязен, описанный алгоритм можно применять к каждой связной компоненте графа по очереди.

Пример. Рассмотрим применение алгоритма RCM к графу на рис.2.

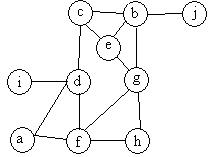
Рис.2.

Предположим, что в качестве начального взят узел 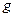. В табл.1 показано, как нумеруются узлы на шаге 2 алгоритма.

Таблица 1 –

Номер	Узел	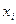Ненумерованные соседи в порядке возрастания степеней
		- - - - -

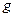
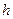
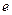
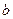
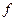
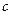
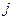
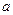
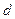
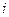
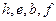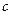
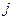
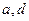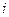Обратное упорядочение Катхилла-Макии приведено на рис.3. Размер оболочки равен 22.

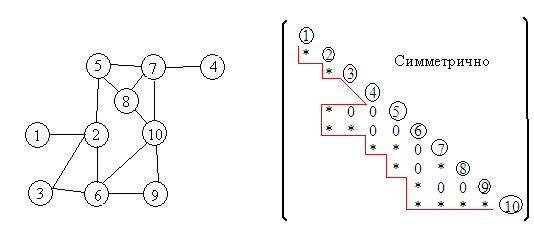
Рис.3.

Эффективность алгоритма упорядочения критическим образом зависит от выбора начального узла. Если в нашем примере в качестве начального взять узел «a», то получим меньший профиль, равный 18 (рис.4).

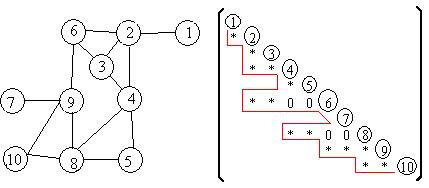
Рис.4.

Установим теперь грубую оценку сложности алгоритма RCM, считая, что начальный узл задан. Под операцией понимается сравнение либо выборка элемента информации из структуры смежности, применяемой для хранения графа.

Теорема. Если для сортировки, проводимой в ходе работы алгоритма Катхилла-Макки, используется метод пузырька, то временная сложность RCM ограничена величиной 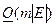, где 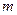— максимальная степень узла, а 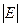— мощность множества ребер графа.