Степенной метод нахождения максимального по модулю собственного значения. Область применимости степенного метода

Лекция 24. Проблема вычисления максимального и минимального по модулю собственного значения матрицы

План

Степенной метод нахождения максимального по модулю собственного значения. Область применимости степенного метода

Метод обратной итерации нахождения минимального по модулю собственного значения. Условия целесообразности его использования

Нахождение наименьшего собственного значения положительно определенной матрицы

Степенной метод нахождения максимального по модулю собственного значения. Область применимости степенного метода

Предположим, что квадратная -матрица 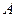имеет полную систему нормированных собственных векторов :

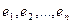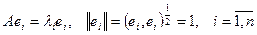, (1)

где 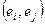- скалярное произведение в 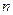-мерном евклидовом пространстве, 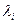- собственное значение матрицы 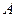, которое соответствует собственному вектору .

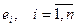Предположим, что

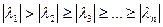, (2)

т.е. существует единственное собственное значение, максимальное по модулю.

Возьмем произвольно вектор 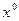и построим векторную последовательность 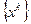по рекурентным соотношениям:

.

Разложим вектор 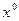по собственному базису :

.

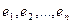Учитывая, что

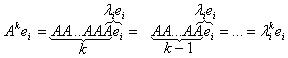
получим:

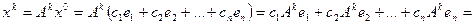
(3)

Из (3) вытекает, что

.

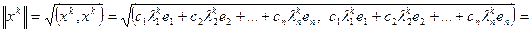
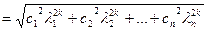Рассмотрим векторную последовательность 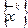, элементы которой определяются согласно формуле:

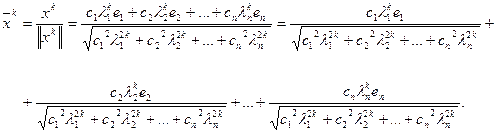(4)

Из предположения (2) вытекает, что при 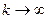все слагаемые в правой части (4), кроме первого, стремятся к нулю, а первый

.

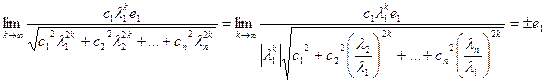Таким образом

,

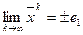т.е. последовательность 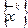стремится при 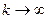к собственному вектору матрицы 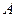, который отвечает максимальному по модулю собственному значению 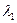. Кроме того

.

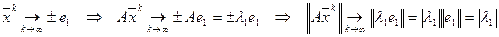Таким образом

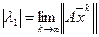. (5)

Такой метод нахождения максимального по модулю собственного значения и соответствующего собственного вектора называется степенным методом или методом итераций, который пошагово выглядит следующим образом:

Шаг 1. Выбрать произвольно 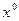(на практике 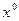выбирается так, чтобы ).

Шаг 2. Для 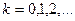делать:

а) ;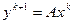

б) ;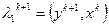

в) ;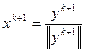

г) сравнить 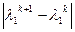с заданной погрешностью вычислений.

Для реализации этого метода достаточно в памяти ЭВМ хранить матрицу 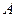, два вектора 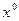, 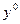и два приближения 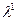и 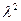к максимальному по модулю собственному значению. В этом случае алгоритм можно записать следующим образом:

Шаг 1. Задать точность вычисления 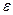и начальное приближение к максимальному по модулю собственному значению ;

Шаг 2. Выбрать вектор ();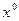

Шаг 3. Сделать:

а) , = ;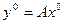

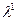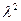б) ;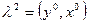

в) ;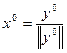

г) если ,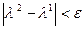

то 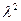- искомое собственное значение, 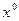- соответствующий собственный вектор,

иначе перейти на шаг 3.

Главным преимуществом степенного метода является то, что в нем не надо делать никаких преобразований матрицы 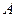. Каждый шаг этого метода требует 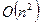арифметических операций для этапа 3(а), 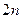операций для этапа 3(б), - на этапе 3(в).

Главным недостатком степенного метода является то, что он может очень медленно сходиться, а в случае, когда матрица 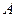имеет несколько собственных значений с максимальным модулем, метод вообще расходится.