Метод решения задачи Коши, основанный на разложении решения в ряд Тейлора

Лекция 33.Численные методы решения задачи Коши

План

Задача Коши. Одношаговые и многошаговые методы решения задачи Коши

Метод решения задачи Коши, основанный на разложении решения в ряд Тейлора

1. Задача Коши. Одношаговые и многошаговые методы решения задачи Коши

Обыкновенное дифференциальное уравнение первого порядка можно записать в виде:

.

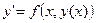Это уравнение имеет бесконечное множество решений (если имеет решение вообще) 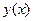. Например, если 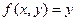, то решением уравнения 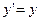будет бесконечн много функций вида: 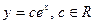. Если в некоторой точке 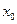задать значение 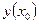, то мы получим единственное решение. Такая задача, определяющая единственное решение дифференциального уравнения,

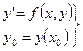(1)

называется задачей Коши.

Только некоторые дифференциальные уравнения могут быть решены аналитически. Чаще решения дифференциальных уравнений – единственное решение задачи Коши для этих уравнений, приближают при помощи численных методов.

Будем рассматривать пошаговые методы. Для решения задачи (1) на отрезке 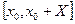генерируется последовательность точек 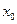, ,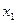..., , 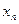принадлежащих 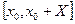, возможно с переменной длиной шага 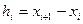, и в каждой точке значение 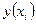приближается некоторым числом . Если вычисляется только при помощи 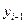, то такие методы называются одношаговые; если вычисляется по значениям 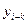,..., , 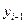то такие методы называются многошаговые.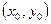

1. Метод решения задачи Коши, основанный на разложении решения в ряд Тейлора

Одним из методов решения задачи Коши является метод, основанный на разложении решения вряд Тейлора.

Пусть на 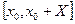необходимо решить задачу (1). Возьмем производную от уравнения 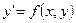, присутствующего в (1), по :

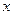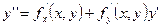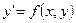, . (10)

(Например, если 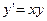, то 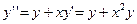). Дальше можно найти 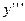, дифференцируя полученное равенство (10), аналогично 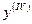и т.д. Подставляя 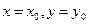, получим:

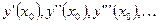
Тогда возможно приблизить значение 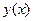усеченной суммой соответствующего ряда Тейлора, построенного с центром в точке :

,

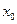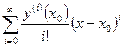т.е.

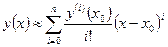(2)

Однако, если 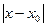больше радиуса сходимости ряда 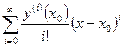, то погрешность формулы (2) не стремится к 0. В этом случае сегмент 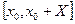разбивают на части 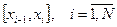. Будем последовательно получать приближения к значениям :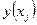

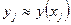
следующим образом. Если уже найдено, мы вычисляем 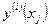и тогда приближение функции 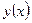в точке 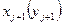вычисляются по формуле:

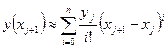, (3)

в предположении, что область сходимости соответствующего ряда включает в себя отрезок 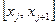.