Класс вычислительных формул решения задачи Коши, основанных на квадратурных формулах численного интегрирования

Рассмотрим другой класс вычислительных формул. Пусть известно значение 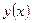. Нужно вычислить 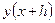. Имеет место следующее тождество:

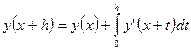(5)

Вычислим 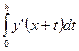по квадратурной формуле левых прямоугольников:

.

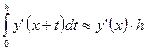Тогда

,

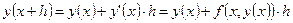т.е. получили формулу Ейлера.

Для получения более точного приближения необходимо в правой части (5) использовать более точную формулу численного интегрирования.

Воспользуемся, например, квадратурной формулой трапеции:

.

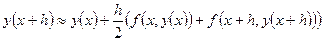Тогда соответствующая вычислительная формула будет такой:

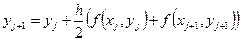. (6)

Полученная формула более точная, чем формула Эйлера. Однако, в общем случае (6) может быть неразрешимой относиельно . Поэтому в правой части вместо используют некоторое его приближение: возможно вычислить, например, по формуле Эйлера:

,

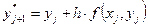а затем уточнить:

.

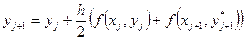Можно воспользоваться в (5) формулой средних прямоугольников:

.

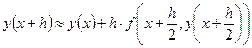Тогда аналогично получим следующие рассчетные формулы:

.
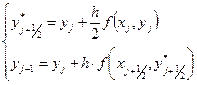