Разделенные разности и их свойства

Обобщением понятия производной является понятие разделенной разности. Разделенные разности нулевого порядка 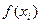просто совпадают со значениями функции 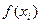; разности первого порядка определяются равенством:

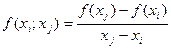. (230)

Если вспомнить определение производной функции в точке :

,

и сравнить с (230), то становится очевидной аналогия разделенной разности с производной.

Разделенные разности второго порядка определяются равенством:

,

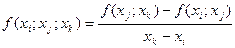и вообще, разности 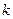-го порядка определяются через разности 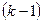-го порядка в соответствии с формулой:

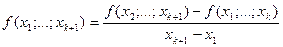. (240)

Лемма. Справедливо равенство:

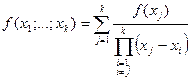. (250)

Доказательство. Для доказательства воспользуемся методом математической индукции. Проверим выполнение (250) для :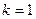

;

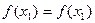для :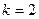

,

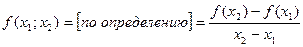а ,

что говорит о выполнении (250) для .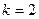

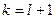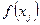Предположим, что для для формула (250) доказана. Покажем, что тогда она верна и для , т.е. , а коэффициент при действительно равен

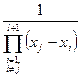. (255)

Для этого преобразуем выражение для 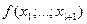, которое получается по определению разделенной разности 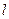-го порядка:

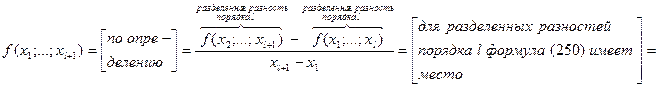
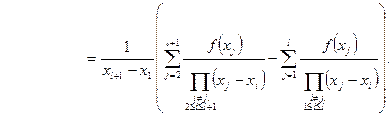(260)

Если , то 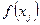присутствует в обеих суммах, стоящих в скобках в правой части формулы (260). Коэффициенты при 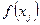в первой и второй суммах соответственно равны:

, .

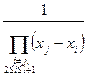Тогда полный коэффициент при 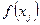в правой части формулы (260) равен:

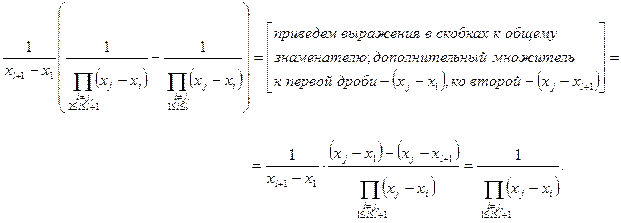
что в точности отвечает (255).

Для или 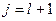значение 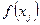входит только в одну сумму в скобках в правой части формулы (260) и коэффициент при нем, как легко убедиться, также имеет требуемый вид (255).

Из предыдущей леммы вытекает, что разделенная разность 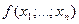является симметрической функцией своих аргументов , т.е. не меняется при любой их перестановке.

Если функция 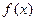задана в точках , то таблицу

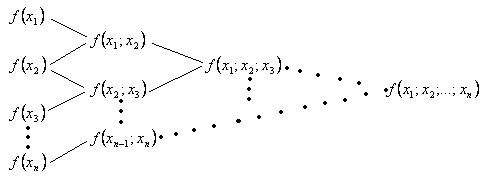
называют таблицей разделенных разностей. Таблица разделенных разностей часто используется для удобства при вычислении значения 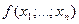, а также всех разделенных разностей меньшего порядка.