
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Властивості пуассоновского потоку
|
|
Імовірність того, що ділянка t виявиться порожнім (не відбудеться жодного події, m=0)
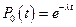
А коли m> t (протилежна подія)
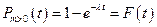 – це функція розподілу.
– це функція розподілу.
Розглянемо випадкову величину (СВ)? проміжок часу між двома сусідніми подіями в найпростішому потоці.
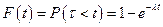 , m=0 – це розподіл проміжку τ, коли туди не попадає жодного події.
, m=0 – це розподіл проміжку τ, коли туди не попадає жодного події.
Якщо ми продифференцируем F(t), то в результаті одержимо щільність розподілу

 Мат очікування СВ t (тобто середній проміжок часу між двома заявками)
Мат очікування СВ t (тобто середній проміжок часу між двома заявками) 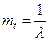 .
.
Середнє квадратичне відхилення від цього середнього 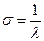
Дисперсія 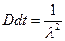
10 Розподіл між проміжками – експонентне (показове).
20 Середньо квадратичне відхилення й мат. очікування будуть рівні 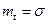
30 Якщо проміжок часу тривав якийсь час τ, те це не впливає на значення розподілу частини, що залишилася, проміжку до появи наступної події. Закон буде таким же, як і для всього проміжку t,
Приклад: автобуси вночі ходять по колу. Ми вийшли в метро й чекаємо автобус. Нехай ми прождали 20 хвилин, і це не виходить, що через 10 хвилин він прийде, якщо автобуси ходять по двох у годину рівномірно (показовий закон).